بسته بندی©
این معما : بازی/ برنده : 16279/24796

 چرا باید این «کمی غذا برای تفکر» را بخوانم ؟
چرا باید این «کمی غذا برای تفکر» را بخوانم ؟
زیرا شما شگفت زده خواهید شد.
 پس از مشاهده و حل چند معما، به نظر شما کدام شاخه از ریاضیات برای حل آنها مفیدتر است :
پس از مشاهده و حل چند معما، به نظر شما کدام شاخه از ریاضیات برای حل آنها مفیدتر است :
1) جبر، 2) نظریه احتمال، 3) هندسه، 4) نظریه اعداد، 5) تقارن، 6) شاخههای دیگر؟
آنچه که به نظر میرسد مفیدتر باشد این است که در مورد بخشپذیری اعداد، به ویژه بخشپذیری بر 2 فکر کنید. این موضوع نظریه اعداد است. چیزهایی که روی هم قرار میدهیم اشیاء هندسی هستند، اما این بدان معنا نیست که دانش هندسی برای حل معماها مورد نیاز است. از هندسه باید بدانیم مساحت یک مربع یا مستطیل چقدر است ، اما نه بیشتر.
برای برخی از معماها، فکر کردن در مورد تقارن نیز بسیار مفید است.
 راهنمای سریع
راهنمای سریع
نکتههایی که در این قسمت بیان میکنیم، برای کسانی است که به دنبال راهنمایی برای انجام بازی هستند اما علاقهای به محتوای ریاضیاتی آن ندارند.
- با نگاه کردن به عددهای ارائه شده در قسمت ( این بازی : برنده/بازی ) که در بالا و سمت چپ هر معما نوشته شده است، بررسی کنید که کدام یک سادهتر هستند. شروع با سادهترین معماها همیشه ایده خوبی است و به شما امکان تمرین با رابط کاربری را میدهد.
- معماهای 2×3×3 شماره 1 و 2×3×3 شماره 2 به راحتی با آزمون و خطا حل میشوند.
- اگر اولین تلاش شما روی معمای 1×7×10 شماره 1 موفقیت آمیز نبود، در تلاش بعدی خود قطعهها را بچرخانید.
- 1×7×7 شماره1 معمایی است که در آن، فکر کردن در مورد تقارن به شما کمک میکند. دلیل آن این است که جعبه(شبکه) دارای یک قاعده مربعی با 4 ضلع مساوی است و ما 4 قطعه بلند مشابه داریم. بنابر این، باید آنها را به صورت متقارن قرار داد. فقط یک قطعه مربعی بنفش وجود دارد. برای داشتن یک جواب متقارن دورانی90 درجه، این قطعه باید در وسط باشد. هر مکان دیگری تقارن 90 درجه جواب را از بین میبرد.
- معماهایی با دکمههای تیرهتر نیاز به تفکر بیشتری دارند. پس از درک کامل معمای 3×3×3 شماره2 به سراغ معماهای 5×5×5 بروید.
 چگونه میتوان این معماها را بدون آزمون و خطا حل کرد ؟
چگونه میتوان این معماها را بدون آزمون و خطا حل کرد ؟
در اینجا چند نکته را بیان میکنیم :
- یک مساله سخت را به موارد سادهتر، یعنی به اهداف سادهتر تقسیم کنید. به عنوان مثال، برای پر کردن کل جعبه، باید هر لایه را پر کرد.
- قطعهها را به صورت متقارن مرتب کنید، به خصوص اگر جعبه متقارن باشد مانند یک مکعب 3×3×3 یا جعبه مربع شکل 1×7×7.
- از اطلاعات داده شده نهایت استفاده را ببرید. اندازه قطعهها چقدر است؟ چه تعداد از آنها شکل یکسانی دارند؟
بقیه این «کمی غذا برای تفکر» با هدف حل همه معماها بدون آزمون و خطا و با مطرح کردن سوالهای ساده و پاسخ دادن به آنها است.
 تعریفها
تعریفها
در اینجا چند اصطلاح وجود دارد که برای بحث در مورد مسالههای بستهبندی از آنها استفاده خواهیم کرد :
 قطعه
قطعه
هر یک از شکلهایی که باید در کنار هم قرار بگیرند تا جسم بزرگتر را بسازند.
یک قطعه فرد قطعهای است که همه طولهای آن فرد باشد، مانند یک قطعه 1×1×1 یا یک قطعه 1×3×5.
یک قطعه زوج قطعهای است که حداقل دو طول زوج داشته باشد، مانند 1×2×4 یا 2×2×2.
 آیا همه قطعهها زوج یا فرد هستند ؟
آیا همه قطعهها زوج یا فرد هستند ؟
خیر. قطعهای با دقیقا یک طول زوج، مانند 1×2×3، با هیچ یک از تعریفها مطابقت ندارد. در بخشهای بعدی بر روی قطعههای فرد و زوج تمرکز خواهیم کرد.
 مکعب مستطیل/جعبه
مکعب مستطیل/جعبه
مکعب مستطیل یک منشور مستطیلی است. برای اشاره به پوسته خالی مکعب مستطیل از کلمه «جعبه» استفاده میکنیم. پس حجم داخلی یک جعبه همان مکعب مستطیل است. در این بازی یک جعبه باید توسط قطعهها پر شود و به کمک قطعهها یک مکعب مستطیل ایجاد شود.
 لایه
لایه
یک برش از یک جعبه به ضخامت 1 در جهت موازی با دو وجه آن را یک لایه مینامیم. یک جعبه 3 ×4 ×5 دارای 3 لایه با اندازه 4 ×5 ، 4 لایه از اندازه 3 ×5 و 5 لایه از اندازه 3 ×4 است.
 یک جعبه 1×5×7 چند لایه دارد ؟
یک جعبه 1×5×7 چند لایه دارد ؟
دارای یک لایه 5 & برابر7 ، پنج لایه 1 & بار7 و هفت لایه 1 & بار5 است. در مجموع دارای 1 + 5 + 7 = 13 لایه است.
 مکعب
مکعب
به طور خاص، یک مکعب 1×1×1، نه یک مکعب بزرگتر. یک قطعه 1×1×1 از 1 مکعب تشکیل شده است، در حالی که یک قطعه 1×1×3 از 3 مکعب تشکیل شده است.
 بلوک ساختمانی
بلوک ساختمانی
چند قطعه متصل به یکدیگر یک بلوک ساختمانی را تشکیل میدهند. بلوکهای ساختمانی جالب یک تقارن خواهند داشت. برای معماهای سختتر، چندین بلوک ساختمانی همنهشت یا همنهشت آیینهای به علاوه یک قطعه مرکزی جعبه را پر میکند.
 استراتژی
استراتژی
نیمی از راه حل یک مساله دشوار، تقسیم آن مساله به مسالههای سادهتر است.
برای انجام این کار، باید سوالهای سادهای از خود بپرسید. سوالهای زیر در حل معماهای بستهبندی مفید خواهد بود.
 آیا میتوان هر مکعب مستطیل را با قطعههایی با اندازه 1×2×2 ساخت؟ به عنوان مثال، آیا میتوان یک مکعب 3×3×3 را تنها با استفاده از قطعههای با اندازه 1×2×2 ساخت؟
آیا میتوان هر مکعب مستطیل را با قطعههایی با اندازه 1×2×2 ساخت؟ به عنوان مثال، آیا میتوان یک مکعب 3×3×3 را تنها با استفاده از قطعههای با اندازه 1×2×2 ساخت؟
نه. یک قطعه 1×2×2 از تعداد زوجی مکعب تشکیل شده است. بنابر این، هر تعداد از قطعههای1×2×2 روی هم تعداد مکعب زوجی خواهند داشت. چون یک مکعب 3×3×3 از تعداد فردی مکعب تشکیل شده است، نمیتوان آن را به این روش ساخت.
در چند بخش بعدی، بررسی خواهیم کرد که چگونه بخشپذیری، به ویژه بر 2، تعیین میکند که برای حل معماهای خاص، قطعهها چگونه باید کنار هم قرار گیرند.
 آیا قطعههای 1 ×2 ×2 میتوانند حداقل هر لایه از جعبه 3×3×3 را پر کنند؟
آیا قطعههای 1 ×2 ×2 میتوانند حداقل هر لایه از جعبه 3×3×3 را پر کنند؟
پاسخ باز هم منفی است. مساحتی از یک لایه که میتواند توسط یک قطعه پوشانده شود، برابر مساحت یکی از وجههای آن قطعه است. درست است ؟
 وجههای یک قطعه 1×2×2 چگونه هستند ؟
وجههای یک قطعه 1×2×2 چگونه هستند ؟
یک قطعه 1×2×2 دارای دو جفت وجه موازی 1×2 و یک جفت وجه موازی2×2 است.
 مساحت این وجه چقدر است و چه مساحت مشترکی دارند؟
مساحت این وجه چقدر است و چه مساحت مشترکی دارند؟
مساحتها برابر 1×2 = 2 و 2 ×2 = 4 هستند. 2 و 4 هر دو اعداد زوج هستند.
مشاهده میکنیم که یک قطعه 1×2×2 فقط میتواند تعداد زوجی از مکعبها (2 یا 4) را در هر لایه بپوشاند.
 آیا این نکته برای همه قطعههای زوج صادق است؟
آیا این نکته برای همه قطعههای زوج صادق است؟
هر وجه یک قطعه دارای دو طول است. چون قطعههای زوج حداکثر یک طول فرد دارند، هر یک از وجههای آنها حداقل یک طول زوج خواهند داشت. چون زوج × فرد = زوج، مساحت هر وجه زوج خواهد بود. به همین دلیل است که ما آنها را قطعه زوج مینامیم!
ما یاد گرفتیم که مکعبهای با طول یال فرد را نمیتوان فقط با قطعههای زوج ساخت. لایهای با مساحت فرد نیز نمیتواند با قطعههای زوج پر شود. بنابر این، معمای 3×3×3 شماره 2 دارای چند قطعه 1×1×1 است که قطعههای فرد هستند.
در اینجا یک سوال مفید دیگر وجود دارد که باید در نظر بگیرید :
 آیا یکی از دو نوع قطعه (1×1×1 و 1×2×2) «با ارزش» تر از دیگری است ؟
آیا یکی از دو نوع قطعه (1×1×1 و 1×2×2) «با ارزش» تر از دیگری است ؟
بله. اگر ما فقط قطعه 1×1×1 داشته باشیم، هر معمایی ساده و پیش پا افتاده خواهد بود، آیا موافقید ؟ اگر فقط قطعههای 1×2×2 داشته باشیم، همانطور که در بالا نشان داده شد، هیچ جعبه فردی را نمیتوان پر کرد.
سوال واضح این است : در این معما، حداقل تعداد قطعههای 1×1×1 که باید در پر کردن جعبه 3×3×3 استفاد شوند، چقدر است ؟
طبیعتا سوالهای زیر مطرح میشود :
 چرا سه قطعه 1×1×1 کافی است ؟
چرا سه قطعه 1×1×1 کافی است ؟
برای پاسخ به این سوال، تعداد لایههای فرد (لایههایی با مساحت فرد) را با تعداد لایههای با مساحت فرد که میتوان با قطعههای زوج و تنها 3 مکعب پر کرد، مقایسه خواهیم کرد.
 یک جعبه 3×3×3 چند لایه دارد ؟
یک جعبه 3×3×3 چند لایه دارد ؟
در هر یک از سه جهت (طول،عرض، ارتفاع) جعبه دارای 3 لایه است. پس 3 + 3 + 3 = 9 لایه فرد وجود دارد که هنگام پر شدن جعبه پر میشوند.
 چند لایه فرد 3×3 را میتوان با یک قطعه 1×1×1 (و تعدادی قطعه 1×2×2 ) کامل کرد ؟
چند لایه فرد 3×3 را میتوان با یک قطعه 1×1×1 (و تعدادی قطعه 1×2×2 ) کامل کرد ؟
سه لایه : لایه افقی و دو لایه عمودی که حاوی قطعه 1 ×1 ×1 هستند. بنابر این، 3 مکعب میتواند به پر کردن حداکثر 3×3 = 9 لایه کمک کند.
این نشان میدهد که 3 مکعب لازم است و از آنجایی که معما 3×3×2 شماره 2 قابل حل است، 3 مکعب نیز برای پر کردن 9 لایه فرد کافی است.
 در مورد محل قرار گرفتن 3 مکعب در جواب معمای 3×3×3 شماره 2 چه میتوان گفت ؟
در مورد محل قرار گرفتن 3 مکعب در جواب معمای 3×3×3 شماره 2 چه میتوان گفت ؟
در هر یک از 9 لایه فقط میتواند 1 مکعب وجود داشته باشد، نه 0 مکعب و نه 2 مکعب ! در غیر این صورت، 3 مکعب برای پوشاندن 9 لایه کافی نخواهد بود.
این یک پیشرفت برای حل مساله است. علاوه بر این، تنها راه قرار دادن مکعبها در امتداد یک قطراست - یک مکعب در مرکز و دو مکعب دیگر در گوشه های یک قطر. در غیر این صورت، قطعههای بزرگتر 1×2×2 برای پر کردن فضای اطراف 3 مکعب بسیار بزرگ خواهند بود.
بنابر این، یک مکعب را در گوشهای قرار داده و سه قطعه 1×2×2 را به صورت متقارن در اطراف آن مکعب قرار دهید. یک مکعب را در مرکز قرار دهید، یک مکعب دیگر را در گوشه مقابل قرار دهید و ادامه کار ساده است.
 چه چیز دیگری میتوانیم از این راه حل بیاموزیم؟ به عنوان مثال، آیا تقارن دارد ؟
چه چیز دیگری میتوانیم از این راه حل بیاموزیم؟ به عنوان مثال، آیا تقارن دارد ؟
تقارنها پس از قرار دادن مکعب اول در یک گوشه و سه قطعه 1×2×2 در اطراف آن قابل مشاهده هستند. جواب دارای تقارن دورانی120 درجه نسبت به قطر مکعب است (120 درجه = 1/3 دوران یک دایره کامل).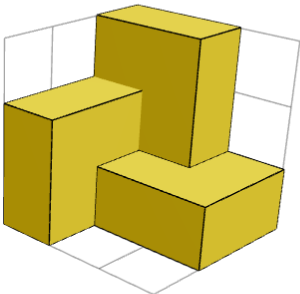
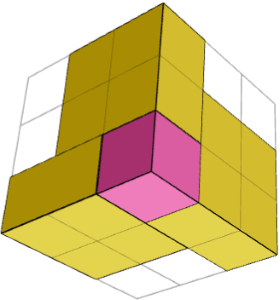
 آیا جواب معما مجموع بلوکهای ساختمانی یکسان یا متقارن است که هر کدام از آنها از چند قطعه تشکیل شده اند ؟
آیا جواب معما مجموع بلوکهای ساختمانی یکسان یا متقارن است که هر کدام از آنها از چند قطعه تشکیل شده اند ؟
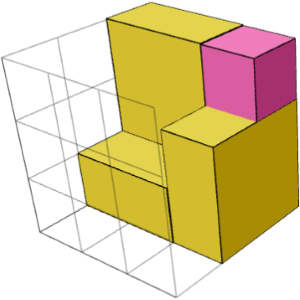
بله. این مکعب مستطیل برابر مجموع 2 بلوک ساختمانی است که متقارن آینهای هستند (1 مکعب در یک گوشه + سه قطعه 1×2×2 در اطراف آن) و یک مکعب در وسط. 2 تصویر بالا یک بلوک ساختمانی را از 2 طرف نشان میدهد.
 آیا راه دیگری برای حل این معما با استفاده از بلوکهای ساختمانی مختلف وجود دارد؟
آیا راه دیگری برای حل این معما با استفاده از بلوکهای ساختمانی مختلف وجود دارد؟
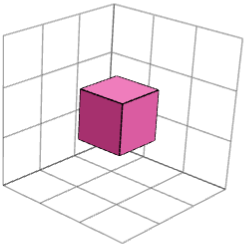
بله. تصاویر زیر، چپ و راست، دو بلوک ساختمانی متقارن آینهای را برای معمای 3×3×3 شماره 2 نشان میدهد. آنها را میتوان با یک مکعب مرکزی (تصویر میانی) ترکیب کرد تا معما را حل کند.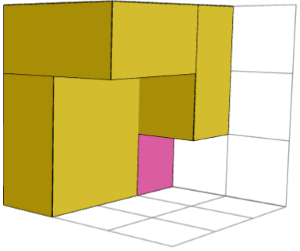
 چرا باید به خود زحمت دهیم و به بلوکهای ساختمانی فکر کنیم ؟
چرا باید به خود زحمت دهیم و به بلوکهای ساختمانی فکر کنیم ؟
استفاده از تعداد کمی از قطعهها و ایجاد بلوکهای ساختمانی متقارن به کمک آنها آسانتر از پر کردن جعبه بزرگتر با تمام قطعهها است.
 آیا میتوان از بلوکهای ساختمانی برای حل معماهای بزرگتر مانند 3×5×7 شماره1 استفاده کرد ؟
آیا میتوان از بلوکهای ساختمانی برای حل معماهای بزرگتر مانند 3×5×7 شماره1 استفاده کرد ؟
بله. جعبههای بزرگتر، حتی اگر طول آنها متفاوت باشد، را میتوان با استفاده از بلوکهای ساختمانی متقارن یکسان/آینهای پر کرد. راههای مختلفی برای حل معما 3×5×7 شماره 1 با استفاده از بلوکهای ساختمانی و یک قطعه فرد مرکزی وجود دارد. حل آن را به شما واگذار میکنیم تا چند نمونه را پیدا کنید.
 چگونه بفهمیم که کدام قطعهها باید یک بلوک ساختمانی را تشکیل دهند ؟
چگونه بفهمیم که کدام قطعهها باید یک بلوک ساختمانی را تشکیل دهند ؟
اجازه دهید ابتدا به مرکز یک مکعب مستطیل فرد فکر کنیم. چون موقعیت مرکز منحصر به فرد است ، اگر میخواهیم یک جواب متقارن داشته باشیم، مرکز باید توسط قطعهای مشابه با شکل جعبه پوشانده شود. مکعب 3×3×3 یک مکعب است، بنابر این، قطعه مرکزی آن باید یک مکعب باشد. یک قطعه 1×2×2 در مرکز تقارن را بر هم میزند.
این بدان معناست که ما 6 قطعه زرد و 1 - 3 = 2 قطعه صورتی برای ساخت تعدادی بلوک ساختمانی یکسان داریم.
 چند بلوک ساختمانی باید سعی کنیم ایجاد کنیم؟
چند بلوک ساختمانی باید سعی کنیم ایجاد کنیم؟
بلوکهای ساختمانی باید مکعب مستطیل منهای قطعه مرکزی را تشکیل دهند. بنابر این، تعداد قطعههای زرد در یک بلوک ساختمانی باید مقسوم علیه 6 (تعداد کل بلوک های زرد) باشد و تعداد قطعههای صورتی یک بلوک ساختمانی باید بر 2 تقسیم شود (تعداد مکعبهای صورتی باقیمانده پس از نگه داشتن یک مکعب برای مرکز).
بنابر این، N یعنی تعداد بلوکهای ساختمانی یکسان برابر بزرگترین مقسوم علیه مشترک تعداد قطعههای یکسان است، در اینجا 6 و 2، که gcd(6,2) = 2 است. بنابر این، ما باید یک بلوک ساختمانی شامل 2/2 = 1 مکعب صورتی و 6/2 = 3 بلوک زرد ایجاد کنیم. این کاری است که ما انجام دادیم.
 الگوریتم ریاضی را خلاصه کنید تا از آن برای معماهای بزرگتر استفاده کنید.
الگوریتم ریاضی را خلاصه کنید تا از آن برای معماهای بزرگتر استفاده کنید.
برای یک جعبه فرد :
- قطعههای فرد را مرتب کنید تا مطمئن شوید که در هیچ لایهای همپوشانی ندارند. آنها باید یک گوشه از جعبه را به گوشه مقابل جعبه وصل کنند. اگر قطعههای فرد مکعب باشند ، قطر را میسازند. اگر قطعههای فرد بزرگتر باشند (1×1×3) ، یک قطر غیر مستقیم تشکیل میدهند.
- اگر فقط یک نوع قطعه زوج وجود دارد، از آنها برای پر کردن جعبه استفاده کنید.
- اگر انواع مختلفی از قطعههای زوج وجود دارد :
- قطعه فرد مرکز را کنار بگذارید. از قطعههای باقیمانده ، بزرگترین مقسوم علیه مشترک تعداد قطعههای انواع مختلف، N، را پیدا کنید. N تعداد بلوکهای ساختمانی است.
- N بلوک ساختمانی یکسان ایجاد کنید و آنها را ، همراه با قطعه مرکزی برای یک جعبه فرد، کنار هم قرار دهید.
در حالی که معماهای کوچک ممکن است به راحتی با آزمون و خطا حل شوند، این استراتژی برای معماهای بزرگتر کار نمیکند. کاوش ما در قطعههای فرد دلیل مهمی را نشان میدهد : قرار دادن قطعههای فرد بسیار مهم است، زیرا راههای بسیار کمی وجود دارد که بتوان آنها را به درستی قرار داد. با استفاده از آزمون و خطا، ممکن است در ابتدای کار اشتباه کرد و پس از قرار دادن قطعههای زیاد متوجه شد که مشکلی پیش آمده است. این امر تعیین علت خطا را بسیار دشوار میکند، بنابر این، هیچ بازخورد قابل استفادهای وجود ندارد. روش آزمون و خطا برای جعبههای بزرگتر موثر نیست. تفکر لازم است.
 بستهبندی تنها با یک نوع قطعه
بستهبندی تنها با یک نوع قطعه
در این بخش، اندازه مکعب مستطیلهایی را که میتوانند از یک نوع قطعه تشکیل شوند بررسی خواهیم کرد. این یک بخش نظری است که برای حل معماهای بالا مورد نیاز نیست. این بخش نیازی به ریاضیات دشوار ندارد.
با تعداد کافی از قطعههای 1×1×1 به راحتی میتوانیم یک مکعب مستطیل با هر اندازهای را بسازیم. اما در مورد قطعههای دیگر، مانند قطعههای 2×3×4 یا 1×2×5 چطور؟ دو سوال اصلی برای بررسی وجود دارد. اول، با توجه به طول یک قطعه و طول یک مکعب مستطیل که داده شده باشند، چگونه میتوانیم تعیین کنیم که آیا مکعب مستطیل را میتوان به کمک کپیهای این قطعه ایجاد کرد یا خیر؟ دوم، چگونه میتوانیم با معلوم بودن یک قطعه، ابعاد یک مکعب مستطیل را که میتواند بسازد را مشخص کنیم ؟ در طول این بخش، هنگام بررسی این دو سوال مهم، سوالهای سادهتری را در نظر خواهیم گرفت.
 آیا میتوان یک مکعب مستطیل 2×6×10 را تنها به کمک قطعههای 1×2×5 ساخت ؟
آیا میتوان یک مکعب مستطیل 2×6×10 را تنها به کمک قطعههای 1×2×5 ساخت ؟
بله ! سه قطعه 1×2 ×5 را میتوان در کنار هم قرار داد تا شکل 1 ×6 ×5 را بسازند (3 & بار 2 = 6). سپس میتوانیم یک شکل 1×6×5 دیگر بسازیم و با کنار هم گذاشتن آنها یک شکل بزرگتر 1×6×10 بسازیم. در نهایت، دو شکل 1×6×10 را میتوان در کنار هم قرار داد تا یک مکعب مستطیل 2×6×10 را تشکیل دهند.
 آیا میتوان یک مکعب مستطیل 10×12×14 را تنها با استفاده از قطعههای با اندازه 2×5×6 ساخت ؟
آیا میتوان یک مکعب مستطیل 10×12×14 را تنها با استفاده از قطعههای با اندازه 2×5×6 ساخت ؟
 نکته
نکته
لازم نیست که تصور کنیم ، قطعهها چگونه باید چیده شوند.
 نکته دیگر ؟
نکته دیگر ؟
یک قطعه 2 ×5 ×6 همان قطعه 5 ×6×2 است زیرا میتوان آن را چرخاند.
 پاسخ
پاسخ
بله. چون 10÷5 = 2، 12÷6 = 2 و 14÷2 = 7، مکعب مستطیل بزرگتر را میتوان به عنوان آرایش 2×2×7 از قطعههای 5×6×2 در نظر گرفت. تمام قطعههای 5×6×2 را میتوان در یک جهت قرار داد.
 چگونه میتوانیم این یافتهها را تعمیم دهیم؟
چگونه میتوانیم این یافتهها را تعمیم دهیم؟
فرض کنید ما فقط قطعههایی با اندازه x × y × z داریم. در این صورت، ساختن مکعب مستطیل X ×Y × Z امکانپذیر است اگر عددهای صحیح و مثبت A، B، C وجود داشته باشند بطوریکه Ax، By و Cz به ترتیب، برابر X، Y و Z باشند.
 در این مورد از چند قطعه استفاده خواهد شد؟
در این مورد از چند قطعه استفاده خواهد شد؟
ما میتوانیم A قطعه را در یک جهت، B قطعه را در جهت دیگر و C قطعه را در جهت سوم بچینیم. در مجموع، از A× B × C قطعه استفاده خواهد شد.
 چرا Ax، By و Cz به هر ترتیبی میتوانند برابر با X، Y و Z باشند؟
چرا Ax، By و Cz به هر ترتیبی میتوانند برابر با X، Y و Z باشند؟
یک جعبه با اندازه X & ضربدر Y & برابر Z همان مکعب Z & x & Y است. ترتیب طول ها مهم نیست زیرا مکعب را میتوان چرخاند.
 آیا این درست است که هر مکعب مستطیلی که از قطعههای 1×2×3 تشکیل شده است باید دارای طولهای A ، B × 2، C × 3 به ازای عددهای صحیح مثبت و مناسبی مانند A، B، C باشد ؟
آیا این درست است که هر مکعب مستطیلی که از قطعههای 1×2×3 تشکیل شده است باید دارای طولهای A ، B × 2، C × 3 به ازای عددهای صحیح مثبت و مناسبی مانند A، B، C باشد ؟
خیر. اگر همه قطعههای 1×2×3 در یک جهت چیده شوند، مکعب مستطیل دارای اندازه A × (B × 2) × (C ×3) خواهد بود. اما قطعهها میتوانند جهتهای متفاوتی داشته باشند و باز هم یک مکعب مستطیل را تشکیل دهند. به عنوان مثال، قطعههای 1×2×3 میتوانند یک مکعب 1×5×6 را تشکیل دهند، با اینکه 1، 5 و 6 هیچ تناسبی با A، B × 2 و C × 3 ندارند. مثال دیگر، معمای1×7×10 شماره1 است که از قطعههای 1×2×5 تشکیل شده است.
 در این دو مثال، چه رابطهای بین طولهای قطعه و طولهای مکعب مستطیل وجود دارد ؟
در این دو مثال، چه رابطهای بین طولهای قطعه و طولهای مکعب مستطیل وجود دارد ؟
در هر دو مثال، یکی از طولهای مکعب مستطیلها مجموع دو تا از طولهای قطعه است. طول دیگر مکعب مستطیل lcm (کوچکترین مضرب مشترک) همان دو طول قطعه است. در مورد مکعب مستطیل 1×5×6 که از قطعههای 1×2×3 تشکیل شده است، داریم 1×5×6 = 1 × (2 + 3) × lcm(2,3). به طور مشابه، 1×7×10 = 1 × (2 + 5) ×lcm(2,5).
 چگونه میتوانیم از این واقعیت برای یافتن راهی برای تولید طول مکعبهایی که میتوانند از یک قطعه معین ساخته شوند، استفاده کنیم ؟
چگونه میتوانیم از این واقعیت برای یافتن راهی برای تولید طول مکعبهایی که میتوانند از یک قطعه معین ساخته شوند، استفاده کنیم ؟
ما با نشان دادن طول یک قطعه به صورت سهتایی مرتب شروع میکنیم. به عنوان مثال، یک قطعه 1×2×3 با (1, 2, 3) نشان داده میشود. اکنون، 3 عمل وجود دارد که میتوانیم بارها و بارها انجام دهیم تا طول مکعب مستطیلهایی را که میتوانند از این قطعه تشکیل شوند، به دست آوریم. آنها عبارتند از :
- ترتیب طول ها را تغییر دهید. این عمل با نام جایگشت شناخته میشود. در اینجا، این عمل نشان دهنده دوران در فضای سه بعدی است. به عنوان مثال
(1، 2، 3) → (2، 3، 1). - طولها را به ترتیب در اعداد صحیح و مثبت A، B و C ضرب کنید. این عمل مربوط به ساختن یک مکعب مستطیل بزرگتر با قرار دادن A قطعه در یک جهت ، B قطعه در جهت دیگر و C قطعه در جهت سوم است. به عنوان مثال، میتوانیم 1×2×3 را در 1، 4 و 3 ضرب کنیم و به مکعب مستطیل (1، 2، 3) → (1 × 1، 4 × 2، 3 × 3) = (1، 8، 9) را به دست آوریم.
- دو طول را بردارید و یکی را با مجموع آنها و دیگری را با lcm آن دو عدد جایگزین کنید. این عمل، مربوط به تشکیل یک مکعب مستطیل بزرگتر با قطعههایی است که در جهتهای مختلف چیده شده باشند. به عنوان مثال ، با انتخاب طول های 2 و 3 خواهیم داشت : (1 ، 2 ، 3) → (1 ، 2 + 3 ، LCM (2،3)) = (1 ، 5 ، 6)
 آیا میتوان قطعهها را به یک روش چهارم کنار هم چید تا اینکه یک مکعب مستطیل ساخته شود که شکل آن با نتیجه عمل سوم متفاوت باشد ؟
آیا میتوان قطعهها را به یک روش چهارم کنار هم چید تا اینکه یک مکعب مستطیل ساخته شود که شکل آن با نتیجه عمل سوم متفاوت باشد ؟
بله. قطعهای با اندازههای x ×y × z را در نظر بگیرید. عمل سوم یک مکعب مستطیل با اندازه x × (y + z) × lcm(y,z) تولید میکند که در آن، یک طول x از قطعه در طولهای مکعب مستطیل باقی میماند.
یک روش مشابه اما متفاوت این است که باز همlcm(y,z)/y قطعه را در کنار یکدیگر قرار دهیم و lcm(y,z)/y قطعه را هم در کنار یکدیگر مانند قبل, و سپس یکی از این دو دسته را به اندازه 90 درجه بچرخانیم بطوریکه دو بلوک دارای طول یکسان lcm(y,z), و ارتفاع های متفاوت باشند. به بیان ریاضی، x× y × lcm(y,z) و x × z× (y,z) را برای ساختن x × (y + z)× (y,z) کنار هم نمیگذاریم. در عوض، یکی از آنها، مثلا x × z × (y,z) به صورت z ×x × (y,z) چرخانده میشود و سپس به هم متصل میشوند.
مساحت قاعده مستطیلی برابر (y + z) × lcm(y,z) نیست، بلکه (x + z) × lcm(y,z) است. آنگاه دو بلوک ساختمانی x × y × lcm(y,z) و z × x ×lcm(y,z) به ترتیب، دارای طول x و z در جهت X هستند.
کنار هم گذاشتن تعداد lcm(x,z)/x بلوک ساختمانی با ارتفاع x و تعداد lcm(x,z)/z بلوک ساختمانی با ارتفاع z، هر دو دسته به ارتفاع lcm (x,z) میرسند. هنگامی که آنها به هم متصل میشوند، نتیجه کار یک مکعب مستطیل با اندازه lcm(x,z) ×(x + z) × lcm(y,z) است که شکل و اندازههای متفاوتی نسبت به هر مکعب حاصل از عمل سوم دارد.
میتوان این عمل را به هر ترتیبی تکرار کرد، ابتدا یک مکعب مستطیل از یک قطعه تولید کرد و سپس از این مکعب مستطیل به عنوان یک «قطعه» برای تولید یک مکعب مستطیل بزرگتر استفاده کرد. ما قبلا بحث کردیم که چگونه یک مکعب مستطیل 2×6×10 را میتوان از قطعههای 1×2×5 تشکیل داد. در این حالت، فقط یک عمل مورد نیاز است، به ترتیب، ضرب در 2، 3 و 2 : (1، 2، 5) → (2 × 1، 3 × 2، 2 × 5) = (2، 5، 10).
بنابر این، قطعههایی با اندازه x × y × z نه تنها میتوانند مکعبهایی با اندازه Ax × By × Cz بسازند، بلکه به عنوان مثال، با اندازه x × (y + z) × lcm(y,z) نیز میتوانند بسازند، که در آن lcm(y,z) کمترین مضرب مشترک y و z است. قرار دادن چندین مورد از این بلوکهای سازنده در کنار هم، مکعبهایی با اندازه Ax × B(y + z) + C(lcm(y,z)) میسازد.
اکنون نوع خاصی از قطعه را در نظر خواهیم گرفت. یک قطعه هارمونیک است اگر هر یک از طول های بزرگتر آن بر طول کوچکتر بعدی قابل تقسیم باشد. به عنوان مثال، یک قطعه 1×2×6 هارمونیک است زیرا 2÷1 =2 و 6÷2 = 3. قطعه 1×4×6 هارمونیک نیست زیرا 6 مضربی از 4 نیست.
 آیا قطعه 1×2×3 هارمونیک است ؟
آیا قطعه 1×2×3 هارمونیک است ؟
خیر، زیرا 3 بر 2 بخشپذیر نیست.
 قطعههای هارمونیک چه ویژگی خاصی در بستهبندی خاص دارند ؟ آنها چگونه با بحث ما در مورد طول قطعهها و مکعب مستطیلها ارتباط دارند ؟
قطعههای هارمونیک چه ویژگی خاصی در بستهبندی خاص دارند ؟ آنها چگونه با بحث ما در مورد طول قطعهها و مکعب مستطیلها ارتباط دارند ؟
قبلا مشاهده کردیم که هر قطعه میتواند یک مکعب مستطیل تشکیل دهد که طول آن چند برابر طول قطعه باشد. به نظر میرسد که طول هر مکعب مستطیل که توسط قطعههای هارمونیک یکسان تشکیل شده است باید چند برابر طول قطعهها باشد. یعنی اگر یک قطعه هارمونیک دارای طولهای x ، y و z باشد ، هر مکعب مستطیل تشکیل شده از کپیهای این قطعه باید یک طول قابل تقسیم بر x ، دیگری بر y و سومی قابل تقسیم بر z داشته باشد. در حالی که این ویژگی یک گزاره ساده به نظر میآید، اما اثبات آن به مفاهیمی فراتر از محدوده این وب سایت نیاز دارد. پیوند مربوط به اثبات آن را میتوانید در بخش «قدردانی» بیابید.
 چگونه این ویژگی با چهار عملی که در بالا مورد بحث قرار دادیم سازگار است ؟
چگونه این ویژگی با چهار عملی که در بالا مورد بحث قرار دادیم سازگار است ؟
ما میتوانیم یک قطعه را به عنوان یک مکعب مستطیل که از یک کپی از آن قطعه تشکیل شده است تصور کنیم. یک قطعه x × y ×z یک مکعب مستطیل x × y ×z نیز هست. طولهای این مکعب مستطیل مضربی از طولهای قطعه است ، زیرا هر عدد مضربی از خودش است. نشان خواهیم داد که چرا چهار روشی که معرفی کردیم مکعب مستطیلهایی تولید میکنند که طولهای آنها هم چند برابر طولهای قطعه است.
- تغییر ترتیب طولها (جایگشت) : این یک دوران است و در واقع طولهای مکعب مستطیل را تغییرنمیدهد. طولهای مکعب مستطیل همچنان چند برابر طولهای قطعه خواهد بود.
- ضرب طولهای مکعب مستطیل در عددهای صحیح مثبت : اگر طولهای مکعب مستطیل از قبل، مضرب طولهای قطعه باشد ، این وضعیت تغییر نخواهد کرد و آنها به سادگی به مضربهای بزرگتری تبدیل میشوند. اگر X = Ax مضربی از x باشد ، DX = DAx نیز مضربی از x است، برای هر عدد صحیح مثبت D.
- جایگزینی دو طول با مجموع آنها و LCM: به همین دلیل است که قطعههای هارمونیک مهم هستند. ما باید از تعریف قطعههای هارمونیک استفاده کنیم. فرض کنید ما با یک قطعه هارمونیک (x ، y ، z) شروع کردهایم که قبلا مکعب مستطیل را از آن تشکیل داده ایم (Ax ، By ، Cz). ترتیب طولها مهم نیست زیرا مکعب مستطیل را میتوان چرخاند. اکنون عملیات سوم را روی هر دو طول مکعب انجام خواهیم داد، مثلا Ax و By: (Ax، By، Cz) → (Ax + By، LCM(Ax,By)، Cz). حال، چون قطعه (x، y، z) هارمونیک است، یکی از دو طول x و y مضربی از دیگری است. فرض کنید y مضربی از x است. بنابر این، By نیز مضربی از x است و چون Ax نیز هست، مجموع Ax + By مضربی از x است. در مرحله بعد، lcm(Ax,By) کوچکترین مضرب مشترک Ax و By است، بنابر این، طبق تعریف، مضربی از By است، پس بر y بخشپذیر است. در نهایت، Cz مضربی از z است. بنابر این، طول مکعب مستطیل جدید (Ax + By، LCM(Ax,By)، Cz) هنوز هم چند برابر طول قطعه است.
- در مورد عمل چهارم چطور؟ چون که این عملیات شبیه عملیات سوم است، استدلال ارائه شده در بالا را میتوان برای این مورد تطبیق داد. ما آن را به عنوان یک تمرین میگذاریم.
ما نشان دادهایم که چهار عملیات، که به طور مکرر و به هر ترتیبی بر روی هر قطعه هارمونیک انجام میشود، منجر به یک مکعب مستطیل میشود که طولهای آن چند برابر طولهای قطعه است. توجه به این نکته مهم است که هنگام بحث در مورد عملیات سوم (و چهارم !) ، به این واقعیت تکیه میکنیم که قطعه هارمونیک است. وقتی که یک قطعه هارمونیک نباشد، این استدلال درست نیست. این تفاوت اصلی بین قطعههای هارمونیک و غیر هارمونیک است. برای قطعههای هارمونیک، روشهای سوم و چهارم در مقایسه با دو روش اول شکلهای بیشتر ایجاد نمیکنند.
در نتیجه، هر مکعب مستطیل تشکیل شده از قطعههای هارمونیک میتواند همه قطعهها را در یک جهت داشته باشد. بنابر این، اگر میخواهیم از قطعههای هارمونیک مشابه، یک مکعب مستطیل تشکیل دهیم ، کافی است سعی کنیم همه آنها را در یک جهت مرتب کنیم. اگر این کار امکانپذیر نباشد، مکعب مستطیل نمیتواند ساخته شود.
چون یک قطعه 1×2×2 هارمونیک است، هر مکعب مستطیلی که از کپیهای این قطعه تشکیل شده است باید دارای طولهای A، B ×2 و C × 2 ، به ازای عددهای صحیح مناسب A، B و C باشد. تصویر زیر یک مکعب مستطیل 5×4×4 را نشان میدهد که توسط قطعههای 1×2×2 ساخته شده است که همگی جهت یکسانی دارند.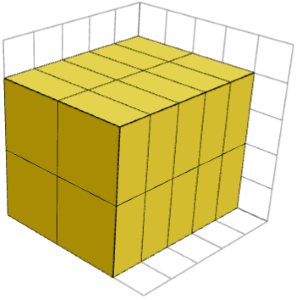
 مقادیر A، B و C چیست؟
مقادیر A، B و C چیست؟
با فرض اینکه A، B ×2 و C × 2 به ترتیب، برابر با 5، 4 و 4 باشند، آنگاه خواهیم داشت A = 5 /1 = 1، B = 4/2 = 2 و C = 4/2 = 2.
 هنگام بستهبندی با قطعههای هارمونیک، آیا قطعهها باید در یک جهت قرار گیرند؟
هنگام بستهبندی با قطعههای هارمونیک، آیا قطعهها باید در یک جهت قرار گیرند؟
نه ! اگرچه همواره ممکن است که همه قطعهها جهت یکسانی داشته باشند ، اما ممکن است چیدمانهای دیگری نیز وجود داشته باشد ، اما آنها شکلهای جدیدی را تشکیل نمیدهند. تصویر زیر روش متفاوتی را برای ساختن مکعب مستطیل 5×4×4 به کمک قطعههای 1×2×2 را نشان میدهد.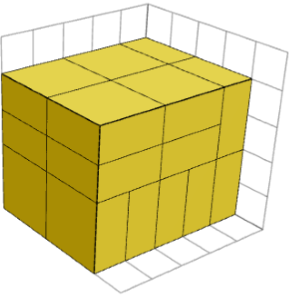
 قوانین قطعههای غیر هارمونیک چیست؟
قوانین قطعههای غیر هارمونیک چیست؟
هنگام کار با یک قطعه غیر هارمونیک x × y × z، مکعب مستطیلهایی وجود دارند که میتوانند ساخته شوند که اندازه آنها به ازای هیچ عدد صحیح A، B، C ، به صورت Ax × By × Cz نباشد. به عنوان مثال، یک مکعب مستطیل1×5×6 را میتوان با قطعههای 1×2×3 ایجاد کرد. این نتیجه عملیات سوم است، همانطور که قبلا بحث شد.
توجه به این نکته ضروری است که تعداد مکعبها در مکعب مستطیل همیشه باید بر تعداد مکعبهای قطعه بخشپذیر باشد. هنگامی که طولهای مکعب هیچکدام مضربی از طولهای متفاوت قطعه نباشد، یکی از طولهای مکعب مستطیلها به دلیل روشهای سوم و چهارم، یک مضرب مشترک با حداقل 2 طول قطعه خواهد بود. از این واقعیت میتوان برای تعیین اینکه آیا مکعب مستطیلهای خاصی میتوانند از قطعههای غیر هارمونیک تشکیل شوند یا خیر استفاده کرد.
 چند سوال برای مرور آنچه بررسی کرده ایم:
چند سوال برای مرور آنچه بررسی کرده ایم:
 آیا قطعه 2 ×4 ×12 میتواند یک مکعب مستطیل با اندازه 4 ×8 ×36 را تشکیل دهد؟ در مورد مکعب با اندازه 10 ×10 ×12 چطور؟
آیا قطعه 2 ×4 ×12 میتواند یک مکعب مستطیل با اندازه 4 ×8 ×36 را تشکیل دهد؟ در مورد مکعب با اندازه 10 ×10 ×12 چطور؟
چون 4÷2 = 2، 8÷4 = 2 و 36÷12 = 3، میتوان مکعب مستطیل 4×8×36 را ساخت.
یکی از طولهای مکعب مستطیل 10×10×12 بر 12 بخشپذیر است. طولهای دیگر 10 و 10 هستند که هیچ یک از آنها بر 4 بخشپذیر نیستند. بنابر این، طولهای مکعب مستطیل 10×10×12 مضربی از طول قطعه نیست. چون 12÷4 = 3 و 4÷2 = 2، قطعه هارمونیک است، پس یک مکعب مستطیل 10×10×12 را نمیتوان با قطعههای با اندازه 2×4×12 ساخت.
 آیا قطعههای اندازه 1 × 3 ×5 میتوانند یک مکعب مستطیل با اندازه 2 ×15 ×8 تشکیل دهند؟ در مورد مکعب 3×9×14 چطور؟
آیا قطعههای اندازه 1 × 3 ×5 میتوانند یک مکعب مستطیل با اندازه 2 ×15 ×8 تشکیل دهند؟ در مورد مکعب 3×9×14 چطور؟
چون 5 بر 3 بخشپذیر نیست، قطعه هارمونیک نیست. نمیتوانیم از اطاعات خود در مورد قطعههای هارمونیک استفاده کنیم.
میتوان با این قطعهها یک مکعب 2×15×8 تشکیل داد. سه قطعه 1 ×3 ×5 میتوانند شکل 1 ×3 ×15 (یا 1 ×15 ×3) را تشکیل دهند و 5 قطعه که به طور متفاوتی چیده شدهاند میتوانند شکل 1 ×15 ×5 را تشکیل دهند. از این دو شکل میتوان برای ایجاد یک مکعب 1×15×8 استفاده کرد که دو تا از آنها میتوانند یک مکعب مستطیل 2×15×8 را تشکیل دهند. اکنون میتوانیم از عملهایی که در مورد آنها صحبت کردیم استفاده کرده و بنویسیم : (1، 3، 5) → (1، 3 + 5، lcm(3،5)) = (1، 8، 15) → (2، 8، 15) → (2، 15، 8).
اگر قطعههای 1×3×5 با هم ترکیب شوند، تعداد کل مکعبها مضربی از 5 است. چون 3 ×9 × 14 بر 5 بخش پذیر نیست، یک مکعب 3×9×14 را نمیتوان از قطعههای با اندازه 1×3×5 ایجاد کرد.
 خلاصهای از قوانین قطعههای هارمونیک و غیر هارمونیک
خلاصهای از قوانین قطعههای هارمونیک و غیر هارمونیک
در اینجا مروری بر آنچه آموختهایم آورده شده است :
- اگر طول مکعب مضربی از طول یک قطعه باشد، میتوان آن را از کپیهای آن قطعه تشکیل داد، صرف نظر از اینکه قطعه هارمونیک است یا خیر. چنین مکعبهایی را میتوان با همه قطعهها در جهت یکسان تشکیل داد ، اما ممکن است ترتیباتی نیز وجود داشته باشد که در آن قطعهها جهت گیریهای متفاوتی داشته باشند.
- اگر یک قطعه هارمونیک باشد، هر مکعب تشکیل شده باید دارای طولهایی باشد که چند برابر طول قطعه باشد. در نتیجه، هر مکعبی که از قطعههای هارمونیک تشکیل شده است ممکن است همه قطعهها را در جهت یکسان داشته باشد، اگرچه این مورد همیشه ضروری نیست.
- اگر یک قطعه هارمونیک نباشد ، میتوان مکعبهایی را تشکیل داد که طول آنها مضربی از طول قطعه نیست (به عملیات سوم و چهارم مراجعه کنید). در این حالت ، همه قطعهها نمیتوانند جهت یکسانی داشته باشند. با استفاده از قطعههای غیر هارمونیک، میتوان با استفاده از 4 روشی که قبلا توضیح داده شد، مکعبهایی با اشکال مختلف ایجاد کرد.
 آیا این مشاهدات فقط در سه بعد معتبر هستند ؟
آیا این مشاهدات فقط در سه بعد معتبر هستند ؟
خیر. در این زمینه، هیچ چیز خاصی در مورد 3 بعد وجود ندارد. در واقع قرار دادن یکی از طولها برابر با 1 معادل کاهش مساله به 2 بعد است. نتایج در بیش از 3 بعد نیز معتبر است. به عنوان مثال، یک قطعه 1×3×12×24 هارمونیک است. بنابر این، هر مکعب 4 بعدی که از این قطعههای 4 بعدی تشکیل شده است باید دارای ابعاد A، B ×3، C × 12 و D × 24 به ازای اعداد صحیح مثبت و مناسب A، B، C و D باشد.
 چگونه میتوانیم معماهای بستهبندی دستساز داشته باشیم ؟
چگونه میتوانیم معماهای بستهبندی دستساز داشته باشیم ؟
ما نمیتوانیم به شما بگوییم که چگونه قطعههای 4 بعدی را بسازید :) اما در حالت 3 بعدی، اگر شما تعداد زیادی تاس دارید، میتوانید آنها را به هم بچسبانید تا قطعههای مختلفی ساخته شوند.
به جای جعبه 5×5×5 میتوان از جعبه کفش استفاده کرد. اگر کسی آن را به صورت اریب نگه دارد، قطعهها در جایی که قرار گرفتهاند باقی میمانند.
برخی از معماها دارای ارتفاع 1 هستند (به عنوان مثال، 1×7×10 شماره1) و بنابر این، معماهای دو بعدی هستند. میتوان مستطیلها را از کاغذ نقاشی برش داد و از آنها به عنوان قطعههای این معماها استفاده کرد.
 قدردانی
قدردانی
علاقه ما به معمای بستهبندی با دیدن نسخه چوبی معمای5x5x5 شماره1 در یک نمایشگاه ریاضی شعلهور شد. پس از مراجعه به نویسنده آن، ریاضیدان مشهور جان هورتون کانوی، معماهای x3x3 شماره2، 5x5x5 شماره2 و 5x5x5 شماره3 متعلق به او را هم پیدا کردیم.
بخش «بستهبندی تنها با یک نوع قطعه» از کار ریاضیدان هلندی دو برویین (de Bruijn) الهام گرفته شده است. برای کسب اطلاعات بیشتر در مورد مشاهدات دو برویین در مورد بستهبندی قطعههای مستطیلی، به این مقاله مراجعه کنید. میتوانید اثبات دو بروین در مورد خواص قطعههای هارمونیک را اینجا بخوانید.





برای به روز رسانی عضو شوید و یا ما را دنبال کنید: