Упаковка©
Эта головоломка выиграна/сыграна: 16279/24796
Почему я должен прочитать эту «Пищу для размышлений»?
Потому что вы будете удивлены.
Попробовав несколько упаковываемых головоломок, какую область математики вы считаете наиболее полезной для их решения:
1) Алгебра, 2) Теория вероятностей, 3) Геометрия, 4) Теория чисел, 5) Симметрии, 6) Другая область?
Наиболее полезным оказывается подумать о делимости чисел, особенно о делимости на 2. Это предмет теории чисел. Вещи, которые мы складываем, являются геометрическими объектами, но это не значит, что для решения головоломок нужны геометрические знания. Из геометрии нам нужно знать, какова площадь квадрата или прямоугольника, но не более того.
Для некоторых головоломок также очень полезны размышления о симметрии.
Быстрые подсказки
Это подсказки для тех, кто ищет помощи, но не интересуется математическими предпосылками.
- Глядя на числа рядом с надписью «Эта головоломка выиграна/разыграна» для каждой головоломки, проверьте, какие из них самые простые. Начинать с самых простых головоломок всегда хорошая идея, и это даст вам практику в обращении с интерфейсом.
- Головоломки "2×3×3 1" и "2×3×3 2" легко решаются методом проб и ошибок.
- Если ваша первая попытка на головоломке "1× 7× 10 1" не увенчалась успехом, поверните части при следующей попытке.
- "1×7×7 1" - это головоломка, в которой помогает размышление о симметрии. Причина в том, что контейнер (сетка) имеет квадратное основание с 4 одинаково длинными сторонами, а у нас есть 4 длинных куска одинаковой формы. Поэтому их следует располагать симметрично. Есть только одна фиолетовая фигура квадратной формы. Чтобы получить симметричное на 90° вращательное решение, эта деталь должна находиться посередине. Любое другое место нарушило бы 90°-симметрию раствора.
- Головоломки с более темными кнопками требуют больше размышлений. Начните с полного понимания головоломки "3× 3×3 2", прежде чем переходить к головоломкам 5×5×5.
Как можно решить эти головоломки без проб и ошибок?
Вот несколько советов:
- Разделите сложную задачу на более легкие, т.е. на подцели. Например, чтобы заполнить всю емкость, нужно заполнить каждый слой.
- Расположите детали симметричным образом, особенно если контейнер симметричен, как куб 3× 3× 3 или контейнер квадратной формы 1× 7× 7.
- Извлекайте максимум пользы из предоставленной информации. Каковы размеры деталей? Сколько из них имеют одинаковую форму?
Оставшаяся часть этой «Пищи для размышлений» имеет цель решить все головоломки без проб и ошибок, вместо этого придумывая простые вопросы и отвечая на них.
Определения
Для ясности, вот несколько терминов, которые мы будем использовать для обсуждения проблем с упаковкой:
Кусок
Одна из фигур, которые будут складываться в более крупное твердое тело.
Нечетная фигура — это фигура, длина которой нечетна, например, 1× 1× 1 или 1× 3× 5 piece.
Фигура считается четной, если она имеет по крайней мере две четные длины, например, 1×2×4 или 2×2×2.
Все ли фигуры четные или нечетные?
НЕТ. Фигура с ровно одной четной длиной, например 1&умно2&умножить на 3, не подходит ни под одно из определений. В следующих разделах мы сосредоточимся на четных и нечетных фигурах.
Кубоид/Контейнер
Кубоид представляет собой прямоугольную призму. Мы используем слово «контейнер» для обозначения пустой оболочки кубоида. Мы называем «кубоидным» содержимое контейнера. Емкость заполняется кусочками, а из кусочков создается кубоид.
Слой
Слой – это срез толщиной 1 в направлении, параллельном лицевой стороне контейнера. Контейнер 3× 4× 5 имеет 3 слоя размером 4× 5, 4 слоя размером 3× 5 и 5 слоев размером 3× 4.
Сколько слоев у контейнера 1× 5×7?
Он имеет один слой 5× 7, пять слоев 1× 7 и семь слоев 1× 5. В сумме он имеет 1 + 5 + 7 = 13 слоев.
Куб
В частности, куб 1× 1× 1, а не больший куб. Фишка 1× 1× 1 состоит из 1 кубика, а фигура 1× 1× 3 состоит из 1 × 1 × 3 = 3 кубика.
Стандартный блок
Несколько частей, прикрепленных друг к другу, образуют строительный блок. Интересные строительные блоки будут иметь симметрию. Для сложных головоломок контейнер заполнят несколько идентичных или идентичных зеркально идентичных строительных блоков плюс центральный элемент.
Стратегия
Половина решения трудной проблемы заключается в том, чтобы разбить трудную проблему на более мелкие проблемы.
Для этого следует задать себе простые вопросы. Следующие вопросы будут полезны при решении паковых головоломок.
Можно ли образовать каждый кубоид из кусочков размером 1&умножение2&умножение2 раза2? Например, можно ли сформировать кубоид 3×3×3, используя только кусочки размера 1×2×2 ?
НЕТ. Фишка 1&умножение2&умножение2 на 2 состоит из четного количества кубиков. Следовательно, любое количество 1&умножение2&умножение2 штук вместе будет иметь четное общее количество кубиков. Поскольку кубоид 3&умножение3&умножить 3 состоит из нечетного числа кубиков, он не может быть сформирован таким образом.
В следующих нескольких разделах мы рассмотрим, как делимость, особенно на 2, определяет, как должны быть размещены элементы для решения определенных головоломок.
Может ли 1×2×2 штуки хотя бы заполнить какой-либо слой контейнера 3×3×3?
Ответ снова НЕТ. Область в слое, которая может быть занята произведением, — это площадь одной из граней изделия, верно?
Какие лица у фигуры 1&умножение2&умножение2?
Фигура 1× 2× 2 имеет две пары параллельных граней 1× 2 и одну пару граней 2× 2.
Каковы области этих лиц, и что у них общего?
Площади равны 1 × 2 = 2 и 2 × 2 = 4. 2 и 4 являются четными числами.
Мы видим, что фишка 1× 2× 2 может занимать только четное количество кубиков (2 или 4) в каждом слое.
Справедливо ли это для всех четных изделий?
Каждая сторона изделия имеет две длины. Поскольку четные фигуры имеют не более одной нечетной длины, то каждая из их граней будет иметь по крайней мере одну четную длину. Поскольку четное × нечетное = четное, площадь каждой грани будет четной. Вот почему мы называем их ровными частями!
Мы узнали, что кубоиды с нечетными длинами сторон не могут быть сформированы только из четных частей. Слой с нечетной областью также не может быть заполнен четными частями. Таким образом, пазл "3×3×3 2" имеет несколько 1×1×1 частей, которые являются нечетными частями.
Вот еще один полезный вопрос, над которым стоит задуматься:
Является ли один из двух типов фигур (1×1×1 и 1×2×2) более «ценным», чем другой?
ДА. Если бы у нас было только 1&умножение1&умножение1 кусочков, то любая головоломка была бы тривиальной, согласитесь? Если бы у нас было только 1&раз2&умножение2 штуки, то нечетная емкость не могла бы быть заполнена, как показано выше.
Очевидный вопрос: каково минимальное количество 1×1×1 штук, которое может заполнить контейнер 3×3×3?
Естественно, возникают следующие вопросы:
Почему достаточно трех 1&умно1&умно1 штук?
Чтобы ответить на этот вопрос, мы сравним количество нечетных слоев (слоев с нечетной площадью) с количеством слоев с нечетной площадью, которые могут быть заполнены четными частями и всего 3 кубиками.
Сколько слоев в контейнере 3× 3×3?
В каждом из трех направлений (ширина, высота, глубина) контейнер имеет 3 слоя. Есть 3 + 3 + 3 = 9 нечетных слоев, которые заполняются при заполнении контейнера.
Сколько нечетных слоев 3× 3 можно заполнить одной штукой 1×1×1 (а некоторые даже 1×2×2 штуки)?
Три слоя: горизонтальный слой и два вертикальных слоя, которые содержат 1&умно1 и умножить на 1 кусок. Следовательно, 3 кубика могут помочь заполнить максимум 3 &умножить на 3 = 9 слоев.
Это показывает, что необходимо 3 кубика, и поскольку головоломка «3× 3× 2» решаема, 3 кубиков также достаточно, чтобы заполнить 9 с лишним слоев.
Что это говорит нам о расположении 3 кубов в
Головоломка "3×3×3 2"?
В каждом из 9 слоев может быть только 1 кубик, не 0 кубиков и не 2 кубика! В противном случае 3 кубиков будет недостаточно для 9 слоев.
Это прорыв в решении проблемы. Кроме того, единственный способ разместить кубики - по диагонали - один куб в центре, а два других куба - в противоположных по диагонали углах. В противном случае громоздкие кусочки 1× 2× 2 будут слишком большими, чтобы заполнить пространство вокруг 3 кубиков.
Поэтому положите один кубик в угол, а вокруг этого куба симметрично три фигуры 1× 2×2. Поставьте один кубик в центр, один в противоположный угол, а остальное будет очевидно.
Что еще мы можем извлечь из этого решения? Например, есть ли у него симметрии?
Симметрии становятся видимыми после того, как первый кубик будет помещен в угол и три фигуры 1× 2× 2 вокруг него. Решение имеет вращательную симметрию на 120° с диагональю куба в качестве оси вращения (120° = 1/3 полного круга вращения).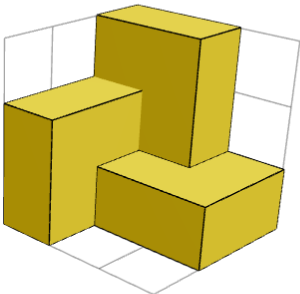
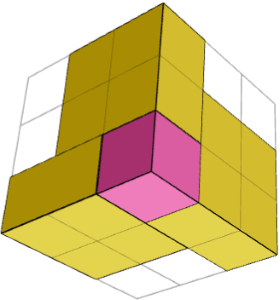
Является ли решение суммой одинаковых или симметричных строительных блоков, каждый из которых состоит из нескольких частей?
ДА. Кубоид — это сумма 2 зеркально симметричных строительных блоков (1 куб в углу + три 1&умножение 2&умножение на 2 штуки вокруг него) и одного куба посередине. На предыдущих 2 изображениях показан один строительный блок с 2 сторон.
Есть ли другой способ решить эту головоломку, используя различные строительные блоки?
ДА. На левом и правом изображениях ниже показаны два зеркально-симметричных строительных блока для головоломки "3× 3× 3 2". Их можно объединить с центральным кубом (средним изображением) для решения головоломки.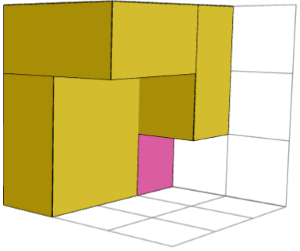
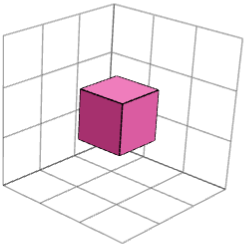
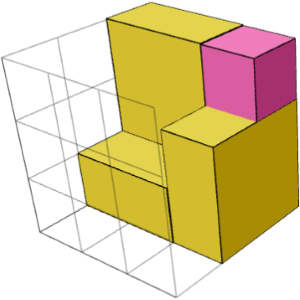
Почему мы должны думать о строительных блоках?
Проще использовать небольшое заданное количество штук и создать из них что-то симметричное, чем заполнять всеми кусочками большую емкость.
Можно ли использовать строительные блоки для решения больших головоломок, таких как "3× 5× 7 1" ?
ДА. Большие контейнеры, даже если их длина разная, могут быть заполнены с использованием идентичных/зеркально симметричных строительных блоков. Существует несколько способов решения головоломки «3×5×7 1» с использованием строительных блоков и нечетной центральной фигуры. Мы оставляем вам возможность найти несколько примеров.
Как узнать, какие части должны составлять строительный блок?
Давайте сначала подумаем о центре нечетного кубоида. Поскольку центральное положение уникально, если мы хотим получить симметричное решение, центр должен быть занят деталью той же формы, что и контейнер. Кубоид 3&умножение3&умножение на 3 является кубом, поэтому центральной фигурой для него должен быть куб. Фигура 1&умножение на 2&умножение на 2 в центре нарушило бы симметрию.
Это означает, что у нас есть 6 желтых и 3 − 1 = 2 розовых элемента для создания нескольких идентичных строительных блоков.
Сколько строительных блоков мы должны попытаться создать?
Строительные блоки должны образовывать кубоид за вычетом центральной части. Таким образом, количество желтых частей в строительном блоке должно быть делителем 6 (общее количество желтых блоков), а количество розовых частей строительного блока должно быть разделено на 2 (количество розовых кубов, оставшихся после резервирования одного для центра).
Таким образом, число N одинаковых строительных блоков является наибольшим общим делителем числа одинаковых частей, здесь 6 и 2, что равно НОД(6,2) = 2. Итак, мы должны создать строительный блок из 2 / 2 = 1 розового куба и 6 / 2 = 3 желтых блоков. Так мы и поступили.
Обобщите математический алгоритм, чтобы использовать его для более крупных головоломок.
Для нечетного контейнера:
- Выровняйте лишние части, чтобы убедиться, что они не перекрываются ни в одном слое. Они должны связать один угол контейнера с противоположным углом контейнера. Если нечетные кусочки являются кубиками, они образуют диагональ. Если нечетные фигуры больше (1х1х3), то они образуют непрямую диагональ.
- Если есть только один вид ровных штук, то используйте их для наполнения емкости.
- Если есть разные виды четных штук:
- Отложите в сторону центральный нечетный кусок. Из оставшихся фигур найти наибольший общий делитель N из числа фигур разных типов. N — количество строительных блоков.
- Создайте N одинаковых строительных блоков и соедините их вместе с центральным элементом в случае нечетного контейнера.
В то время как небольшие головоломки можно легко решить методом проб и ошибок, эта стратегия не работает для больших головоломок. Наше исследование четных и нечетных фигур выявляет важную причину: размещение нечетных фигур имеет решающее значение, так как существует очень мало способов их правильного размещения. Используя метод проб и ошибок, можно ошибиться в самом начале и понять, что что-то пошло не так, только после того, как расставишь много фигур. Это невероятно затрудняет определение причины ошибки, поэтому нет пригодной для использования обратной связи; Метод проб и ошибок не эффективен для больших контейнеров. Требуется мышление.
Упаковка только одним типом места
В этом разделе мы рассмотрим размеры кубоидов, которые могут быть сформированы из одного типа кусочка. Это теоретический раздел, который не нужен для решения описанных выше головоломок. Этот раздел не требует сложной математики.
Имея достаточное количество 1&умножения1&умножения1 штуки, мы можем легко сформировать кубоид любого размера. Но как насчет других фигур, таких как 2× 3× 4 или 1× 2× 5 штук? Есть два основных вопроса, которые необходимо исследовать. Во-первых, учитывая длину куска и длину кубоида, как мы можем определить, может ли кубоид быть создан из копий кусочка? Во-вторых, как мы можем, отталкиваясь от одного кусочка, получить длины кубоида, которые могут быть сформированы? В этом разделе мы рассмотрим более простые вопросы, исследуя эти две важные проблемы.
Может ли кубоид 2× 6× 10 быть сформирован только из 1× 2× 5 штук?
ДА! Три фигуры 1× 2× 5 можно расположить рядом, чтобы сформировать форму 1× 6× 5 (3 × 2 = 6). Затем мы можем создать вторую фигуру 1× 6× 5 и объединить их в фигуру 1× 6× 10. Наконец, две фигуры 1× 6× 10 можно поместить вместе, чтобы сформировать кубоид 2× 6× 10.
Можно ли сформировать кубоид 10× 12× 14, используя только кусочки размера 2× 5×6?
Подсказка
Нет необходимости представлять, как бы были расставлены фигуры.
Еще один намек?
Фигура 2× 5× 6 такая же, как фигура 5× 6× 2, поскольку ее можно вращать.
Ответ
ДА. Поскольку 10 / 5 = 2, 12 / 6 = 2, а 14 / 2 = 7, больший кубоид можно рассматривать как 2&умноженное на 2&умноженное на 7 расположение 5&умноженных на 6&умноженных на 2 кусочка. Все 5×6×2 штуки могут быть размещены в одной и той же ориентации.
Как мы можем обобщить эти выводы?
Предположим, что у нас есть только куски размера x × y × z. Тогда построение кубоида X × Y × Z возможно, если существуют положительные целые числа A, B, C , такие, что Ax, By и Cz равны X, Y и Z в некотором порядке.
Сколько штук будет использовано в этом случае?
Мы можем расположить части А в одном направлении, В — в другом, а С — в третьем. В общей сложности будет использовано A × B и times C штук.
Почему Ax, By и Cz могут быть равны X, Y и Z в любом порядке?
Контейнер размером X & умножить на Y & умножить на Z — это то же самое, что и кубоид Z & умножить на X и умножить на Y . Порядок длин не имеет значения, потому что кубоид можно вращать.
Верно ли, что любой кубоид, образованный из 1× 2× 3 pieces, должен иметь длины A, B × 2, C & times 3 для некоторых положительных целых чисел A, B, C ?
НЕТ. Если все 1× 2× 3 штуки ориентированы в одном направлении, кубоид будет иметь размер A × (B × 2) × (C × 3). Но фигуры могут быть ориентированы по-разному и все равно образовывать кубоид. Например, кусочки 1× 2× 3 могут образовать кубоид 1× 5× 6, хотя 1, 5 и 6 не равны A, B × 2 и C & times 3 в любом порядке. Другим примером является пазл "1× 7× 10 1", который состоит из 1× 2× 5 частей.
Какова связь между длинами фигуры и длинами кубоида в этих двух примерах?
В обоих этих примерах одна из длин кубоида является суммой двух длин кусочка. Другая длина кубоида — это НОК (наименьшее общее кратное) тех же двух длин куска. В случае кубоида 1×5×6, образованного из 1× 2× 3 штук, мы имеем 1× 5× 6 = 1 × (2 + 3) × LCM(2,3). Аналогично, 1× 7× 10 = 1 × (2 + 5) × LCM(2,5).
Как мы можем использовать этот факт, чтобы найти способ получения длин кубоидов, которые могут быть построены из данного куска?
Мы начнем с представления длины фигуры в виде упорядоченной тройки. Например, фигура 1× 2×3 представлена как (1, 2, 3). Теперь есть 3 операции, которые мы можем выполнять многократно, чтобы получить длины кубоидов, которые могут быть сформированы из этого кусочка. К ним относятся:
- Измените порядок длины. Это известно как перестановка. В нашем случае он представляет собой вращение в трехмерном пространстве. В качестве примера можно привести
(1, 2, 3) → (2, 3, 1). - Умножьте длины на положительные целые числа A, B и C соответственно. Это соответствует формированию большего кубоида путем размещения частей А в одном направлении, В в другом, а С в третьем направлении. Например, мы можем умножить на 1, 4 и 3, чтобы получить (1, 2, 3) → (1 & умножить на 1, 4 & умножить на 2, 3 & умножить на 3) = (1, 8, 9).
- Возьмите две длины и замените одну на их сумму, а другую на их НОК. Это соответствует формированию более крупного кубоида с кусочками, ориентированными в разных направлениях. Например, выбрав длины 2 и 3, мы получим (1, 2, 3) → (1, 2 + 3, LCM(2,3)) = (1, 5, 6).
Можно ли соединить кусочки4-м способом, чтобы получить кубоид, форма которого отличается от результата3-й операции?
ДА. Рассмотрим кусок размером x × y × z. Третья операция дает кубоид размером x × (y + z) × LCM(y,z), где одна длина x неизменна от фигуры к кубоиду.
Похожим, но другим способом было бы снова поставить ЖКМ(y,z)/y много фигур рядом друг с другом, а ЛКМ(y,z)/y много фигур рядом друг с другом, как и раньше, но теперь повернуть один набор на 90° так, чтобы два блока имели одинаковую длину LCM(y,z), но разную высоту. В математических терминах мы не присоединяем x × y × LCM(y,z) и x × z × LCM(y,z) для получения x × (y + z) × LCM(y,z). Вместо этого один из них, скажем, x × z × LCM(y,z), поворачивается в z × x × LCM(y,z), а затем присоединяется.
Тогда прямоугольная базовая площадь равна не (y + z) × LCM(y,z), а скорее (x + z) × LCM(y,z). Тогда два строительных блока x × y × LCM(y,z) и z × x × LCM(y,z) имеют длины x и z, соответственно, в направлении X.
Складывая ЖКМ(x,z)/x много строительных блоков высоты x и LCM(x,z)/z много строительных блоков высоты z, оба стека достигают высоты LCM(x,z). Когда они присоединены, в результате получается кубоид размером LCM(x,z) × (x + z) × LCM(y,z), который имеет другую форму и размер, чем любой кубоид, полученный в результате третьей операции.
Можно повторять эти операции в любом порядке, сначала создавая кубоид из кусочка, а затем используя кубоид в качестве «кусочка» для создания еще большего кубоида. Ранее мы обсуждали, как кубоид 2× 6× 10 может быть сформирован из 1× 2× 5 штук. В этом случае нужна только одна операция, умножающая на 2, 3 и 2 соответственно: (1, 2, 5) → (2 × 1, 3 × 2, 2 × 5) = (2, 5, 10).
Таким образом, куски размера x × y × z могут не только построить кубоиды размера Ax × By × Cz, но, например, также с размером x × (y + z) × LCM(y,z), где LCM(y,z) — наименьшее общее кратное y и z. Сложив несколько таких строительных блоков вместе, мы получим кубоиды размера Ax × B(y + z) + C(LCM(y,z)).
Теперь мы рассмотрим особый тип изделия. Произведение является гармоническим , если каждая из его больших длин делится на следующую меньшую длину. Например, пьеса 1× 2× 6 является гармонической, так как 2 / 1 = 1 и 6 / 2 = 3. Произведение 1&умножить на 4&умножить на 6 не является гармоническим, так как 6 не кратно 4.
Является ли гармоника 1×2× 3 piece?
НЕТ, потому что 3 не делится на 2.
Что делает гармонические элементы особенными в упаковке? Как они соотносятся с нашим обсуждением длин фигур и кубоидов?
Мы уже отмечали, что любая фигура может образовывать кубоид, длина которого кратна длине фигуры. Оказывается, что длины любого кубоида, образованного идентичными гармоническими кусочками, должны быть кратны длине кусочков. То есть, если гармонический фрагмент имеет длины x, y и z, то любой кубоид, образованный из копий этого фрагмента, должен иметь одну длину, делящуюся на x, другую, делимую на y, и третью, кратную на z. Хотя это простое утверждение, доказательство требует концепций, выходящих за рамки данного веб-сайта. Ссылку на доказательство можно найти в разделе "Подтверждение".
Как этот факт согласуется с четырьмя операциями, которые мы обсуждали выше?
Мы можем начать с того, чтобы представить себе произведение как кубоид, образованный из одной копии произведения. Фигура x × y × z также является кубоидом x × y × z . Длины этого кубоида кратны длине кусочка, поскольку каждое число кратно самому себе. Мы покажем, почему четыре метода, которые мы представили, создают кубоиды, длина которых по-прежнему кратна длине кусочка.
- Изменение порядка длин (перестановка): это просто вращение, которое на самом деле не изменяет длины кубоида. Длины кубоида по-прежнему будут кратны длине кусочка.
- Умножение длин кубоида на положительные целые числа: если длины кубоида уже кратны длине кусочка, это не изменится. Они просто станут более крупными мультипликаторами. Если X = Ax кратно x, то DX = DAx также кратно x для любого положительного целого числа D.
- Замена двух длин на их сумму и НОК: вот почему важны гармонические пьесы; Нам нужно будет использовать определение гармонических частей. Предположим, мы начали с гармонической пьесы (x, y, z), из которой уже образовали кубоид (Ax, By, Cz). Порядок длин не имеет значения, так как кубоид можно вращать. Теперь мы выполним третью операцию над любыми двумя длинами кубоида, скажем, Ax и By: (Ax, By, Cz) → (Ax + By, LCM(Ax,By), Cz). Теперь, поскольку произведение (x, y, z) является гармоническим, одна из двух длин x и y кратна другой. Предположим, что y кратно x. Следовательно, By также кратно x, а поскольку Ax также кратен, сумма Ax + By кратна x. Далее, LCM(Ax,By) является наименьшим общим кратным Ax и By, поэтому по определению он кратен By, следовательно, он делится на y. Наконец, Cz, конечно, кратно z. Таким образом, длины нового кубоида (Ax + By, LCM(Ax,By), Cz) по-прежнему кратны длине кусочка.
- А как насчет четвертой операции? Поскольку эта операция аналогична третьей операции, представленный выше аргумент может быть адаптирован для данного случая. Мы оставляем это как упражнение.
Мы показали, что четыре операции, выполняемые многократно в любом порядке над любым гармоническим произведением, приведут к образованию кубоида, длина которого кратна длине произведения. Важно отметить, что в нашем обсуждении третьей операции (и четвертой!) мы полагаемся на то, что произведение является гармоническим. Когда произведение не является гармоническим, аргумент терпит неудачу. В этом ключевое различие между гармоническими и негармоническими произведениями. Для гармонических частей третий и четвертый методы не дают дополнительных форм по сравнению с первыми двумя методами.
В результате, любой кубоид, образованный из гармонических частей, может иметь все части в одной ориентации. Поэтому, если мы пытаемся сформировать кубоид из одинаковых гармонических кусочков, достаточно попробовать расположить их все лицом в одном направлении. Если такой возможности нет, то кубоид вообще не может сформироваться.
Поскольку произведение 1× 2× 2 является гармоническим, любой кубоид, образованный из копий этого произведения, должен иметь длины A, B & умножить на 2 и C & умножить на 2 для некоторых целых чисел A, B и C. На изображении ниже показан кубоид 5× 4×4, образованный 1× 2× 2 штуками, которые имеют одинаковую ориентацию.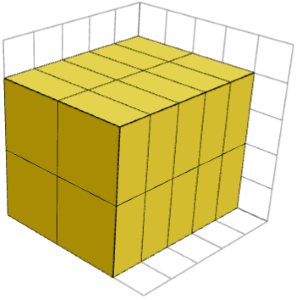
Каковы значения A, B и C ?
Установив A, B × 2 и C × 2 равными 5, 4 и 4 соответственно, мы находим, что A = 5 / 1 = 1, B = 4 / 2 = 2, а C = 4 / 2 = 2.
Должны ли детали быть обращены в одном направлении при упаковке гармоническими элементами?
НЕТ! Хотя всегда возможно, что все детали имеют одинаковую ориентацию, могут быть и другие расстановки, но они не образуют новых форм. На изображении ниже показан другой способ формирования кубоида 5× 4× 4 из 1× 2× 2 штук.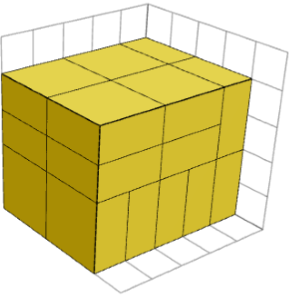
Каковы правила для негармонических произведений?
При работе с негармоническим произведением x × y × z могут быть сформированы некоторые кубоиды, размеры которых не равны Ax × By × Cz для любых целых чисел A, B, C. Например, кубоид 1× 5× 6 можно создать из 1× 2× 3 штук. Это результат третьей операции, о которой говорилось ранее.
Важно отметить, что количество кубиков в кубоиде всегда должно быть кратно количеству кубиков в кусочке. Когда длины куба не кратны разной длине фигуры, одна из длин кубоида будет кратна по крайней мере 2 длинам фигуры в соответствии с третьим и четвертым методами. Этот факт может быть использован для определения того, могут ли определенные кубоиды быть образованы из негармонических кусочков.
Некоторые вопросы для повторения того, что мы исследовали:
Могут ли 2× 4× 12 штук образовать кубоид размера 4× 8× 36 ? А как насчет кубоида размером 10&умно10&умно12 ?
Поскольку 4 / 2 = 2, 8 / 4 = 2, а 36 / 12 = 3, может образоваться кубоид 4× 8× 36.
Одна из длин кубоида 10&умно-10&умно-12 делится на 12. Другие длины — 10 и 10, ни одна из которых не делится на 4. Следовательно, длины кубоида 10× 10× 12 не кратны длине кусочка. Поскольку 12 / 4 = 3 и 4 / 2 = 2, то кусок является гармоническим, следовательно, кубоид 10× 10× 12 не может быть образован из кусочков размера 2× 4× 12.
Могут ли кусочки размером 1&умножить на 3&умножение5 образовать кубоид размера 2&умножить на 15&умножение8 ? А как насчет кубоида 3× 9× 14?
Поскольку число 5 не делится на 3, произведение не является гармоническим. Мы не можем применять наши знания гармонических пьес.
С помощью этих кусочков можно сформировать кубоид 2× 15× 8. Три фишки 1× 3× 5 могут образовать форму 1× 3× 15 (или 1× 15× 3) фигуры, а 5 фигур, расположенных по-разному, могут образовать форму 1× 15× 5. Эти две формы могут быть использованы для создания кубоида 1× 15× 8, две из которых могут образовывать кубоид 2× 15× 8. Мы можем использовать рассмотренные нами операции для более краткости: (1, 3, 5) → (1, 3 + 5, LCM(3,5)) = (1, 8, 15) → (2, 8, 15) → (2, 15, 8).
Когда 1&умножить на 3&умножение на 5 штук объединяется, общее количество кубиков кратно 5. Поскольку 3 × 9 × 14 не делится на 5, кубоид 3× 9× 14 не может быть создан из кусочков размером 1× 3× 5.
Краткое изложение правил для гармонических и негармонических пьес
Вот обзор того, что мы узнали:
- Если длины кубоида кратны длине кусочка, то он может быть образован из копий этого кусочка, независимо от того, является ли произведение гармоничным. Такие кубоиды могут быть сформированы со всеми частями в одной и той же ориентации, но могут также существовать расстановки, в которых фигуры имеют различную ориентацию.
- Если произведение является гармоничным, то любое кубоидное образование должно иметь длину, кратную длине произведения. В результате, любой кубоид, образованный из гармонических частей, может иметь все части в одной и той же ориентации, хотя это не всегда необходимо.
- Если произведение не является гармоническим, то могут быть сформированы кубоиды, длина которых не кратна длине произведения (см. третью и четвертую операции). В этом случае все части не могут иметь одинаковую ориентацию. Используя негармонические элементы, можно создавать кубоиды различной формы, используя 4 метода, описанных ранее.
Справедливы ли эти наблюдения только в трех измерениях?
НЕТ. В этом контексте нет ничего особенного в 3 измерениях. Фактически, установка одной из длин равной 1 эквивалентна уменьшению задачи до 2 измерений. Результаты также действительны более чем в 3 измерениях. Например, пьеса 1×3× 12× 24 является гармонической. Следовательно, любой двумерный кубоид, образованный из этих четырехмерных частей, должен иметь размеры A, B & умножить на 3, C & умножить на 12 и D & умножить на 24 для некоторых положительных целых чисел A, B, C и D.
Как получить практические пазлы?
Мы не можем рассказать вам, как сделать 4-х мерные изделия :) Но в 3-мерном формате, если у вас много запасных кубиков, вы можете соединить их скотчем, чтобы сформировать кусочки.
Вместо коробки 5× 5× 5 можно использовать, например, коробку из-под обуви. Если держать его по диагонали, фигуры останутся на своих местах.
Некоторые из головоломок имеют высоту 1 (например, «1&умножить 7&умно10 1») и поэтому являются двухмерными головоломками. Можно вырезать прямоугольники из миллиметровой бумаги, чтобы использовать их в качестве деталей для этих пазлов.
Признание
Наш интерес к упаковке пазлов разгорелся, когда мы увидели деревянную версию пазла "5x5x5 1" на математической выставке. Вслед за его автором, известным математиком Джоном Хортоном Конвеем, мы нашли от него головоломки «3x3x3 2», «5x5x5 2», а также «5x5x5 3».
Раздел «Упаковка только одним типом деталей» был вдохновлен работами голландского математика де Брёйна. Чтобы узнать больше о наблюдениях де Брёйна по упаковке прямоугольных деталей, обратитесь к этой статье. Вы можете прочитать доказательство де Брёйна о свойствах гармонических пьес здесь.
Следите за обновлениями или подписывайтесь на них: