Paketləmə©
Bu puzzle qalib gəldi/oynadı: 16279/24796

 Niyə bu "Düşünmək üçün yemək" oxumalıyam?
Niyə bu "Düşünmək üçün yemək" oxumalıyam?
Çünki sən təəccüblənəcəksən.
 Bir neçə yığcam tapmacanı sınaqdan keçirəndən sonra, sizcə riyaziyyatın hansı sahəsi onların həlli üçün ən faydalıdır:
Bir neçə yığcam tapmacanı sınaqdan keçirəndən sonra, sizcə riyaziyyatın hansı sahəsi onların həlli üçün ən faydalıdır:
1) Algebra, 2) Ehtimal nəzəriyyəsi, 3) Geometriya, 4) Say nəzəriyyəsi, 5) Simmetriya, 6) Başqa sahə?
Ən faydalı olan şey rəqəmlərin divisibilitliyi, xüsusilə 2 ilə divisibility haqqında düşünməkdir. Bu, Say nəzəriyyəsinin mövzusudur. Yığdığımız şeylər geometrik obyektlərdir, lakin bu o demək deyil ki, tapmacaları həll etmək üçün geometrik biliklər lazımdır. Geometriyadan kvadrat və ya düzbucaqlının sahəsinin nə olduğunu bilməliyik, amma daha heç nə yoxdur.
Bəzi tapmacalar üçün simmetriya haqqında düşünmək də çox faydalıdır.
 Cəld işarələr
Cəld işarələr
Bunlar kömək istəyənlər, lakin riyazi mənşəyi ilə maraqlanmayan şəxslər üçün işarələrdir.
- Hər tapmaca üçün "Bu tapmaca qalib gəldi/oynadı" yanındakı rəqəmlərə baxaraq, hansının ən asan olduğunu yoxlayın. Ən asan tapmacalardan başlamaq həmişə yaxşı fikirdir. İnterface ilə məşğul olmaqla məşq etmək imkanı verəcək.
- "2×3×3 1" və "2×3×3 2" tapmacaları sınaq və xəta ilə asanlıqla həll edilir.
- "1×7×10 1" tapmacası üzərində ilk cəhdiniz uğurlu deyilsə, növbəti tryanızda parçaları döndür.
- "1×7×7 1" – simmetriya haqqında düşünməyin kömək etdiyi tapmacadır. Səbəb qabın (grid) 4 bərabər uzun tərəfli kvadrat bazis olmasıdır. Bizdə isə eyni formaya malik 4 uzun parça var. Buna görə də onları simmetrik şəkildə yerləşdirmək lazımdır. Burada yalnız bir bənövşəyi kvadrat formalı parça vardır. 90° fırlanma simmetrik həllinə malik olmaq üçün bu parça ortada olmalıdır. Hər hansı bir yer həllin 90° simmetriyasını pozardı.
- Qaranlıq düymələri olan tapmacalar daha çox düşünmək tələb edir. 5×5×5 tapmacalara doğru irəliləməzdən əvvəl "3×3×3 2" tapmacalarını tam başa düşməklə başlayın.
 Bu tapmacaları sınaq və səhvsiz necə həll etmək olar?
Bu tapmacaları sınaq və səhvsiz necə həll etmək olar?
Bəzi işarələr bunlardır:
- Çətin problemi daha asan olanlara, yəni alt məqsədlərə bölün. Məsələn, bütün qabı doldurmaq üçün hər bir layı doldurmaq lazımdır.
- Parçaları simmetrik üsulla düzün, xüsusilə də əgər konteyner 3×3×3 kubu və ya 1×7×7 kvadrat formalı qab kimi simmetrikdirsə.
- Verilən məlumatlardan daha çox istifadə edin. Parçaların ölçüləri hansılardır? Onlardan neçəsi eyni formaya malikdir?
Bu "Düşünmək üçün qida" qalan bütün tapmacaları sınaq və xətasız həll etmək məqsədi güdür. Bunun yerinə sadə suallar gəlməklə və onları cavablandırmaqla.
 Təriflər
Təriflər
Aydınlıq üçün paketləmə problemlərini müzakirə etmək üçün istifadə edəcəyimiz bir neçə termin var:
 Parça
Parça
Daha böyük bərkimək üçün bir yerə yığılacaq formalardan biri.
Qəribə bir parça, 1×1×1 parçası və ya 1×3×5 parçası kimi uzunluqları qəribə olan bir parçadır.
Bir parça ən azı iki hətta uzunluğu olsa belə, məsələn, 1×2×4 və ya 2×2×2.
 Bütün parçalar ya hətta, ya da qəribədir?
Bütün parçalar ya hətta, ya da qəribədir?
XEYR. 1×2×3 kimi tam bir hətta uzunluğa malik olan əsər hər iki tərifə uyğun gəlmir. Növbəti hissələrdə qəribə və hətta parçalara diqqət edəcəyik.
 Kuboid/Konteyner
Kuboid/Konteyner
Bir kuboid düzbucaqlı prizmadır. Kuboidin boş qabığına aid etmək üçün "konteyner" sözündən istifadə edirik. Biz qabın məzmunu kimi "cuboid"-ə istinad edirik. Bir qab parçalarla doldurulmalıdır və parçalardan kuboid yaradılmalıdır.
 Lay
Lay
Lay - qabın üzünə paralel istiqamətdə qalınlıq 1-in bir dilimidir. 3×4×5 qabının 3 qat ölçüsü 4×5, 4 qat ölçüsü 3×5, 5 qat ölçüsü 3×4-dir.
 1×5×7 qabının neçə qatı var?
1×5×7 qabının neçə qatı var?
Onun bir 5×7 qatı, beş ədəd 1×7 qatı və yeddi ədəd 1×5 qatı vardır. Ümumi olaraq 1 + 5 + 7 = 13 qata malikdir.
 Kub
Kub
Xüsusi olaraq, daha böyük kub deyil, 1×1×1 kub. 1×1×1 parçası 1 kubdan, 1×1×3 parçası isə 1 × 1 × 3 = 3 kubdan ibarətdir.
 Tikinti Bloku
Tikinti Bloku
Bir-birinə bərkidilmiş bir neçə parça bina bloku əmələ gətirir. Maraqlı tikinti blokları simmetriyaya malik olacaq. Daha sərt bulmacalar üçün bir neçə eyni və ya güzgü eynilikli bina blokları plus bir mərkəz parçası konteyneri dolduracaq.
 Strategiya
Strategiya
Çətin problemin həllinin yarısı ağır problemi daha kiçik problemlərə bölməkdir.
Bunu etmək üçün özümüzə sadə suallar verməliyik. Aşağıdakı suallar yığma tapmacaların həllində faydalı olacaq.
 Hər bir kuboid 1×2×2 ölçüdə parçalarla əmələ gələ bilərmi ? Məsələn, 3×3×3 kuboidi yalnız 1×2×2 ölçüsündə olan parçalardan istifadə edərək əmələ gələ bilər ?
Hər bir kuboid 1×2×2 ölçüdə parçalarla əmələ gələ bilərmi ? Məsələn, 3×3×3 kuboidi yalnız 1×2×2 ölçüsündə olan parçalardan istifadə edərək əmələ gələ bilər ?
XEYR. 1×2×2 parçası hətta bir ədəd kubdan ibarətdir. Buna görə də 1×2×2 parçalarının hər hansı bir ədədi birlikdə hətta ümumi kub sayına malik olacaq. 3×3×3 kuboidi qəribə sayda kublardan ibarət olduğundan bu şəkildə əmələ gələ bilməz.
Növbəti bir neçə hissədə, xüsusilə 2 ilə divisibility müəyyən bulmacalar həll etmək üçün parçaların necə yerləşdirilməsini necə müəyyən edəcəyini araşdıracağıq.
 1×2×2 parçaları ən azı 3×3×3 konteynerinin istənilən qatını doldura bilərmi?
1×2×2 parçaları ən azı 3×3×3 konteynerinin istənilən qatını doldura bilərmi?
Bu sualın cavabı yenə də NO-dir. Bir parça ilə tutula bilən təbəqədəki ərazi parçanın üzlərindən birinin sahəsidir, elə deyilmi?
 1×2×2 parçasının üzləri hansılardır?
1×2×2 parçasının üzləri hansılardır?
Bir 1×2×2 parçasının iki cüt paralel 1×2 üzü, bir cüt isə 2×2 üzü vardır.
 Bu üzlüklər hansı sahələrdir və onların ortaq cəhəti nədir?
Bu üzlüklər hansı sahələrdir və onların ortaq cəhəti nədir?
Sahələr 1 × 2 = 2 və 2 × 2 = 4-dür. 2 və 4- hər ikisi hətta ədəddir.
Müşahidə edirik ki, 1×2×2 parçası hər bir qatda yalnız hətta bir ədəd kub (2 və ya 4) tuta bilər.
 Bu, hətta bütün parçalar üçün də doğrudurmu?
Bu, hətta bütün parçalar üçün də doğrudurmu?
Bir parçanın hər üzü iki uzunluğa malikdir. Hətta parçaların da bir-birindən qəribə uzunluğu olduğu üçün üzlərinin hər birinin uzunluğu ən azı bir olacaq. Çünki hətta × odd = hətta, hər üzün sahəsi hətta olacaq. Ona görə də biz onları hətta parça da adlandırırıq!
Öyrəndik ki, qəribə yan uzunluqlara malik olan kuboidlər yalnız parçalardan belə əmələ gələ bilməz. Qəribə sahəyə malik olan təbəqəni hətta parçalarla da doldurmaq mümkün deyil. Buna görə də "3×3×3 2" tapmacasının bir neçə 1×1×1 parçası vardır ki, bu da qəribə parçalardır.
Burada daha bir faydalı sualı nəzərdən keçirmək lazımdır:
 İki növ parçadan biri (1×1×1 və 1×2×2) digərindən daha "qiymətlidirmi"?
İki növ parçadan biri (1×1×1 və 1×2×2) digərindən daha "qiymətlidirmi"?
BƏLI. Əgər bizdə cəmi 1×1×1 parçası olsaydı, o zaman hər hansı bir tapmaca əhəmiyyətsiz olardı. Bu fikirlə razısınızmı? Əgər bizdə cəmi 1×2×2 parça olsaydı, onda yuxarıda göstərildiyi kimi, qəribə bir qab doldurmaq mümkün deyildi.
Açıq-aşkar sual: 3×3×3 qabını doldura bilən 1×1×1 parçalarının minimum sayı nə qədər olar?
Təbii ki, aşağıdakı suallar meydana çıxır:
 Niyə üç 1×1×1 parçası kifayətdir?
Niyə üç 1×1×1 parçası kifayətdir?
Bu suala cavab vermək üçün qəribə qatların (qəribə sahəyə malik layların) sayını hətta parçalarla və cəmi 3 kubla doldurmaq mümkün olan qəribə sahə qatlarının sayı ilə müqayisə edəcəyik.
 3×3×3 qabının neçə qatı var?
3×3×3 qabının neçə qatı var?
Üç istiqamətdən hər birində (eni, hündürlüyü, dərinliyi) konteynerin 3 qatı vardır. 3 + 3 + 3 = 9 ədəd qəribə qatlar vardır ki, onlar qab dolduqda doldurulur.
 Bir 1×1×1 parçası (və bəzi hətta 1×2×2 parçaları) ilə neçə qəribə 3×3 layı tamamlana bilər?
Bir 1×1×1 parçası (və bəzi hətta 1×2×2 parçaları) ilə neçə qəribə 3×3 layı tamamlana bilər?
Üç qat: üfüqi təbəqə və 1×1×1 parçasını ehtiva edən iki şaquli təbəqə. Buna görə də 3 kub ən çox 3 × 3 = 9 qat doldurmağa kömək edə bilər.
Bu, 3 kubun lazım olduğunu göstərir. "3×3×2 2" tapmacası həll edilə bildiyi üçün 9 qəribə qatı doldurmaq üçün 3 kub da kifayət edir.
 Bu bizə 3 kubun yerləşdiyi yer haqqında nə deyir?
"3×3×3 2" puzzle?
Bu bizə 3 kubun yerləşdiyi yer haqqında nə deyir?
"3×3×3 2" puzzle?
9 qatların hər birində 0 deyil, yalnız 1 kub ola bilər və 2 kub deyil! Əks halda 9 qat üçün 3 kub kifayət etməzdi.
Bu, həll üçün kəşfdir. Bundan başqa, kubları yerləşdirməyin yeganə yolu diaqonal boyunca - bir kubu mərkəzdə, digər iki kub isə diaqonal əks künclərdə yerləşir. Əks halda, bulky 1×2×2 parçaları 3 kub ətrafında boşluğu doldurmaq üçün çox böyük olardı.
Buna görə də bir kübrəni bir küncə, üç 1×2×2 parçasını isə həmin küpün ətrafında simmetrik şəkildə yerləşdirin. Bir kubu mərkəzə, birini əks küncə qoyun, qalanları aydın olacaq.
 Bu vəziyyətdən daha nə öyrənə bilərik? Məsələn, onun simmetriyası varmı?
Bu vəziyyətdən daha nə öyrənə bilərik? Məsələn, onun simmetriyası varmı?
Simmetriyalar küncə birinci kübrəni və onun ətrafına üç 1×2×2 parçasını qoyduqdan sonra görünür. Həllolmanın 120° fırlanan simmetriyası var. Kubun diaqonalı fırlanan müstəvi kimi (120° = 1/3 tam dairənin fırlanması) olur.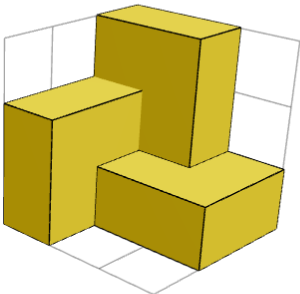
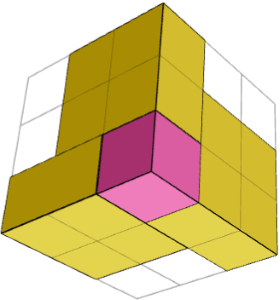
 Həll eyni və ya simmetrik bina bloklarının cəmidirmi? Hər biri bir neçə hissədən ibarətdir?
Həll eyni və ya simmetrik bina bloklarının cəmidirmi? Hər biri bir neçə hissədən ibarətdir?
BƏLI. Kuboid — güzgü simmetrik (1 kub bir küncdə + üç 1×2×2 parçası onun ətrafında) və ortasında bir kub olan 2 bina bloklarının cəmidir. Yuxarıdakı 2 görüntüdə 2 tərəfdən bir bina bloku göstərilir.
 Müxtəlif tikinti blokları istifadə edərək bu puzzle həll etmək üçün başqa bir yol var?
Müxtəlif tikinti blokları istifadə edərək bu puzzle həll etmək üçün başqa bir yol var?
BƏLI. Aşağıdakı sol və sağ şəkillərdə "3×3×3 2" tapmacası üçün iki güzgü simmetrik bina bloku göstərilir. Onları tapmacanı həll etmək üçün mərkəz kubu (orta görüntü) ilə birləşdirmək olar.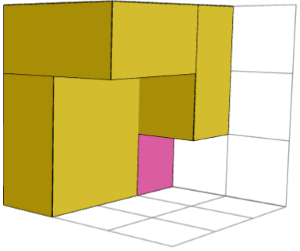
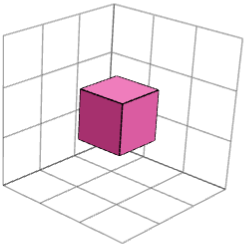
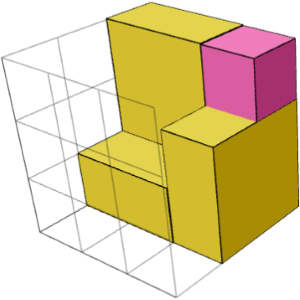
 Nəyə görə tikinti blokları barədə düşünmək bizi narahat etməlidir?
Nəyə görə tikinti blokları barədə düşünmək bizi narahat etməlidir?
Kiçik verilmiş parçalardan istifadə etmək və onlardan simmetrik bir şey yaratmaq daha asandır, nəinki daha böyük qabı bütün parçalarla doldurmaq.
 "3×5×7 1" kimi daha böyük tapmacaların həlli üçün tikinti bloklarından istifadə etmək olarmı ?
"3×5×7 1" kimi daha böyük tapmacaların həlli üçün tikinti bloklarından istifadə etmək olarmı ?
BƏLI. Daha böyük qablar, hətta onların uzunluqları bir-birindən fərqli olsa belə, eyni/güzgü simmetrik tikinti blokları vasitəsilə doldurula bilər. "3×5×7 1" puzzle həll etmək üçün bir çox yolları var bina blokları və bir mərkəz qəribə parça istifadə edərək. Bəzi nümunələri tapmaq üçün onu sizə buraxırıq.
 Hansı parçaların tikinti bloklarını təşkil etməli olduğunu haradan bilirik?
Hansı parçaların tikinti bloklarını təşkil etməli olduğunu haradan bilirik?
Əvvəlcə qəribə bir kuboidin mərkəzi haqqında düşünək. Mərkəz mövqeyi unikal olduğu üçün, əgər biz simmetrik həll istəyiriksə, mərkəzi konteyner ilə eyni formaya malik parça ilə məşğul olmalıdır. 3×3×3 cuboid bir kub belə ki, bunun üçün mərkəz parça bir kub olmalıdır. Mərkəzdəki 1×2×2 parçası simmetriyanı sındırardı.
Bu o deməkdir ki, bir sıra eyni tikinti bloklarını inşa etmək üçün bizdə 6 sarı və 3 − 1 = 2 çəhrayı parçalar var.
 Neçə tikinti bloku yaratmağa çalışmalıyıq?
Neçə tikinti bloku yaratmağa çalışmalıyıq?
Bina blokları mərkəz parçasını kuboid minus təşkil etməlidir. Buna görə də, bina blokunda sarı parçaların sayı 6 ədəd divisor olmalıdır (sarı blokların ümumi sayı) və bina blokunun çəhrayı parçalarının sayı 2-ni bölməlidir (mərkəz üçün rezerv etdikdən sonra qalan çəhrayı kubların sayı).
Beləliklə, eyni adlı bina bloklarının N ədədi eynicinsli parçaların sayının ən böyük ümumi divisordur, burada 6 və 2, hansı ki, GCD(6,2) = 2. Beləliklə, biz 2 / 2 = 1 çəhrayı kub və 6 / 2 = 3 sarı blokdan bina bloku yaratmalıyıq. Biz də belə etdik.
 Riyazi alqoritmi daha böyük tapmacalar üçün istifadə etmək üçün yekunlaşdırın.
Riyazi alqoritmi daha böyük tapmacalar üçün istifadə etmək üçün yekunlaşdırın.
Qəribə qab üçün:
- Hər hansı bir qatda üst-üstə düşməmələrini yoxlamaq üçün qəribə parçaları nizamlayın. Onlar qabın bir küncündə qabın əks küncünə bağlanmalıdırlar. Əgər qəribə parçalar kubdursa, onlar diaqonal əmələ gətirir. Əgər qəribə parçalar daha böyükdürsə (1x1x3), onda onlar düz olmayan diaqonal əmələ gətirirlər.
- Əgər yalnız bir növ hətta parça varsa, onda onlardan istifadə edərək qabı doldurun.
- Hətta parçaların müxtəlif növləri varsa:
- Orta qəribə parçanı bir kənara qoyun. Qalan parçalardan müxtəlif tiplərin ədədlərinin ən böyük ümumi divisor N-ni tapın. N – tikinti bloklarının sayıdır.
- N eyni adlı tikinti bloklarını yaradın və qəribə bir qab halında onları mərkəz parçası ilə bir araya qoyun.
Kiçik tapmacalar sınaq və xəta ilə asanlıqla həll olunsa da, bu strategiya daha böyük tapmacalar üçün yaramır. Bizim qəribə və hətta parçaların tədqiq edilməsi vacib bir səbəbi aşkar edir: qəribə parçaların yerləşdirilməsi olduqca vacibdir, çünki onların düzgün yerləşdirilməsinin çox az yolu var. Sınaq və xətadan istifadə edərək, başlanğıcda səhv etmək və yalnız bir çox parçaları qoyduqdan sonra bir şeyin səhv olduğunu anlamaq olar. Bu, xətanın səbəbini müəyyən etməyi olduqca çətinləşdirir, buna görə də heç bir istifadə edilə bilən rəy yoxdur; sınaq-xəta metodu daha böyük qablar üçün effektiv deyil. Düşünmək tələb olunur.
 Yalnız bir növ parça ilə yığılma
Yalnız bir növ parça ilə yığılma
Bu bölmədə bir növ parçadan əmələ gələ bilən kuboidlərin ölçülərini araşdıracağıq. Bu, yuxarıdakı tapmacaların həlli üçün lazım olmayan nəzəri hissədir. Bu bölmə çətin riyaziyyat tələb etmir.
Kifayət qədər 1×1×1 parçaları ilə asanlıqla istənilən ölçüdə kuboid əmələ gətirə bilərik. Bəs 2×3×4 və ya 1×2×5 parçaları kimi digər parçalar haqqında nə demək olur? Araşdırma aparmaq üçün iki əsas sual var. İlk öncə , bir parçanın uzunluğunu və kuboidin uzunluğunu nəzərə alsaq, kuboidin parçanın nüsxələrindən yaradıla biləcəyini necə müəyyən edə bilərik? İkincisi, biz, bir parçadan başlayaraq, əmələ gələ biləcək bir kuboidin uzunluqlarını necə meydana gətirə bilərik? Bu bölmə boyunca bu iki vacib problemi araşdırarkən daha sadə sualları nəzərdən keçirəcəyik.
 2×6×10 kuboidi yalnız 1×2×5 parçasından əmələ gələ bilərmi?
2×6×10 kuboidi yalnız 1×2×5 parçasından əmələ gələ bilərmi?
BƏLI! Üç 1×2×5 parçasını 1×6×5 formasını (3 × 2 = 6) əmələ gətirmək üçün yan-yana yerləşdirmək olar. Sonra ikinci 1×6×5 formasını yarada və onları 1×6×10 şəklində birləşdirə bilərik. Nəhayət, iki 1×6×10 formasını bir yerdə yerləşdirmək olar ki, 2×6×10 kuboidi əmələ gətirə bilər.
 10×12×14 kuboidinin yalnız ölçüsü 2×5×6 parçalarından istifadə edərək yaranması mümkündürmü ?
10×12×14 kuboidinin yalnız ölçüsü 2×5×6 parçalarından istifadə edərək yaranması mümkündürmü ?
 Işarə
Işarə
Parçaların necə düzüləcəyini təsəvvür etmək lazım deyil.
 Başqa bir işarə?
Başqa bir işarə?
Bir 2×5×6 parçası, 5×6×2 parçası ilə eynidir, çünki onu dönə bilər.
 Cavab
Cavab
BƏLI. 10 / 5 = 2, 12 / 6 = 2 və 14 / 2 = 7-dən etibarən daha böyük kuboidi 5×6×2 parçalarının 2×2×7 düzülüşləri hesab etmək olar. 5×6×2 parçalarını hamısı eyni oriyentirlə yerləşdirmək olar.
 Bu tapıntıları necə ümumiləşdirə bilərik?
Bu tapıntıları necə ümumiləşdirə bilərik?
Fərz edək ki, x × y × z ölçüdə yalnız parçalarımız var. Sonra X × Y × Z cuboid inşa əgər müsbət integers A, B, C belə varsa, mümkün ki, Ax, By və Cz bərabər X, Y və Z müəyyən qaydada.
 Bu halda neçə parçadan istifadə olunacaq?
Bu halda neçə parçadan istifadə olunacaq?
A parçalarını bir istiqamətdə, B-ni digər istiqamətdə, C-ni isə üçüncü istiqamətdə düzüb-düzə bilərik. Ümumilikdə A × B × C parçalarından istifadə olunacaq.
 Ax , By və Cz nəyə görə X, Y və Z-yə hər hansı bir qaydada bərabər ola bilər?
Ax , By və Cz nəyə görə X, Y və Z-yə hər hansı bir qaydada bərabər ola bilər?
Ölçüsü X × Y × Z olan bir konteyner bir Z × X × Y cuboid ilə eynidir. Uzunluqların sırası heç bir əhəmiyyət kəsb etmir, çünki kuboidi fırlada bilər.
 Doğrudurmu ki, 1×2×3 parçalarından əmələ gələn hər hansı bir kuboid A, B × 2, C × 3 uzunluqları olmalıdır, bəzi müsbət integers A, B, C ?
Doğrudurmu ki, 1×2×3 parçalarından əmələ gələn hər hansı bir kuboid A, B × 2, C × 3 uzunluqları olmalıdır, bəzi müsbət integers A, B, C ?
XEYR. Əgər bütün 1×2×3 parçaları eyni istiqamətdə yönələrsə, kuboid A × ölçüsünə (B × 2) × (C × 3) malik olacaq. Lakin parçaları fərqli şəkildə istiqamətləndirib, yenə də kuboid əmələ gətirə bilər. Məsələn, 1×2×3 parçaları 1,5 və 6 A, B × 2 və C × 3-ə hər hansı bir qaydada bərabər olmasa da, 1×5×6 kuboid əmələ gətirə bilər. Digər bir misal isə 1×2×5 parçasından ibarət olan "1×7×10 1" tapmacasıdır.
 Bu iki nümunədə parçanın uzunluqları ilə kuboidin uzunluqları arasındakı əlaqə nədir?
Bu iki nümunədə parçanın uzunluqları ilə kuboidin uzunluqları arasındakı əlaqə nədir?
Bu nümunələrin hər ikisində kuboidin uzunluqlarından biri parçanın iki uzunluğunun cəmidir. Kuboidin fərqli uzunluğu parçanın eyni iki uzunluğunda olan LCM (Ən Aşağı Ümumi Çoxluq) dır. 1×2×3 parçasından əmələ gələn 1×5×6 kuboidi halında 1×5×6 = 1 × (2 + 3) × LCM(2,3) var. Oxşar şəkildə 1×7×10 = 1 × (2 + 5) × LCM(2,5).
 Bu faktdan istifadə edərək, verilmiş parçadan inşa edilə bilən kuboidlərin uzunluqlarının əmələ gəlməsi yolunu necə tapa bilərik?
Bu faktdan istifadə edərək, verilmiş parçadan inşa edilə bilən kuboidlərin uzunluqlarının əmələ gəlməsi yolunu necə tapa bilərik?
Biz bir parçanın uzunluğunu sifariş edilmiş üçqat kimi təmsil etməklə başlayırıq. Məsələn, 1×2×3 parçası (1, 2, 3) ilə təmsil olunur. İndi isə bu parçadan əmələ gələ biləcək kuboidlərin uzunluqlarını vermək üçün dəfələrlə edə biləcəyimiz 3 əməliyyat var. Onlar bunlardır:
- Uzunluqların sıralarını dəyişin. Bu, permutasiya kimi tanınır. Bizim halda bu, 3-ölçülü fəzada fırlanmanı təmsil edir. Buna misal olaraq
(1, 2, 3) → (2, 3, 1). - A, B və C müsbət inteqrlərlə uzunluqları sıra ilə çoxaldın. Bu, A parçalarını bir istiqamətə, B-ni başqa istiqamətə, C-ni isə üçüncü istiqamət üzrə yerləşdirməklə daha böyük kuboidin əmələ gəlməsi ilə mütənasibdir. Məsələn, (1, 2, 3) → (1 × 1, 4 × 2, 3 × 3) = (1, 8, 9) vermək üçün 1, 4 və 3 ilə çoxala bilərik.
- İki uzunluq götür və birini onların cəmi ilə, birini isə LCM ilə əvəz et. Bu, müxtəlif istiqamətlərə istiqamətlənmiş parçalarla daha böyük kuboidin əmələ gəlməsi ilə mütənasibdir. Məsələn, 2 və 3-cü uzunluqları seçərkən (1, 2, 3) → (1, 2 + 3, LCM(2,3)) = (1, 5, 6) əldə edərdik.
 3 rd əməliyyatının nəticəsindən forması fərqli olan kuboid istehsal etmək üçün parçaları4-cü yolla birləşdirmək olarmı?
3 rd əməliyyatının nəticəsindən forması fərqli olan kuboid istehsal etmək üçün parçaları4-cü yolla birləşdirmək olarmı?
BƏLI. X × y × z ölçüsündə bir parçanı nəzərdən keçirək. Üçüncü əməliyyatda x × (y + z) × LCM(y,z) ölçülü kuboid hasil edilir. Burada bir uzunluq x parçadan kuboidə dəyişməzdir.
Oxşar, lakin fərqli bir yol yenə LCM(y,z)/y bir-birinin yanında bir çox parça qoymaq və LCM(y,z)/y bir-birinin yanında bir çox parçalar qoymaq olardı, əvvəlki kimi, indi isə bir seti 90° ilə döndürmək üçün ki, iki blok eyni uzunluqda LCM(y,z), lakin müxtəlif hündürlüklərə malik olsun. Riyazi baxımdan x × y × y × LCM(y,z) və x × z × z × LCM(y,z) x × (y + z) × LCM(y,z) əmələ gətirmək üçün ilişdirmirik. Əksinə, onlardan biri, deyək ki, x × z × LCM(y,z), z × x × LCM(y,z) və sonra bərkidilir.
Düzbucaqlı baza sahəsi o zaman (y + z) × LCM(y,z) deyil, əksinə (x + z) × LCM(y,z) olur. Sonra iki tikinti bloku x × y × LCM(y,z) və z × x × LCM(y,z) uzunluqları x və z, müvafiq olaraq, X istiqamətində olur.
LCM(x,z)/x bir çox bina blokları hündürlük x və LCM(x,z)/z bir çox bina blokları hündürlük z, hər iki yığın hündürlük LCM(x,z) çatır. Onlar bərkidildikdə nəticə LCM(x,z) × (x + z) × LCM(y,z) ölçüsündə kuboid olur. Bu kuboid üçüncü əməliyyatdan irəli gələn hər hansı bir kuboiddən fərqli forma və ölçüyə malikdir.
Bu əməliyyatları istənilən qaydada təkrarlamaq olar. Əvvəlcə parçadan kuboid əmələ gətirmək, sonra isə kuboiddən "parça" kimi istifadə edərək daha da böyük bir kuboid əmələ gətirmək olar. 2×6×10 kuboidin 1×2×5 parçasından necə əmələ gələ biləcəyini daha əvvəl müzakirə etdik. Bu halda yalnız bir əməliyyat lazımdır, müvafiq olaraq 2, 3 və 2 ilə çoxalır: (1, 2, 5) → (2 × 1, 3 × 2, 2 × 5) = (2, 5, 10).
Beləliklə, ölçüsü x × y × z parçaları yalnız ölçülərin kuboidlərini inşa edə bilmir Ax × By × Cz, həm də məsələn, ölçüsü x × (y + z) × LCM(y,z), burada LCM(y,z) y və z-nin ən aşağı ümumi çoxluğudur. Bu tikinti bloklarından bir neçəsinin bir yerə qoyulması, ölçüsünə görə kuboidləri Ax &y + z) + C(LCM(y,z)) verir.
İndi biz əsərin xüsusi növünü nəzərdən keçirəcəyik. Bir parça harmonikdir , əgər onun daha böyük uzunluqlarının hər biri növbəti kiçik uzunluqla parçalanırsa. Məsələn, 1×2×6 parçası 2 / 1 = 1 və 6 / 2 = 3-cü ildən harmonikdir. 1×4×6 parçası harmonik deyil, çünki 6 4-dən çox deyil.
 1×2×3 parçası harmonikdirmi?
1×2×3 parçası harmonikdirmi?
XEYR, çünki 3 2 ilə parçalanmadır.
 Harmonik parçaları yığmada xüsusi edən nədir? Onlar parça və kuboidlərin uzunluğunu müzakirəmizlə necə bağlıdır?
Harmonik parçaları yığmada xüsusi edən nədir? Onlar parça və kuboidlərin uzunluğunu müzakirəmizlə necə bağlıdır?
Artıq müşahidə etdik ki, istənilən parça parçanın uzunluğunun çoxluğu olan kuboid əmələ gətirə bilər. Məlum olur ki, eyni harmonik parçalarla əmələ gələn hər hansı bir kuboidin uzunluğu parçaların uzunluqlarının çoxluğu olmalıdır . Yəni, harmonik parçanın uzunluqları x, y və z olarsa, bu parçanın nüsxələrindən əmələ gələn hər hansı bir kuboidin bir uzunluğu x, digərinin divisilləri y, üçüncü divisil isə z ilə olmalıdır. Bu, sadə bir bəyanat olsa da, sübut bu veb-saytın miqyasından kənar anlayışlar tələb edir. Sübutun linkinə "Etiraf" bölməsində rast gəlmək olar.
 Bu fakt yuxarıda müzakirə etdiyimiz 4 əməliyyatla necə üst-üstə düşür?
Bu fakt yuxarıda müzakirə etdiyimiz 4 əməliyyatla necə üst-üstə düşür?
Bir parçanı parçanın bir nüsxəsindən əmələ gələn kuboid kimi düşünməklə başlaya bilərik. Bir x × y × z parçası da x × y × z cuboid. Bu kuboidin uzunluqları parçanın uzunluqlarının çoxluğudur, belə ki, hər ədəd öz-özlüyündə çoxluq təşkil edir. Təqdim etdiyimiz dörd üsulun nəyə görə uzunluqları hələ də parçanın uzunluqlarının çoxluğu olan kuboidlər istehsal etməsinin səbəbini göstərəcəyik.
- Uzunluqların sırasının dəyişdirilməsi (permutasiya): bu sadəcə dönmədir və əslində kuboidin uzunluğunu dəyişmir. Kuboidin uzunluqları hələ də parçanın uzunluqlarının çoxluğu olacaq.
- Kuboidin uzunluqlarını müsbət inteqrlərlə çoxaltmaq: əgər kuboidin uzunluqları artıq parçanın uzunluqlarının çoxluğudursa, bu, dəyişməyəcək. Onlar sadəcə olaraq daha böyük çoxluqlara çevriləcəklər. Əgər X = Ax x çoxluğudursa, onda DX = DAx da x çoxluğudur, hər hansı bir müsbət integer D üçün.
- İki uzunluğun onların cəmi və LCM ilə əvəz edilməsi: bu səbəbdən harmonik parçalar vacibdir; harmonik parçaların tərifini istifadə etmək lazım gələcək. Fərz edək ki, biz harmonik parçadan (x, y, z) başlamışıq. Buradan artıq kuboidi (Ax, By, Cz) əmələ gətirmişik. Uzunluqların sırası heç bir əhəmiyyət kəsb etmir, çünki kuboidi fırlada bilər. İndi biz üçüncü əməliyyatı kuboidin istənilən iki uzunluğunda yerinə yetirəcəyik, ax və By: (Ax, By, Cz) → (Ax + By, LCM(Ax,By), Cz). İndi isə parça (x, y, z) harmonik olduğundan iki uzunluqdan biri x və y- digərinin çoxluğudur. Fərz edək ki, y x çoxluğudur. Bu səbəbdən By da x çoxluğudur və Ax da olduğu kimi, Ax + By çoxluğu da x çoxluğudur. Sonra LCM(Ax,By) ən aşağı ümumi çoxluq ax və By, belə ki, müəyyən bir by çoxluğu ilə, belə ki, y ilə divisible edir. Nəhayət, Cz, əlbəttə ki, z-in çoxluğudur. Buna görə də yeni kuboidin uzunluqları (Ax + By, LCM(Ax,By), Cz) hələ də parçanın uzunluqlarının çoxluğudur.
- Bəs dördüncü əməliyyat haqqında nə demək? Bu əməliyyat üçüncü əməliyyata bənzədiyi üçün yuxarıda təqdim olunan arqument bu hal üçün uyğunlaşa bilər. Biz onu bir məşq kimi tərk edirik.
Biz göstərmişik ki, hər hansı harmonik parça üzərində hər hansı bir qaydada dəfələrlə həyata keçirilən dörd əməliyyat nəticəsində uzunluğu parçanın uzunluqlarının çoxluğu olan kuboid əmələ gələcək. Qeyd etmək lazımdır ki, üçüncü əməliyyatı (və dördüncüsü!) müzakirəmizdə əsərin harmonik olmasına güvənirik. Bir parça harmonik olmadıqda arqument uğursuz olur. Harmonik və qeyri-harmonik parçalar arasındakı əsas fərq budur. Harmonik parçalar üçün üçüncü və dördüncü metodlar ilk iki metodla müqayisədə əlavə formalar əmələ gəlmir.
Nəticədə harmonik parçalardan əmələ gələn hər hansı bir kuboid bütün parçalara eyni oriyentasiyada malik ola bilər. Ona görə də, əgər biz eyni harmonik parçalardan kuboid əmələ gətirməyə çalışırıqsa, onların hamısını eyni istiqamətdə birləşdirməyə çalışmaq kifayətdir. Əgər bu mümkün deyilsə, onda ümumiyyətlə kuboid əmələ gələ bilməz.
Bir 1×2×2 parçası harmonik olduğundan, bu parçanın kopyalarından əmələ gələn hər hansı bir kuboid A, B × 2 və C × 2 bəzi integers A, B və C üçün uzunluğa sahib olmalıdır. Aşağıdakı görüntüdə 1×2×2 parçası ilə əmələ gəlmiş 5×4×4 kuboidi göstərilir. Bu kuboidlərin hamısı eyni oriyentasiyaya malikdirlər.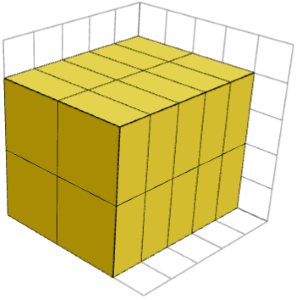
 A, B və C dəyərləri hansılardır ?
A, B və C dəyərləri hansılardır ?
A, B × 2 və C × 2-ni 5, 4 və 4-ə bərabər olaraq təyin etsək, müvafiq olaraq A = 5 / 1 = 1, B = 4 / 2 = 2 və C = 4 / 2 = 2 taparıq.
 Harmonik parçalarla yığılarkən parçalar eyni istiqamətə üz-üzə gəlmək məcburiyyətindədirmi?
Harmonik parçalarla yığılarkən parçalar eyni istiqamətə üz-üzə gəlmək məcburiyyətindədirmi?
XEYR! Baxmayaraq ki, hər zaman bütün parçaların eyni oriyentirə malik olması mümkündür, lakin başqa sazlamalar da ola bilər, lakin onlar yeni formalar əmələ gətirməz. Aşağıdakı şəkildə 1×2×2 parçalarından 5×4×4 kuboidinin əmələ gəlməsi üçün fərqli bir yol göstərilir.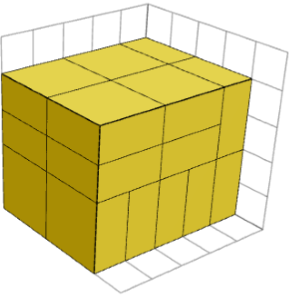
 Qeyri-harmonik parçalar üçün hansı qaydalar var?
Qeyri-harmonik parçalar üçün hansı qaydalar var?
Qeyri-harmonik parça x × y × z ilə işləyərkən bəzi kuboidlər əmələ gələ bilər ki, onların ölçüləri hər hansı bir integers A, B, C üçün Ax × By × Cz deyil. Məsələn, 1×5×6 kuboidi 1×2×3 parçasından yaratmaq olar. Bu, daha əvvəl də müzakirə edildiyi kimi, üçüncü əməliyyatın nəticəsidir.
Qeyd etmək lazımdır ki, kuboiddəki kubların sayı parçadakı kubların sayına görə həmişə divisibl olmalıdır. Kubun uzunluqları hər biri parçanın müxtəlif uzunluqlarının çoxluğu olmadıqda, üçüncü və dördüncü metodlara görə, kuboidin uzunluqlarından biri parçanın ən azı 2 uzunluğundan ibarət ümumi çoxluq olacaqdır. Bu faktdan müəyyən kuboidlərin qeyri-harmonik parçalardan əmələ gələ biləcəyini müəyyən etmək mümkündür.
 Araşdırdıqlarımızı nəzərdən keçirmək üçün bəzi suallar:
Araşdırdıqlarımızı nəzərdən keçirmək üçün bəzi suallar:
 2×4×12 parçaları 4×8×36 ölçüsündə kuboid əmələ gətirə bilərmi ? 10×10×12 ölçüsü olan kuboid haqqında nə demək ?
2×4×12 parçaları 4×8×36 ölçüsündə kuboid əmələ gətirə bilərmi ? 10×10×12 ölçüsü olan kuboid haqqında nə demək ?
4 / 2 = 2, 8 / 4 = 2 və 36 / 12 = 3-dən etibarən bir 4×8×36 kuboidi əmələ gələ bilər.
10×10×12 kuboidinin uzunluqlarından biri 12 ədəd divisibldir. Digər uzunluqları 10 və 10-dır, onların heç biri 4-ə qədər parçalanmadır. Buna görə də 10×10×12 kuboidinin uzunluqları parçanın uzunluqlarının çoxluğu deyil. 12 / 4 = 3 və 4 / 2 = 2 olduğundan parça harmonikdir, buna görə də 10×10×12 kuboidi ölçüsü 2×4×12 olan parçalardan əmələ gələ bilməz.
 1×3×5 ölçüsündə olan parçalar 2×15×8 ölçüsündə kuboid əmələ gətirə bilərmi ? Bəs 3×9×14 kuboidi haqqında nə demək olur?
1×3×5 ölçüsündə olan parçalar 2×15×8 ölçüsündə kuboid əmələ gətirə bilərmi ? Bəs 3×9×14 kuboidi haqqında nə demək olur?
5-i 3-ə parçalanmadığı üçün əsər harmonik deyil. Harmonik parçalar haqqında biliyimizi tətbiq edə bilmərik.
Bu parçalarla 2×15×8 kuboidi əmələ gətirmək mümkündür. Üç 1×3×5 parçası 1×3×15 (və ya 1×15×3) formasını formalaşdıra bilər. Fərqli şəkildə düzülən parçalardan 5-i isə 1×15×5 formasını təşkil edə bilər. Bu iki forma 1×15×8 kuboidinin yaradılmasında istifadə oluna bilər. Onlardan ikisi 2×15×8 kuboidi əmələ gətirə bilər. Müzakirə etdiyimiz əməliyyatlardan daha sıx istifadə edə bilərik: (1, 3, 5) → (1, 3 + 5, LCM(3,5)) = (1, 8, 15) → (2, 8, 15) → (2, 15, 8).
Hər dəfə 1×3×5 parçaları birləşdirildikdə, kubların ümumi sayı 5-in çoxluğudur. 3 × 9 × 14 5 ilə parçalanmadığı üçün 3×9×14 kuboidi 1×3×5 ölçüsündə olan parçalardan yaratmaq mümkün deyil.
 Harmonik və qeyri-harmonik parçalar üçün qaydaların məcmusu
Harmonik və qeyri-harmonik parçalar üçün qaydaların məcmusu
Öyrəndiklərimiz haqqında ümumi məlumat:
- Əgər bir kuboidin uzunluğu bir parçanın uzunluqlarının çoxluğudursa, onda parçanın harmonik olmasından asılı olmayaraq, həmin parçanın nüsxələrindən əmələ gələ bilər. Belə kuboidlər eyni oriyentasiyada bütün parçalarla əmələ gələ bilər, lakin parçaların müxtəlif oriyentasiyalara malik olduğu tədbirlər də mövcud ola bilər.
- Əgər parça harmonikdirsə, onda əmələ gələn hər hansı bir kuboid parçanın uzunluqlarının çoxluğu olan uzunluqlara malik olmalıdır. Nəticədə harmonik parçalardan əmələ gələn hər hansı bir kuboid eyni oriyentirdə bütün parçalara malik ola bilər, halbuki bu həmişə lazım deyil.
- Əgər parça harmonik deyilsə, bəzi kuboidlər əmələ gələ bilər ki, onların uzunluğu parçanın uzunluqlarının çoxluğu deyil (bax: üçüncü və dördüncü əməliyyatlar). Bu halda parçaların hamısı eyni oriyentasiyaya malik ola bilməz . Qeyri-harmonik parçalardan istifadə etməklə, daha əvvəl təsvir olunan 4 üsuldan istifadə etməklə müxtəlif formalı kuboidlər yaratmaq olar.
 Bu müşahidələr yalnız üç ölçüdə keçərlidirmi?
Bu müşahidələr yalnız üç ölçüdə keçərlidirmi?
XEYR. Bu kontekstdə 3 ölçü ilə bağlı xüsusi bir şey yoxdur. Əslində uzunluqlardan birini 1-ə bərabər təyin etmək problemin 2 ölçüyə endirilməsinə bərabərdir. Nəticələr 3-dən çox ölçüdə də keçərlidir. Məsələn, 1×3×12×24 parçası harmonikdir. Buna görə də, bu 4-ölçülü parçalardan əmələ gələn hər hansı 4 ölçülü kuboid A, B × 3, C × 12 və D × 24 ölçülərinə malik olmalıdır. Bəzi müsbət integerlər üçün A, B, C və D.
 Əl-ələ tapmacaları necə əldə etmək olar?
Əl-ələ tapmacaları necə əldə etmək olar?
4 ölçülü parçaları necə düzəltmək lazım olduğunu deyə bilmərik :) ancaq 3 ölçüdə bir çox ehtiyyat zarı varsa, parçaları meydana gətirmək üçün onları birlikdə lentə ala bilərsiniz.
Məsələn, 5×5×5 qutusu əvəzinə ayaqqabı qutusu istifadə etmək olar. Əgər biri onu diaqonal olaraq tutarsa, parçalar yerləşdirildiyi yerdə qalar.
Tapmacaların bəzilərinin hündürlüyü 1 -dir (məsələn, "1×7×10 1") və buna görə də 2-ölçülü tapmacalardır. Bu tapmacalar üçün parça kimi istifadə etmək üçün qrafik kağızdan düzbucaqlıları kəsmək olar.
 Etiraf
Etiraf
"5x5x5 1" adlı tapmacanın taxta versiyasını riyaziyyat sərgisində görərkən tapmacaların yığılmasına marağımız alovlandı. Müəllifi məşhur riyaziyyatçı Con Horton Konveyə istinad edildikdən sonra ondan "3x3x3 2", "5x5x5 2", "5x5x5 3" tapmacalarına rast gəldik.
"Yalnız bir növ parça ilə yığılma" bölməsi hollandiyalı riyaziyyatçı de Bruijnin fəaliyyətindən ilham almışdır. De Bruijnin düzbucaqlı parçaların yığılması ilə bağlı müşahidələri haqqında ətraflı məlumat almaq üçün bu məqaləyə müraciət edin. De Bruijnin harmonik parçaların xüsusiyyətlərini sübut edən dəlilini buradan oxuya bilərsiniz.





Yeniliklər üçün izləyin və ya abunə olun: