Упаковка©
У цій головоломці перемогли/зіграли: 16060/24480
Чому я маю прочитати цю «Їжу для роздумів»?
Тому що ви будете здивовані.
Спробувавши кілька пазлів, яка область математики, на вашу думку, є найкориснішою для їх вирішення:
1) Алгебра, 2) Теорія ймовірностей, 3) Геометрія, 4) Теорія чисел, 5) Симетрії, 6) Інша область?
Найкориснішим виявляється подумати про подільність чисел, особливо про подільність на 2. Це предмет теорії чисел. Речі, які ми складаємо, є геометричними об'єктами, але це не означає, що для вирішення головоломок потрібні геометричні знання. З геометрії нам потрібно знати, що таке площа квадрата або прямокутника, але не більше того.
Для деяких головоломок роздуми про симетрію також дуже корисні.
Швидкі підказки
Це підказки для тих, хто звертається за допомогою, але не цікавиться математичним підґрунтям.
- Дивлячись на цифри поруч із «Ця головоломка виграла/зіграна» для кожної головоломки, перевірте, які з них найпростіші. Починати з найпростіших головоломок завжди гарна ідея, і це дасть вам практику в поводженні з інтерфейсом.
- Головоломки «2×3×3 1» і «2×3×3 2» легко вирішуються методом проб і помилок.
- Якщо ваша перша спроба головоломки "1×7×10 1" не увінчалася успіхом, поверніть шматочки під час наступної спроби.
- "1×7×7 1" - це головоломка, в якій допомагають роздуми про симетрію. Причина в тому, що ємність (сітка) має квадратну основу з 4 однаково довгими сторонами, і ми маємо 4 довгих шматка однакової форми. Тому розташовувати їх слід симетрично. Є лише одна фіолетова деталь квадратної форми. Щоб мати обертально симетричний розчин на 90°, цей шматок повинен бути посередині. У будь-якому іншому місці порушиться симетрія розчину під кутом 90°.
- Головоломки з темнішими кнопками вимагають більше роздумів. Почніть з повного розуміння головоломки "3×3×3 2", перш ніж перейти до 5×5×5.
Як можна вирішувати ці головоломки без проб і помилок?
Ось кілька підказок:
- Розбийте складну проблему на легші, тобто на підцілі. Наприклад, щоб заповнити всю ємність, потрібно заповнювати кожен шар.
- Розташовуйте шматочки симетрично, особливо якщо контейнер симетричний, як куб 3×3×3 або контейнер квадратної форми 1×7×7.
- Використовуйте надану інформацію по максимуму. Які бувають розміри шматків? Скільки з них мають однакову форму?
Решта цієї «Їжі для роздумів» має на меті вирішити всі головоломки без спроб і помилок, замість цього придумуючи прості питання і відповідаючи на них.
Визначення
Для наочності наведемо кілька термінів, які ми будемо використовувати для обговорення проблем з упаковкою:
Шматок
Одна з фігур, які будуть з'єднані разом, щоб утворити більшу тверду речовину.
Непарний шматок — це шматок, довжина якого всі непарні, наприклад, шматок 1×1×1 або шматок 1×3×5.
Шматок є парним, якщо він має принаймні дві рівні довжини, наприклад 1×2×4 або 2×2×2.
Чи всі фігури парні чи непарні?
НІ. Шматок з рівно однією рівною довжиною, наприклад 1×2×3, не підходить під жодне з визначень. У наступних розділах ми зосередимося на непарних і непарних фігурах.
Кубоїд/контейнер
Кубоїд – це прямокутна призма. Ми використовуємо слово «контейнер» для позначення порожньої оболонки кубовида. Під «кубоїдом» ми говоримо вміст контейнера. Ємність наповнюється шматками, а з шматочків створюється кубоїд.
Шар
Пласт - це зріз товщиною 1 в напрямку, паралельному лицьовій стороні ємності. Контейнер 3×4×5 має 3 шари розміром 4×5, 4 шари розміром 3×5 і 5 шарів розміром 3×4.
Скільки шарів має контейнер 1×5×7?
Він має один шар 5×7, п'ять шарів 1×7 і сім шарів 1×5. Всього в ньому 1 + 5 + 7 = 13 шарів.
Куб
Точніше, куб 1×1×1, а не більший куб. Фігура 1×1×1 складається з 1 кубика, тоді як фігура 1×1×3 складається з 1 × 1 × 3 = 3 кубиків.
Будівельний блок
Кілька частин, прикріплених один до одного, утворюють будівельний блок. Цікаві будівельні блоки матимуть симетрію. Для складніших головоломок контейнер заповнять кілька однакових або дзеркально ідентичних будівельних блоків плюс центральна частина.
Стратегія
Половина розв'язання складної задачі полягає в тому, щоб розбити складну проблему на більш дрібні проблеми.
Для цього слід задавати собі прості питання. Наступні питання будуть корисні при вирішенні пазлів з упаковки.
Чи можна кожен кубоїд утворити з шматочків розміром 1×2×2 ? Наприклад, чи можна сформувати кубоїд 3×3×3, використовуючи лише відрізки розміром 1×2×2 ?
НІ. Фігура 1×2×2 складається з парної кількості кубиків. Отже, будь-яка кількість штук 1×2×2 разом матиме парну загальну кількість кубиків. Оскільки кубоїд 3×3×3 складається з непарної кількості кубиків, його не можна сформувати таким чином.
У наступних кількох розділах ми розглянемо, як подільність, особливо на 2, визначає, як потрібно розміщувати шматочки для вирішення певних головоломок.
Чи може 1×2×2 штуки принаймні заповнити будь-який шар контейнера 3×3×3?
Відповідь знову – НІ. Площа в шарі, яка може бути зайнята шматком, - це площа однієї з граней шматка, чи не так?
Які грані фігури 1×2×2?
Деталь 1×2×2 має дві пари паралельних граней 1×2 і одну пару 2×2 граней.
Що є областями цих облич і що спільного між цими ділянками?
Площі дорівнюють 1 × 2 = 2 і 2 × 2 = 4. 2 і 4 є парними числами.
Ми спостерігаємо, що шматок 1×2×2 може займати лише парну кількість кубиків (2 або 4) у кожному шарі.
Чи справедливо це для всіх парних шматків?
Кожна грань виробу має дві довжини. Так як парні фігури мають не більше однієї непарної довжини, то кожна їх грань буде мати хоча б одну парну довжину. Оскільки парне × непарне = парне, площа кожної грані буде парною. Ось чому ми називаємо їх парними шматочками!
Ми дізналися, що кубоїди з непарною довжиною сторін не можуть бути утворені тільки з парних шматків. Шар з непарною площею теж не можна заповнювати парними шматками. Тому пазл "3×3×3 2" має кілька 1×1×1 частин, які є непарними частинами.
Ось ще одне корисне питання, яке слід розглянути:
Чи є один з двох типів фігур (1×1×1 і 1×2×2) більш «цінним», ніж інший?
ТАК. Якби у нас було всього 1×1×1 шматочк, то будь-яка головоломка була б банальною, погодьтеся? Якби у нас було всього 1×2×2 штуки, то непарний контейнер не можна було б заповнити, як показано вище.
Очевидне питання: яка мінімальна кількість штук 1×1×1, яка може заповнити контейнер 3×3×3?
Природно, що виникають такі питання:
Чому достатньо трьох штук по 1×1×1?
Щоб відповісти на це питання, ми порівняємо кількість непарних шарів (шарів з непарною площею) з кількістю шарів непарної площі, які можна заповнити парними шматочками і тільки 3 кубиками.
Скільки шарів має контейнер 3×3×3?
У кожному з трьох напрямків (ширина, висота, глибина) контейнер має 3 шари. Є 3 + 3 + 3 = 9 непарних шарів, які заповнюються при заповненні контейнера.
Скільки непарних шарів 3×3 можна завершити однією фігурою 1×1×1 (а деякі навіть 1×2×2)?
Три шари: горизонтальний шар і два вертикальні шари, які містять шматок 1×1×1. Тому 3 кубики можуть допомогти заповнити максимум 3 & рази 3 = 9 шарів.
Це показує, що необхідно 3 кубики, а оскільки головоломка "3×3×2 2" вирішувана, 3 кубиків також достатньо, щоб заповнити 9 непарних шарів.
Що це говорить нам про розташування 3 кубиків у
Пазл "3×3×3 2"?
У кожному з 9 шарів може бути тільки 1 кубик, а не 0 кубиків і не 2 кубики! В іншому випадку 3 кубиків буде недостатньо для 9 шарів.
Це і є прорив для рішення. Крім того, єдиний спосіб розміщення кубиків - по діагоналі - при цьому один кубик знаходиться в центрі, а два інших кубика - по діагоналі протилежних кутах. В іншому випадку громіздкі 1×2×2 шматочки будуть занадто великими, щоб заповнити простір навколо 3 кубиків.
Тому покладіть один кубик у кут, а три штуки 1&2×2 симетрично навколо цього куба. Покладіть один кубик в центр, один в протилежний кут, а решта будуть очевидні.
Чого ще ми можемо навчитися з цього рішення? Наприклад, чи має він симетрії?
Симетрії видно після розміщення першого куба в кутку і трьох фігур 1×2×2 навколо нього. Розв'язок має обертальну симетрію на 120° з діагоналлю куба як віссю обертання (120° = 1/3 від повного обертання кола).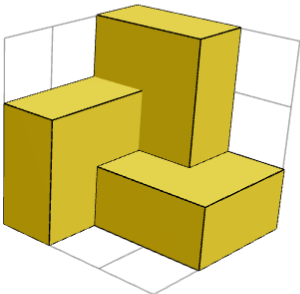
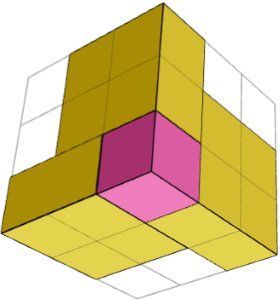
Чи є розв'язок сумою однакових або симетричних будівельних блоків, кожен з яких складається з кількох частин?
ТАК. Кубоїд - це сума 2 будівельних блоків, які дзеркально симетричні (1 куб у кутку + три фігури 1×2×2 навколо нього) і одного куба посередині. На наведених вище 2 зображеннях показаний один будівельний блок з 2-х сторін.
Чи є інший спосіб вирішити цю головоломку, використовуючи різні будівельні блоки?
ТАК. На лівому та правому зображеннях нижче показані два дзеркальні симетричні будівельні блоки для головоломки "3×3×3 2". Їх можна поєднати з центральним кубом (середнім зображенням) для вирішення головоломки.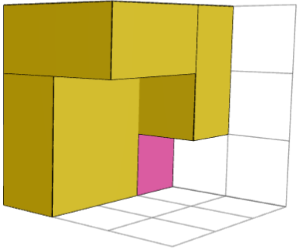
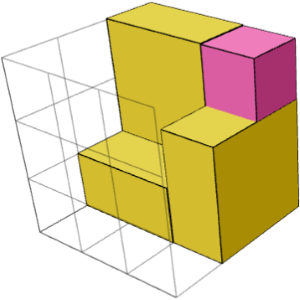
Чому ми повинні думати про будівельні блоки?
Простіше використовувати невелику задану кількість штук і створити з них щось симетричне, ніж заповнювати більшу ємність всіма шматочками.
Чи можна використовувати будівельні блоки для вирішення більших головоломок, таких як "3×5×7 1"?
ТАК. Більші контейнери, навіть якщо їх довжина різна, можна наповнити за допомогою ідентичних/дзеркально симетричних будівельних блоків. Існує кілька способів вирішення головоломки «3×5×7 1» з використанням будівельних блоків і центральної непарної частини. Ми залишаємо вам знайти кілька прикладів.
Як ми знаємо, з яких частин має складатися будівельний матеріал?
Давайте спочатку подумаємо про центр непарного кубоіда. Оскільки центральне положення унікальне, якщо ми хочемо симетричного рішення, центр повинен займати шматок з такою ж формою, як і контейнер. Кубоїд 3×3×3 є кубом, тому центральною фігурою для цього має бути куб. Шматок 1×2×2 у центрі порушить симетрію.
Це означає, що у нас є 6 жовтих і 3 − 1 = 2 рожеві шматочки для побудови кількості однакових будівельних блоків.
Скільки будівельних блоків ми повинні спробувати створити?
Будівельні блоки повинні утворювати кубоїд за вирахуванням центральної частини. Таким чином, кількість жовтих частин у будівельному блоці має бути дільником 6 (загальна кількість жовтих блоків), а кількість рожевих частин будівельного блоку має ділитися на 2 (кількість рожевих кубиків, що залишаються після резервування одного для центру).
Таким чином, число N однакових будівельних блоків є найбільшим спільним дільником числа однакових частин, тут 6 і 2, що дорівнює НСД(6,2) = 2. Отже, ми повинні створити будівельний блок з 2 / 2 = 1 рожевого кубика і 6 / 2 = 3 жовтих блоків. Що ми і зробили.
Узагальніть математичний алгоритм, щоб використовувати його для великих головоломок.
Для непарної ємності:
- Вирівняйте непарні шматки, щоб переконатися, що вони не перекриваються в жодному шарі. Вони повинні з'єднувати один кут ємності з протилежним кутом ємності. Якщо непарні фігури є кубиками, вони утворюють діагональ. Якщо непарні фігури більші (1х1х3), то вони утворюють не пряму діагональ.
- Якщо є тільки один вид рівного шматка, то використовуйте їх для наповнення ємності.
- Якщо є різні види парних штук:
- Відкладіть в сторону центральну непарну частину. З решти фігур знайдіть найбільший спільний дільник N чисел штук різних типів. N – кількість будівельних блоків.
- Створіть N однакових будівельних блоків і з'єднайте їх разом з центральною частиною у випадку непарного контейнера.
У той час як невеликі головоломки можна легко вирішити методом проб і помилок, ця стратегія не працює для великих головоломок. Наше дослідження непарних і непарних фігур виявляє важливу причину: розміщення непарних фігур має вирішальне значення, оскільки існує дуже мало способів їх правильного розміщення. Використовуючи метод проб і помилок, можна зробити помилку прямо на старті і зрозуміти, що щось пішло не так, тільки після того, як поставив багато фігур. Це неймовірно ускладнює визначення того, що спричинило помилку, тому немає корисного зворотного зв'язку; Метод проб і помилок не ефективний для великих контейнерів. Потрібне мислення.
Упаковка тільки з одним типом полотна
У цьому розділі ми розглянемо розміри кубоїдів, які можуть бути утворені з одного типу шматка. Це теоретичний розділ, не потрібний для вирішення перерахованих вище головоломок. Цей розділ не вимагає складної математики.
Маючи достатню кількість 1×1×1 штук, ми можемо легко сформувати кубоїд будь-якого розміру. Але як щодо інших штук, таких як 2×3×4 або 1×2×5 штук? Є два основних питання, які потрібно дослідити. По-перше, враховуючи довжини шматка та довжини кубоіда, як ми можемо визначити, чи можна створити кубоїд з копій шматка? По-друге, як ми, починаючи з однієї частини, можемо створити довжини кубоіда, який можна утворити? У цьому розділі ми розглянемо простіші запитання, досліджуючи ці дві важливі проблеми.
Чи можна утворити кубоїд 2×6×10 лише з 1×2×5 штук?
ТАК! Три штуки 1×2×5 можна розмістити поруч, щоб утворилася форма 1×6×5 (3 × 2 = 6). Потім ми можемо створити другу фігуру 1×6×5 і об'єднати їх у форму 1×6×10. Нарешті, дві фігури 1×6×10 можна розмістити разом, щоб утворити кубоїд 2×6×10.
Чи можна сформувати кубоїд 10×12×14, використовуючи лише шматочки розміру 2×5×6 ?
Підказка
Не обов'язково уявляти, як будуть розташовуватися твори.
Ще одна підказка?
Шматок 2×5×6 такий самий, як 5×6×2, оскільки його можна обертати.
Відповідь
ТАК. Оскільки 10 / 5 = 2, 12 / 6 = 2 і 14 / 2 = 7, більший кубоїд можна розглядати як розташування 2×2×7 частин 5×6×2. 5×6×2 штуки можна розміщувати з однаковою орієнтацією.
Як можна узагальнити ці результати?
Припустимо, у нас є тільки шматки розміром x × y × z. Тоді побудова кубоїда X & разів Y & Z можлива, якщо існують додатні цілі числа A, B, C такі, що Ax, By і Cz дорівнюють X, Y і Z в деякому порядку.
Скільки штук буде використано в даному випадку?
Ми можемо розташовувати фігури А в одному напрямку, В - в іншому, а С - в третьому. Всього будуть використані фігури A × B & times C .
Чому Ax, By і Cz можуть дорівнювати X, Y і Z в будь-якому порядку?
Контейнер розміром X × Y × Z дорівнює кубоїду Z × X & Y . Порядок довжин не має значення, тому що кубоїд можна обертати.
Чи вірно, що будь-який кубоїд, утворений з 1×2×3, повинен мати довжини A, B × 2, C × 3, для деяких натуральних чисел A, B, C ?
НІ. Якщо всі фігури 1×2×3 орієнтовані в одному напрямку, то кубоїд матиме розмір A × (B × 2) × (C × 3). Але фігури можуть бути орієнтовані по-різному і все одно утворювати кубоїд. Наприклад, частини 1×2×3 можуть утворювати кубоїд 1×5×6, навіть якщо 1, 5 і 6 не дорівнюють A, B × 2 і C × 3 у будь-якому порядку. Іншим прикладом є головоломка "1×7×10 1", яка складається з 1×2×5 частин.
Який зв'язок між довжинами шматка і довжинами кубоїда в цих двох прикладах?
В обох цих прикладах одна з довжин кубоїда є сумою двох довжин шматка. Інша довжина кубоїда - це LCM (найменше спільне кратне) тих самих двох довжин фігури. У випадку кубоїда 1×5×6, утвореного з 1×2×3 штук, ми маємо 1×5×6 = 1 × (2 + 3) × LCM(2,3). Аналогічно, 1×7×10 = 1 × (2 + 5) × LCM(2,5).
Як ми можемо використовувати цей факт, щоб знайти спосіб генерації довжин кубоїдів, які можуть бути побудовані з даного шматка?
Ми починаємо з представлення довжини шматка у вигляді впорядкованої трійки. Наприклад, фігура 1×2×3 представлена (1, 2, 3). Тепер є 3 операції, які ми можемо кілька разів виконувати, щоб дати довжини кубоїдів, які можна сформувати з цього шматка. Вони бувають:
- Змініть порядок довжин. Це відомо як перестановка. У нашому випадку він являє собою обертання в 3-вимірному просторі. Як приклад можна навести
(1, 2, 3) → (2, 3, 1). - Помножте довжини на натуральні числа A, B і C відповідно. Це відповідає формуванню більшого кубоїда шляхом розміщення частин A в одному напрямку, B — в іншому, а C — у третьому напрямку. Наприклад, ми можемо помножити на 1, 4 і 3, щоб отримати (1, 2, 3) → (1 &помножити на 1, 4 &помножити на 2, 3 &помножити на 3) = (1, 8, 9).
- Візьміть дві довжини і замініть одну їх сумою, а іншу - їх LCM.. Це відповідає утворенню більшого кубоїда з фігурами, орієнтованими в різні сторони. Наприклад, вибравши довжини 2 і 3, ми отримаємо (1, 2, 3) → (1, 2 + 3, LCM(2,3)) = (1, 5, 6).
Чи можна об'єднати частини4-м способом, щоб отримати кубоїд, форма якого відрізняється від результату3-ї операції?
ТАК. Розглянемо шматок розміром x × y × z. Третя операція дає кубоїд розміром x × (y + z) × LCM(y,z), де одна довжина x є незмінною від шматка до кубовида.
Аналогічним, але іншим способом було б знову поставити LCM(y,z)/y багато штук поруч один з одним, а LCM(y,z)/y багато штук поруч, як і раніше, але тепер повернути один набір на 90° так, щоб два блоки мали однакову довжину LCM(y,z), але різну висоту. Говорячи математичними термінами, ми не приєднуємо x × y × LCM(y,z) та x × z × LCM(y,z) для утворення x × (y + z) × LCM(y,z). Замість цього, один з них, скажімо, x × z × LCM(y,z), повертається в z × x × LCM(y,z) і потім приєднується.
Тоді площа прямокутної основи не (y + z) × LCM(y,z), а скоріше (x + z) × LCM(y,z). Тоді два будівельні блоки x × y × LCM(y,z) і z × x × LCM(y,z) мають довжини x і z, відповідно, в X-напрямку.
При складанні LCM(x,z)/x багато будівельних блоків висотою x і LCM(x,z)/z багато будівельних блоків висоти z, обидва стеки досягають висоти LCM(x,z). Коли вони приєднуються, результатом є кубоїд розміром LCM(x,z) × (x + z) × LCM(y,z), який має іншу форму та розмір, ніж будь-який кубоїд, отриманий в результаті третьої операції.
Можна повторювати ці операції в будь-якому порядку, спочатку генеруючи кубоїд з шматка, а потім використовуючи кубоїд як «шматок» для створення ще більшого кубою. Раніше ми обговорювали, як кубоїд 2×6×10 може бути утворений з 1×2×5 штук. У цьому випадку потрібна тільки одна операція, помноження на 2, 3 і 2 відповідно: (1, 2, 5) → (2 &помножити на 1, 3 & 2, 2 &помножити на 5) = (2, 5, 10).
Таким чином, фігури розміру x × y × z можуть не тільки будувати кубоїди розміром Ax × By × Cz, але, наприклад, також з розміром x × (y + z) × LCM(y,z), де LCM(y,z) є найменшим спільним кратним y та z. Складаючи кілька цих будівельних блоків разом, ми отримуємо кубоїди розміром Ax × B(y + z) + C(LCM(y,z)).
Зараз ми розглянемо особливий вид шматка. Твір є гармонійним , якщо кожна з його більших довжин ділиться на наступну меншу довжину. Наприклад, твір 1×2×6 є гармонійним, оскільки 2 / 1 = 1 і 6 / 2 = 3. Фігура 1×4×6 не є гармонічною, оскільки 6 не кратна 4.
Чи є гармоніка 1×2×3?
НІ, тому що 3 не ділиться на 2.
Що робить гармонійні твори особливими в упаковці? Як вони співвідносяться з нашим обговоренням довжин штук і кубоїдів?
Ми вже спостерігали, що будь-яка частина може утворювати кубоїд, довжини якого кратні довжині шматка. Виявляється, що довжини будь-якого кубоіда, утвореного однаковими гармонійними фігурами, повинні бути кратні довжині фігур. Тобто, якщо гармонійний твір має довжини x, y і z, будь-який кубоїд, утворений з копій цього шматка, повинен мати одну довжину, що ділиться на x, іншу ділиться на y, а третю ділиться на z. Хоча це просте твердження, доказ вимагає концепцій, що виходять за рамки цього веб-сайту. Посилання на доказ можна знайти в розділі «Подяка».
Як цей факт узгоджується з чотирма операціями, про які ми розповіли вище?
Ми можемо почати з розгляду твору як також кубовида, утвореного з однієї копії шматка. Шматок x × y × z також є кубоїдом x × y × z . Довжини цього кубоїда кратні довжині шматка, оскільки кожне число кратне самому собі. Ми покажемо, чому чотири методи, які ми запровадили, дають кубоїди, довжини яких все ще кратні довжині шматка.
- Зміна порядку довжин (перестановка): це просто обертання, і насправді не змінює довжини кубовида. Довжини кубоїда все одно будуть кратні довжині шматка.
- Множення довжин кубоїда на натуральні числа: якщо довжини кубоїда вже кратні довжині шматка, це не зміниться. Вони просто стануть більшими кратними. Якщо X = Ax кратний x, то DX = DAx також кратний x, для будь-якого натурального числа D.
- Заміна двох довжин на їх суму і ЛКМ: ось чому важливі гармонійні п'єси; Нам потрібно буде скористатися визначенням гармонійних творів. Припустимо, ми почали з гармонійної фігури (x, y, z), з якої ми вже утворили кубоїд (Ax, By, Cz). Порядок довжин не має значення, так як кубоїд можна обертати. Тепер ми виконаємо третю операцію на будь-яких двох довжинах кубовида, скажімо, Ax і By: (Ax, By, Cz) → (Ax + By, LCM(Ax, By), Cz). Тепер, оскільки твір (x, y, z) є гармонійним, одна з двох довжин x і y кратна іншій. Припустимо, y кратне x. Отже, By також кратна x, а оскільки Ax також, сума Ax + By кратна x. Далі, LCM(Ax,By) є найменшим спільним кратним Ax і By, тому воно за визначенням кратне By, отже, воно ділиться на y. Нарешті, Cz - це, звичайно ж, кратне z. Таким чином, довжини нового кубоїда (Ax + By, LCM(Ax, By), Cz) все ще кратні довжині фігури.
- А як щодо четвертої операції? Оскільки ця операція схожа на третю операцію, аргумент, представлений вище, може бути адаптований для цього випадку. Ми залишаємо це як вправу.
Ми показали, що чотири операції, виконані багаторазово в будь-якому порядку над будь-якою гармонійною п'єсою, призведуть до отримання кубоіда, довжини якого кратні довжині фігури. Важливо відзначити, що в нашому обговоренні третьої операції (і четвертої!) ми спираємося на те, що твір є гармонійним. Коли твір не є гармонійним, аргумент не спрацьовує. У цьому полягає ключова відмінність між гармонійними та негармонічними творами. Для гармонійних п'єс третій і четвертий методи не дають зайвих форм у порівнянні з першими двома методами.
В результаті будь-який кубоїд, утворений з гармонійних фігур, може мати всі фігури в однаковій орієнтації. Тому, якщо ми намагаємося сформувати кубоїд з однакових гармонійних фігур, досить спробувати розташувати їх всі обличчям в одному напрямку. Якщо такої можливості немає, то кубоїд взагалі не може бути сформований.
Оскільки фігура 1×2×2 є гармонійною, будь-який кубоїд, утворений з копій цього шматка, повинен мати довжини A, B × 2 і C × 2 для деяких цілих чисел A, B і C. На зображенні нижче показаний кубоїд 5×4×4, утворений 1×2×2 частинами, які всі мають однакову орієнтацію.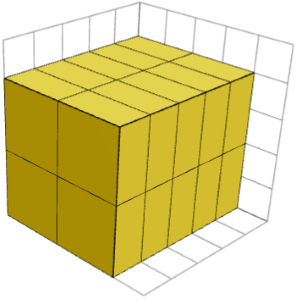
Які значення А, В і С ?
Встановивши A, B × 2 і C × 2 рівними 5, 4 і 4 відповідно, ми знайдемо A = 5 / 1 = 1, B = 4 / 2 = 2, а C = 4 / 2 = 2.
При упаковці з гармонійними фігурами, чи повинні деталі бути спрямовані в одному напрямку?
НІ! Хоча завжди можливо, щоб усі частини мали однакову орієнтацію, можуть бути й інші розташування, але вони не утворюють нових форм. На зображенні нижче показаний інший спосіб формування кубоїда 5×4×4 з 1×2×2 штук.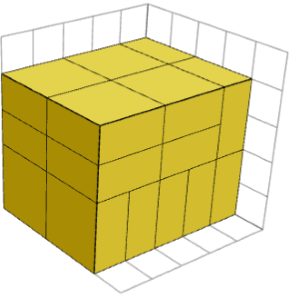
Які правила для негармонічних творів?
При роботі з негармонійною фігурою x × y × z можна утворити деякі кубоїди, розміри яких не Ax × By × Cz для будь-яких цілих чисел A, B, C. Наприклад, кубоїд 1×5×6 можна створити з 1×2×3 штук. Це результат третьої операції, про що говорилося раніше.
Важливо відзначити, що кількість кубиків в кубоїді завжди повинна ділитися на кількість кубиків в штуці. Коли довжини куба не кратні різній довжині шматка, одна з довжин кубоїда буде спільним кратним принаймні 2 довжин фігури, завдяки третьому і четвертому методам. Цей факт може бути використаний для визначення того, чи можуть бути утворені певні кубоїди з негармонійних фігур.
Деякі питання для повторення того, що ми розглянули:
Чи може 2×4×12 штук утворити кубоїд розміром 4×8×36 ? А як щодо кубоїда розміром 10×10×12 ?
Так як 4 / 2 = 2, 8 / 4 = 2, а 36 / 12 = 3, то можна утворити кубоїд розміром 4×8×36.
Одна з довжин кубоїда 10&10×12 ділиться на 12. Іншими довжинами є 10 і 10, жодна з яких не ділиться на 4. Отже, довжини кубоїда 10×10×12 не кратні довжині шматка. Оскільки 12 / 4 = 3 і 4 / 2 = 2, шматок гармонійний, отже, кубоїд 10×10×12 не може бути утворений з шматочків розміром 2×4×12.
Чи можуть шматочки розміром 1×3×5 утворити кубоїд розміром 2×15×8 ? А як щодо кубоїда 3×9×14?
Оскільки 5 не ділиться на 3, твір не є гармонійним. Ми не можемо застосувати свої знання про гармонійні твори.
З цими шматочками можна сформувати кубоїд розміром 2×15×8. Три шматочки 1×3×5 можуть утворювати форму 1×3×15 (або 1×15×3), а 5 частин, розташованих по-різному, можуть утворювати форму 1×15×5. Ці дві фігури можуть бути використані для створення кубоїда 1×15×8, дві з яких можуть утворити кубоїд 2×15×8. Ми можемо використовувати розглянуті нами операції для більш стислого викладу: (1, 3, 5) → (1, 3 + 5, LCM(3,5)) = (1, 8, 15) → (2, 8, 15) → (2, 15, 8).
Щоразу, коли об'єднуються 1×3×5 штук, загальна кількість кубиків кратна 5. Оскільки 3 × 9 × 14 не ділиться на 5, кубоїд 3×9×14 не може бути створений з шматочків розміром 1×3×5.
Короткий зміст правил для гармонічних і негармонічних творів
Ось огляд того, що ми дізналися:
- Якщо довжини кубоїда кратні довжині шматка, то він може бути утворений з копій цього шматка, незалежно від того, чи є твір гармонійним. Такі кубоїди можуть бути сформовані з усіма фігурами в одній орієнтації, але також можуть існувати схеми, в яких фігури мають різну орієнтацію.
- Якщо фігура є гармонійною, то будь-який утворений кубоїд повинен мати довжини, кратні довжині фігури. В результаті, будь-який кубоїд, утворений з гармонійних фігур, може мати всі фігури в однаковій орієнтації, хоча це не завжди необхідно.
- Якщо фігура не є гармонійною, то можуть утворитися деякі кубоїди, довжини яких не кратні довжині шматка (див. третю і четверту операції). При цьому всі фігури не можуть мати однакову орієнтацію. Використовуючи негармонійні фігури, можна створювати кубоїди різної форми, використовуючи 4 способи, описані раніше.
Чи справедливі ці спостереження лише в трьох вимірах?
НІ. У цьому контексті нічого особливого в 3 вимірах немає. Фактично, встановлення однієї з довжин рівною 1 еквівалентно зменшенню задачі до 2 вимірів. Результати також дійсні в більш ніж 3 вимірах. Наприклад, твір 1×3×12×24 є гармонійним. Отже, будь-який 4-вимірний кубоїд, утворений з цих 4-вимірних частин, повинен мати розміри A, B & times 3, C × 12 і D & 24 для деяких натуральних чисел A, B, C і D.
Як отримати практичні головоломки?
Ми не можемо розповісти, як зробити 4-мірні деталі :) Але в 3-вимірних розмірах, якщо у вас багато запасних кубиків, ви можете скріпити їх скотчем, щоб сформувати фігури.
Замість коробки 5×5×5 можна використовувати, наприклад, коробку з-під взуття. Якщо тримати її по діагоналі, фігури залишаться там, де вони розміщені.
Деякі з головоломок мають висоту 1 (наприклад, "1×7×10 1") і тому є 2-вимірними головоломками. Можна вирізати прямокутники з міліметрового паперу, щоб використовувати їх як шматочки для цих головоломок.
Визнання
Наш інтерес до пакування пазлів спалахнув, коли ми побачили дерев'яну версію головоломки «5х5х5 1» на математичній виставці. Слідуючи за посиланням на її автора, відомого математика Джона Хортона Конвея, ми знайшли у нього головоломки «3х3х3 2», «5х5х5 2», «5х5х5 3».
Розділ «Упаковка лише з одним типом деталей» був натхненний роботами голландського математика де Брюйна. Щоб дізнатися більше про спостереження де Брюйна щодо пакування прямокутних деталей, зверніться до цієї статті. Доказ властивостей гармонічних творів де Брюйна можна прочитати тут.
Слідкуйте за оновленнями або підписуйтесь на них: