ការវេចខ្ចប់©
ល្បែងផ្គុំរូបនេះបានឈ្នះ/លេង៖ 15609/23779
ហេតុអ្វីបានជាខ្ញុំគួរអាន "Food for Thought" នេះ?
ព្រោះអ្នកនឹងភ្ញាក់ផ្អើល។
បន្ទាប់ពីព្យាយាមល្បែងផ្គុំរូបវេចខ្ចប់មួយចំនួន តើអ្នកគិតថាផ្នែកគណិតវិទ្យាមួយណាមានប្រយោជន៍បំផុតសម្រាប់ការដោះស្រាយពួកវា៖
1) ពិជគណិត, 2) ទ្រឹស្តីប្រូបាប៊ីលីតេ, 3) ធរណីមាត្រ, 4) ទ្រឹស្តីលេខ, 5) ស៊ីមេទ្រី, 6) តំបន់ផ្សេងទៀត?
អ្វីដែលប្រែទៅជាមានប្រយោជន៍បំផុតគឺគិតអំពីការបែងចែកលេខ ជាពិសេសការបែងចែកដោយ 2. នេះគឺជាប្រធានបទនៃទ្រឹស្តីលេខ។ អ្វីដែលយើងជង់គឺជាវត្ថុធរណីមាត្រ, but that doesn't mean that geometric knowledge is needed to solve the puzzles. ពី Geometry យើងត្រូវដឹងថាផ្ទៃនៃការ៉េ ឬចតុកោណកែងគឺជាអ្វី ប៉ុន្តែគ្មានអ្វីបន្ថែមទៀតទេ។
សម្រាប់ល្បែងផ្គុំរូបមួយចំនួន ការគិតអំពីស៊ីមេទ្រីក៏មានប្រយោជន៍ផងដែរ។
ការណែនាំរហ័ស
ទាំងនេះគឺជាការណែនាំសម្រាប់អ្នកដែលកំពុងស្វែងរកជំនួយ ប៉ុន្តែមិនចាប់អារម្មណ៍លើផ្ទៃខាងក្រោយគណិតវិទ្យា។
- ដោយមើលលេខនៅជាប់នឹង "This puzzle won/played" សម្រាប់រូបផ្គុំនីមួយៗ ពិនិត្យមើលថាតើមួយណាងាយស្រួលបំផុត។ ការចាប់ផ្តើមជាមួយនឹងល្បែងផ្គុំរូបដែលងាយស្រួលបំផុតគឺតែងតែជាគំនិតល្អ, and will give you practice with handling the interface.
- ល្បែងផ្គុំរូប "2×3×3 1" និង "2×3×3 2" ត្រូវបានដោះស្រាយយ៉ាងងាយស្រួលដោយការសាកល្បងនិងកំហុស។
- ប្រសិនបើការព្យាយាមលើកដំបូងរបស់អ្នកលើរូបផ្គុំ "1×7×10 1" មិនទទួលបានជោគជ័យ សូមបង្វិលបំណែកនៅលើការព្យាយាមបន្ទាប់របស់អ្នក។
- "1×7×7 1" គឺជាល្បែងផ្គុំរូបដែលការគិតអំពីស៊ីមេទ្រីជួយ។ ហេតុផលគឺថាធុង (ក្រឡាចត្រង្គ) មានមូលដ្ឋានការ៉េដែលមាន 4 ជ្រុងវែងស្មើគ្នា ហើយយើងមានបំណែកវែង 4 ដែលមានរាងដូចគ្នា។ ដូច្នេះមួយគួរតែដាក់ពួកគេនៅក្នុងស៊ីមេទ្រី. មានតែមួយបំណែករាងការ៉េពណ៌ស្វាយប៉ុណ្ណោះ។ ដើម្បីឱ្យមានដំណោះស្រាយស៊ីមេទ្រីបង្វិល 90° បំណែកនេះត្រូវតែនៅកណ្តាល។ កន្លែងផ្សេងទៀតនឹងបំបែកស៊ីមេទ្រី 90° នៃដំណោះស្រាយ។
- ល្បែងផ្គុំរូបដែលមានប៊ូតុងងងឹតតម្រូវឱ្យមានការគិតបន្ថែមទៀត. ចាប់ផ្តើមដោយការយល់ដឹងយ៉ាងពេញលេញអំពីល្បែងផ្គុំរូប "3×3×3 2" មុនពេលឈានទៅរកល្បែងផ្គុំរូប 5×5×5 ។
តើមនុស្សម្នាក់អាចដោះស្រាយល្បែងផ្គុំរូបទាំងនេះដោយមិនចាំបាច់សាកល្បងនិងកំហុសដោយរបៀបណា?
នេះគឺជាការណែនាំមួយចំនួន:
- បំបែកបញ្ហាលំបាកទៅជាបញ្ហាងាយស្រួលជាងមុន ពោលគឺទៅជាគោលដៅរង។ ឧទាហរណ៍ ដើម្បីបំពេញធុងទាំងមូល មនុស្សម្នាក់ត្រូវបំពេញស្រទាប់នីមួយៗ។
- រៀបចំបំណែកតាមវិធីស៊ីមេទ្រី ជាពិសេសប្រសិនបើធុងស៊ីមេទ្រីដូចជា 3×3×3 គូប ឬធុងរាងការ៉េ 1×7×7 ។
- ធ្វើឱ្យបានច្រើនបំផុតពីព័ត៌មានដែលបានផ្តល់ឱ្យ. តើបំណែកមានទំហំប៉ុន្មាន? តើមានប៉ុន្មាននាក់ក្នុងចំណោមពួកគេមានរូបរាងដូចគ្នា?
នៅសល់នៃ "Food for Thought" នេះមានគោលដៅដោះស្រាយល្បែងផ្គុំរូបទាំងអស់ដោយមិនចាំបាច់សាកល្បង និងកំហុស ដោយជំនួសមកជាមួយសំណួរសាមញ្ញ និងឆ្លើយពួកគេ។
និយមន័យ
សម្រាប់ភាពច្បាស់លាស់ នេះគឺជាពាក្យមួយចំនួនដែលយើងនឹងប្រើដើម្បីពិភាក្សាអំពីបញ្ហាវេចខ្ចប់៖
ដុំ
មួយក្នុងចំណោមរូបរាងដែលនឹងត្រូវបានដាក់បញ្ចូលគ្នាដើម្បីបង្កើតជារឹងធំជាង.
បំណែកសេសគឺជាបំណែកដែលមានប្រវែងសេសទាំងអស់ ដូចជា 1×1×1 ដុំ ឬ 1×3×5 ដុំ។
បំណែកគឺទោះបីជាវាមានប្រវែងយ៉ាងហោចណាស់ពីរដូចជា 1×2×4 ឬ 2×2×2 ។
តើបំណែកទាំងអស់ទាំងគូឬសេស?
ទេ. បំណែកដែលមានប្រវែងគូគ្នាពិតប្រាកដដូចជា 1×2×3 មិនសមនឹងនិយមន័យទាំងពីរទេ។ នៅក្នុងផ្នែកខាងក្រោម យើងនឹងផ្តោតលើបំណែកសេស និងគូ។
គូប/កុងតឺន័រ
គូបគឺជាព្រីសរាងចតុកោណ។ យើងប្រើពាក្យ "container" ដើម្បីសំដៅទៅលើសំបកទទេនៃ cuboid. យើងសំដៅទៅ "cuboid" ជាមាតិកានៃធុង។ ធុងមួយត្រូវបំពេញដោយបំណែក ហើយគូបត្រូវបានបង្កើតឡើងពីបំណែក។
ស្រទាប់
ស្រទាប់គឺជាចំណិតនៃកម្រាស់ 1 ក្នុងទិសដៅស្របទៅនឹងមុខនៃធុង។ កុងតឺន័រ 3×4×5 មាន 3 ស្រទាប់ទំហំ 4×5, 4 ស្រទាប់នៃទំហំ 3×5 និង 5 ស្រទាប់នៃទំហំ 3×4 ។
តើធុង 1×5×7 មានប៉ុន្មានស្រទាប់?
វាមានស្រទាប់ 5×7 មួយស្រទាប់ 1×7 ចំនួនប្រាំស្រទាប់ និងស្រទាប់ 1×5 ចំនួនប្រាំពីរ។ សរុបវាមាន 1 + 5 + 7 = 13 ស្រទាប់។
គូប
ជាពិសេស គូប 1×1×1 មិនមែនជាគូបធំជាងនោះទេ។ បំណែក 1×1×1 មាន 1 គូប ខណៈពេលដែលបំណែក 1×1×3 មាន 1 × 1 × 3 = 3 គូប។
ប្លុកអគារ
បំណែកមួយចំនួនភ្ជាប់គ្នាបង្កើតជាប្លុកអគារ. ប្លុកសាងសង់គួរឱ្យចាប់អារម្មណ៍នឹងមានស៊ីមេទ្រី. សម្រាប់ល្បែងផ្គុំរូបពិបាកជាងមុន ប្លុកសាងសង់ដូចគ្នា ឬកញ្ចក់ដូចគ្នាជាច្រើន បូករួមទាំងបំណែកកណ្តាលនឹងបំពេញធុង។
យុទ្ធសាស្រ្
ពាក់កណ្តាលនៃដំណោះស្រាយនៃបញ្ហាលំបាកគឺដើម្បីបំបែកបញ្ហាលំបាកទៅជាបញ្ហាតូចៗ.
ដើម្បីធ្វើដូចនេះ, មួយគួរតែសួរខ្លួនឯងសំណួរសាមញ្ញ. សំណួរខាងក្រោមនឹងមានប្រយោជន៍ក្នុងការដោះស្រាយល្បែងផ្គុំរូបវេចខ្ចប់។
តើរាល់គូបអាចត្រូវបានបង្កើតជាមួយនឹងបំណែកទំហំ 1×2×2 បានទេ? ឧទាហរណ៍ តើគូប 3×3×3 អាចត្រូវបានបង្កើតឡើងដោយប្រើតែបំណែកនៃទំហំ 1×2×2 ?
ទេ. បំណែក 1×2×2 មានចំនួនគូបគូ។ ដូច្នេះចំនួនណាមួយនៃ 1×2×2 បំណែកនឹងរួមគ្នាមានចំនួនគូបសរុបស្មើគ្នា។ ចាប់តាំងពីគូប 3×3×3 មានគូបចំនួនសេស វាមិនអាចបង្កើតតាមវិធីនេះបានទេ។
នៅក្នុងផ្នែកប៉ុន្មានបន្ទាប់ យើងនឹងស្វែងយល់ពីរបៀបដែលការបែងចែក ជាពិសេសដោយ 2 កំណត់ពីរបៀបដែលបំណែកត្រូវដាក់ដើម្បីដោះស្រាយល្បែងផ្គុំរូបមួយចំនួន។
យ៉ាងហោចណាស់ 1×2×2 បំណែកអាចបំពេញស្រទាប់ណាមួយនៃធុង 3×3×3 បានទេ?
ចម្លើយគឺម្តងទៀតទេ។ តំបន់នៅក្នុងស្រទាប់ដែលអាចត្រូវបានកាន់កាប់ដោយបំណែកមួយគឺជាផ្ទៃនៃមុខមួយនៃបំណែកនោះ, មែនទេ?
តើអ្វីទៅជាមុខនៃដុំ 1×2×2?
បំណែក 1×2×2 មានមុខ 1×2 ស្របគ្នាពីរគូ និងមុខ 2×2 មួយគូ។
តើមុខទាំងនេះមានអ្វីខ្លះ ហើយតើតំបន់ទាំងនោះមានអ្វីដូចគ្នា?
តំបន់គឺ 1 × 2 = 2 និង 2 × 2 = 4 ។ 2 និង 4 ទាំងពីរគឺជាលេខគូ។
យើងសង្កេតឃើញថាបំណែក 1×2×2 អាចកាន់កាប់បានតែចំនួនគូបគូ (2 ឬ 4) នៅក្នុងស្រទាប់នីមួយៗប៉ុណ្ណោះ។
តើនេះជាការពិតសម្រាប់បំណែកទាំងអស់?
មុខនីមួយៗនៃបំណែកមួយមានប្រវែងពីរ. ចាប់តាំងពីបំណែកគូមានប្រវែងសេសច្រើនបំផុតមួយ នោះមុខនីមួយៗនឹងមានប្រវែងគូយ៉ាងហោចណាស់មួយ។ ដោយសារតែ even × odd = even ផ្ទៃនៃមុខនីមួយៗនឹងមានគូ។ នេះជាមូលហេតុដែលយើងហៅពួកគេសូម្បីតែបំណែក!
យើងបានរៀនថា cuboids ដែលមានប្រវែងចំហៀងសេសមិនអាចបង្កើតឡើងពីបំណែកគូបានទេ។ ស្រទាប់ដែលមានផ្ទៃសេសមិនអាចបំពេញដោយបំណែកគូបានទេ។ ដូច្នេះ រូបផ្គុំរូប "3×3×3 2" មានបំណែក 1×1×1 មួយចំនួន ដែលជាបំណែកសេស។
នេះគឺជាសំណួរមានប្រយោជន៍មួយទៀតដើម្បីពិចារណា:
តើបំណែកមួយក្នុងចំណោមពីរប្រភេទ (1×1×1 និង 1×2×2) 'មានតម្លៃ' ជាងមួយទៀតទេ?
បាទ។ ប្រសិនបើយើងមានតែ 1×1×1 បំណែក នោះល្បែងផ្គុំរូបណាមួយនឹងតិចតួច តើអ្នកយល់ស្របទេ? ប្រសិនបើយើងមានតែ 1×2×2 បំណែក នោះធុងសេសមិនអាចបំពេញបានទេ ដូចដែលបានបង្ហាញខាងលើ។
សំណួរជាក់ស្តែងគឺ៖ តើចំនួនអប្បបរមានៃ 1×1×1 បំណែកដែលអាចបំពេញធុង 3×3×3 គឺជាអ្វី?
ជាធម្មតាសំណួរដូចខាងក្រោមកើតឡើង:
ហេតុអ្វីបានជាបី 1×1×1 គ្រប់គ្រាន់?
ដើម្បីឆ្លើយសំណួរនេះ យើងនឹងប្រៀបធៀបចំនួនស្រទាប់សេស (layers with odd area) ទៅនឹងចំនួនស្រទាប់តំបន់សេសដែលអាចបំពេញដោយបំណែកគូ និងមានតែ 3 គូបប៉ុណ្ណោះ។
តើធុង 3×3×3 មានប៉ុន្មានស្រទាប់?
នៅក្នុងទិសដៅនីមួយៗនៃទិសទាំងបី (ទទឹង, កម្ពស់, ជម្រៅ), ធុងមាន 3 ស្រទាប់. មាន 3 + 3 + 3 = 9 ស្រទាប់សេសដែលត្រូវបានបំពេញនៅពេលធុងត្រូវបានបំពេញ។
តើស្រទាប់ 3×3 សេសប៉ុន្មានស្រទាប់អាចបញ្ចប់បានជាមួយនឹង 1×1×1 ដុំតែមួយ (និងខ្លះសូម្បីតែ 1×2×2 បំណែក)?
បីស្រទាប់៖ ស្រទាប់ផ្ដេក និងស្រទាប់បញ្ឈរពីរដែលមានបំណែក 1×1×1 ។ ដូច្នេះ 3 គូបអាចជួយបំពេញបានច្រើនបំផុត 3 &ដង 3 = 9 ស្រទាប់។
នេះបង្ហាញថា 3 គូបគឺចាំបាច់ ហើយដោយសារតែរូបផ្គុំ "3×3×2 2" អាចដោះស្រាយបាន 3 គូបក៏គ្រប់គ្រាន់ដើម្បីបំពេញស្រទាប់សេសទាំង 9 ផងដែរ។
តើវាប្រាប់យើងអំពីទីតាំងនៃ 3 គូបនៅក្នុង
ល្បែងផ្គុំរូប "3×3×3 2"?
នៅក្នុងស្រទាប់នីមួយៗនៃ 9 អាចមានតែ 1 គូប, មិនមែន 0 គូបនិងមិនមែន 2 គូប! បើមិនដូច្នេះទេ 3 គូបនឹងមិនគ្រប់គ្រាន់សម្រាប់ 9 ស្រទាប់ទេ។
នេះគឺជារបកគំហើញសម្រាប់ដំណោះស្រាយ។ លើសពីនេះទៅទៀត វិធីតែមួយគត់ដើម្បីដាក់គូបគឺនៅតាមបណ្តោយអង្កត់ទ្រូង - ជាមួយនឹងគូបមួយនៅកណ្តាល និងគូបពីរផ្សេងទៀតនៅជ្រុងផ្ទុយគ្នាអង្កត់ទ្រូង។ បើមិនដូច្នេះទេ បំណែកសំពោងសំពោង 1×2×2 នឹងធំពេកដើម្បីបំពេញចន្លោះជុំវិញ 3 គូប។
ដូច្នេះ, ដាក់គូបមួយនៅជ្រុងមួយ, និងបី 1×2×2 បំណែកនៅក្នុងវិធីស៊ីមេទ្រីនៅជុំវិញគូបនោះ. ដាក់គូបមួយនៅកណ្តាល, មួយនៅជ្រុងផ្ទុយគ្នា, ហើយនៅសល់នឹងច្បាស់លាស់.
តើយើងអាចរៀនអ្វីផ្សេងទៀតពីដំណោះស្រាយនេះ? ឧទាហរណ៍ តើវាមានស៊ីមេទ្រីទេ?
ស៊ីមេទ្រីអាចមើលឃើញបន្ទាប់ពីដាក់គូបដំបូងនៅជ្រុង និងបំណែក 1×2×2 ទាំងបីនៅជុំវិញវា។ ដំណោះស្រាយមានស៊ីមេទ្រីបង្វិល 120° ជាមួយនឹងអង្កត់ទ្រូងនៃគូបជាអ័ក្សបង្វិល (120° = 1/3 នៃការបង្វិលរង្វង់ពេញ)។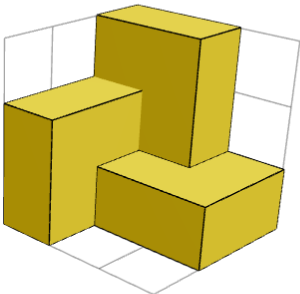
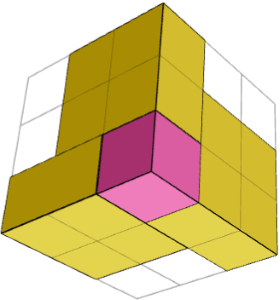
តើដំណោះស្រាយគឺជាផលបូកនៃប្លុកសាងសង់ដូចគ្នា ឬស៊ីមេទ្រី ដែលនីមួយៗមានបំណែកជាច្រើន?
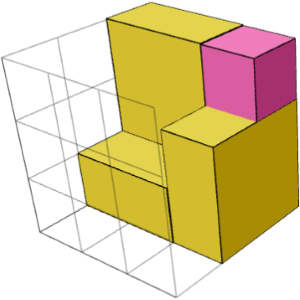
បាទ។ គូបគឺជាផលបូកនៃប្លុកសាងសង់ 2 ដែលជាកញ្ចក់ស៊ីមេទ្រី (1 គូបនៅជ្រុង + បី 1×2×2 បំណែកជុំវិញវា) និងគូបមួយនៅកណ្តាល។ រូបភាពទាំង 2 ខាងលើបង្ហាញពីប្លុកអគារមួយពី 2 ជ្រុង។
តើមានវិធីផ្សេងទៀតដើម្បីដោះស្រាយរូបផ្គុំនេះដោយប្រើប្លុកអាគារផ្សេងៗគ្នាដែរឬទេ?
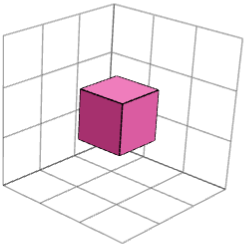
បាទ។ រូបភាពខាងឆ្វេង និងខាងស្តាំខាងក្រោមបង្ហាញប្លុកសាងសង់ស៊ីមេទ្រីកញ្ចក់ពីរសម្រាប់រូបផ្គុំ "3×3×3 2" ។ ពួកគេអាចត្រូវបានរួមបញ្ចូលគ្នាជាមួយគូបកណ្តាល (រូបភាពកណ្តាល) ដើម្បីដោះស្រាយរូបផ្គុំ។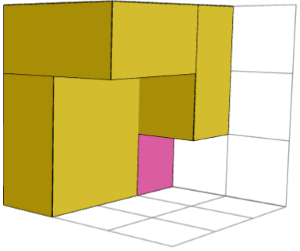
ហេតុអ្វីបានជាយើងគួររំខានគិតអំពីប្លុកសាងសង់?
វាមានភាពងាយស្រួលក្នុងការប្រើចំនួនតូចនៃបំណែកដែលបានផ្តល់ឱ្យនិងបង្កើតអ្វីមួយស៊ីមេទ្រីពីពួកគេ, ជាងការបំពេញធុងធំជាមួយនឹងបំណែកទាំងអស់.
តើប្លុកសាងសង់អាចត្រូវបានប្រើដើម្បីដោះស្រាយល្បែងផ្គុំរូបធំៗដូចជា "3×5×7 1" បានទេ?
បាទ។ ធុងធំជាង ទោះបីជាប្រវែងរបស់វាខុសគ្នាក៏ដោយ អាចត្រូវបានបំពេញដោយប្រើប្លុកសាងសង់ស៊ីមេទ្រីដូចគ្នា/កញ្ចក់។ មានវិធីជាច្រើនក្នុងការដោះស្រាយល្បែងផ្គុំរូប "3×5×7 1" ដោយប្រើប្លុកសាងសង់ និងបំណែកសេសកណ្តាល។ យើងទុកវាឱ្យអ្នកដើម្បីស្វែងរកឧទាហរណ៍មួយចំនួន។
តើយើងដឹងដោយរបៀបណាថាបំណែកណាដែលគួរបង្កើតជាប្លុកសាងសង់?
អនុញ្ញាតឱ្យយើងគិតអំពីកណ្តាលនៃ cuboid សេសជាមុនសិន។ ដោយសារតែទីតាំងកណ្តាលមានតែមួយគត់ ប្រសិនបើយើងចង់បានដំណោះស្រាយស៊ីមេទ្រី កណ្តាលត្រូវតែត្រូវបានកាន់កាប់ដោយបំណែកដែលមានរាងដូចគ្នានឹងធុង។ គូប 3×3×3 គឺជាគូប ដូច្នេះបំណែកកណ្តាលសម្រាប់វាត្រូវការជាគូប។ បំណែក 1×2×2 នៅកណ្តាលនឹងបំបែកស៊ីមេទ្រី។
នេះមានន័យថាយើងមាន 6 ពណ៌លឿង និង 3 − 1 = 2 បំណែកពណ៌ផ្កាឈូកដើម្បីសាងសង់ប្លុកសាងសង់ដូចគ្នាមួយចំនួន។
តើយើងគួរព្យាយាមបង្កើតប្លុកសាងសង់ប៉ុន្មាន?
ប្លុកសាងសង់គួរតែបង្កើតជាគូបដកបំណែកកណ្តាល។ ដូច្នេះ ចំនួនបំណែកពណ៌លឿងនៅក្នុងប្លុកអាគារត្រូវតែជាបែងចែក 6 (ចំនួនសរុបនៃប្លុកពណ៌លឿង) ហើយចំនួនបំណែកពណ៌ផ្កាឈូកនៃប្លុកអាគារត្រូវបែងចែក 2 (ចំនួនគូបពណ៌ផ្កាឈូកដែលនៅសល់បន្ទាប់ពីកក់ទុកមួយសម្រាប់កណ្តាល)។
ដូច្នេះ លេខ N នៃប្លុកអាគារដូចគ្នាគឺជាគុណទូទៅដ៏ធំបំផុតនៃចំនួនបំណែកដូចគ្នានៅទីនេះ 6 និង 2 ដែលជា GCD(6,2) = 2 ។ ដូច្នេះយើងគួរតែបង្កើតប្លុកសាងសង់ពី 2 / 2 = 1 គូបពណ៌ផ្កាឈូក និង 6 / 2 = 3 ប្លុកពណ៌លឿង។ នេះគឺជាអ្វីដែលយើងបានធ្វើ.
សង្ខេបក្បួនដោះស្រាយគណិតវិទ្យាដើម្បីប្រើវាសម្រាប់ល្បែងផ្គុំរូបធំជាង។
សម្រាប់ធុងសេស៖
- Align the odd pieces to make sure they are not overlapping in any layer. ពួកគេគួរតែភ្ជាប់ជ្រុងមួយនៃធុងជាមួយជ្រុងផ្ទុយគ្នានៃធុង។ ប្រសិនបើបំណែកសេសគឺជាគូប, ពួកគេបង្កើតជាអង្កត់ទ្រូង. ប្រសិនបើបំណែកសេសមានទំហំធំជាង (1x1x3) នោះពួកវាបង្កើតជាអង្កត់ទ្រូងដែលមិនមែនត្រង់។
- ប្រសិនបើមានតែមួយប្រភេទនៃបំណែកស្មើគ្នា បន្ទាប់មកប្រើវាដើម្បីបំពេញធុង។
- ប្រសិនបើមានប្រភេទផ្សេងៗគ្នានៃបំណែកសូម្បីតែ៖
- ដាក់បំណែកសេសកណ្តាល។ ពីបំណែកដែលនៅសល់ ស្វែងរកបែងចែកទូទៅធំបំផុត N នៃចំនួនបំណែកនៃប្រភេទផ្សេងៗគ្នា។ N គឺជាចំនួននៃប្លុកអគារ។
- បង្កើតប្លុកសាងសង់ដូចគ្នា N ហើយដាក់វាជាមួយបំណែកកណ្តាលក្នុងករណីធុងសេស។
ខណៈពេលដែលល្បែងផ្គុំរូបតូចៗអាចត្រូវបានដោះស្រាយយ៉ាងងាយស្រួលដោយការសាកល្បង និងកំហុស យុទ្ធសាស្រ្តនេះមិនដំណើរការសម្រាប់ល្បែងផ្គុំរូបធំជាងនេះទេ។ ការរុករករបស់យើងនៃបំណែកសេសនិងគូបង្ហាញពីហេតុផលសំខាន់មួយ: ការដាក់បំណែកសេសគឺសំខាន់ណាស់, ព្រោះមានវិធីតិចតួចណាស់ដែលពួកគេអាចត្រូវបានដាក់ត្រឹមត្រូវ. ដោយប្រើការសាកល្បងនិងកំហុស, one can make a mistake right at the start and only realize that something went wrong after placed many pieces. នេះធ្វើឱ្យវាពិបាកមិនគួរឱ្យជឿក្នុងការកំណត់អ្វីដែលបណ្តាលឱ្យមានកំហុស ដូច្នេះមិនមានមតិយោបល់ដែលអាចប្រើបានទេ; វិធីសាស្រ្តសាកល្បងនិងកំហុសមិនមានប្រសិទ្ធភាពសម្រាប់ធុងធំជាងនេះទេ។ ការគិតត្រូវបានទាមទារ។
ការវេចខ្ចប់ដោយមានតែមួយប្រភេទនៃបំណែក
នៅក្នុងផ្នែកនេះ យើងនឹងស្វែងយល់ពីទំហំនៃ cuboids ដែលអាចត្រូវបានបង្កើតឡើងពីប្រភេទតែមួយនៃបំណែក។ នេះគឺជាផ្នែកទ្រឹស្តី មិនចាំបាច់សម្រាប់ការដោះស្រាយល្បែងផ្គុំរូបខាងលើទេ។ ផ្នែកនេះមិនតម្រូវឱ្យមានគណិតវិទ្យាពិបាកទេ។
ជាមួយនឹងបំណែក 1×1×1 គ្រប់គ្រាន់ យើងអាចបង្កើតបានយ៉ាងងាយស្រួលនូវគូបដែលមានទំហំណាមួយ។ ប៉ុន្តែចុះបំណែកផ្សេងទៀតដូចជា 2×3×4 ឬ 1×2×5 ដុំ? មានសំណួរសំខាន់ពីរដែលត្រូវស៊ើបអង្កេត។ ទីមួយ ដោយសារប្រវែងនៃបំណែក និងប្រវែងនៃគូប តើយើងអាចកំណត់ដោយរបៀបណាថាតើ cuboid អាចត្រូវបានបង្កើតពីច្បាប់ចម្លងនៃបំណែកនោះ? ទីពីរ តើយើងអាចបង្កើតប្រវែងនៃគូបដែលអាចបង្កើតបានដោយរបៀបណា? ពេញមួយផ្នែកនេះ យើងនឹងពិចារណាសំណួរសាមញ្ញៗ ខណៈពេលស្វែងយល់ពីបញ្ហាសំខាន់ទាំងពីរនេះ។
តើគូប 2×6×10 អាចត្រូវបានបង្កើតឡើងពីតែ 1×2×5 បំណែកបានទេ?
បាទ! បំណែក 1×2×5 ចំនួនបីអាចត្រូវបានដាក់ជាប់គ្នាដើម្បីបង្កើតជារាង 1×6×5 (3 × 2 = 6) ។ បន្ទាប់មកយើងអាចបង្កើតរូបរាង 1×6×5 ទីពីរ ហើយរួមបញ្ចូលពួកវាទៅជារូបរាង 1×6×10 ។ ជាចុងក្រោយ រាង 1×6×10 ពីរអាចត្រូវបានដាក់ជាមួយគ្នាដើម្បីបង្កើតជាគូប 2×6×10 ។
តើវាអាចទៅរួចទេក្នុងការបង្កើតគូប 10×12×14 ដោយប្រើតែបំណែកនៃទំហំ 2×5×6 ?
ជំនួយ
វាមិនចាំបាច់ស្រមៃថាតើបំណែកនេះនឹងត្រូវបានរៀបចំយ៉ាងដូចម្តេច.
គន្លឹះមួយទៀត?
បំណែក 2×5×6 គឺដូចគ្នាទៅនឹងបំណែក 5×6×2 ចាប់តាំងពីវាអាចបង្វិលបាន។
ចម្លើយ
បាទ។ ចាប់តាំងពី 10 / 5 = 2, 12 / 6 = 2 និង 14 / 2 = 7 គូបធំជាងនេះអាចត្រូវបានគិតថាជាការរៀបចំ 2×2×7 នៃបំណែក 5×6×2 ។ បំណែក 5×6×2 ទាំងអស់អាចត្រូវបានដាក់ជាមួយនឹងការតម្រង់ទិសដូចគ្នា។
តើយើងអាចទូទៅការរកឃើញទាំងនេះដោយរបៀបណា?
ឧបមាថាយើងមានតែបំណែកនៃទំហំ x & times y & times z ប៉ុណ្ណោះ។ បន្ទាប់មកការបង្កើត X & ដង Y & ដង Z cuboid គឺអាចធ្វើទៅបានប្រសិនបើមានចំនួនគត់វិជ្ជមាន A, B, C ដូច្នេះ Ax, By និង Cz ស្មើនឹង X, Y និង Z តាមលំដាប់មួយចំនួន។
តើមានប៉ុន្មានបំណែកនឹងត្រូវបានប្រើក្នុងករណីនេះ?
យើងអាចរៀបចំបំណែក A ក្នុងទិសដៅមួយ B ក្នុងទិសដៅមួយទៀត និង C ក្នុងទិសដៅទីបី។ សរុប A × B & times បំណែក C នឹងត្រូវបានប្រើ។
ហេតុអ្វីបានជា Ax, By និង Cz អាចស្មើនឹង X, Y និង Z តាមលំដាប់ណាមួយ?
ធុងដែលមានទំហំ X &ដង Y &ដង Z គឺដូចគ្នានឹង Z &ដង X &ដង Y គូបដែរ។ លំដាប់នៃប្រវែងមិនមានបញ្ហាទេព្រោះ cuboid អាចត្រូវបានបង្វិល។
តើវាជាការពិតទេដែលគូបណាមួយដែលបង្កើតឡើងពី 1×2×3 បំណែកត្រូវតែមានប្រវែង A, B × 2, C × 3 សម្រាប់ចំនួនគត់វិជ្ជមានមួយចំនួន A, B, C ?
ទេ. ប្រសិនបើបំណែក 1×2×3 ទាំងអស់ត្រូវបានតម្រង់ទិសក្នុងទិសដៅដូចគ្នា គូបនឹងមានទំហំ A × (B × 2) × (C × 3) ។ ប៉ុន្តែបំណែកអាចត្រូវបានតម្រង់ទិសខុសគ្នា ហើយនៅតែបង្កើតជាគូប។ ឧទាហរណ៍ បំណែក 1×2×3 អាចបង្កើតជាគូប 1×5×6 ទោះបីជា 1, 5 និង 6 មិនស្មើនឹង A, B × 2 និង C × 3 តាមលំដាប់ណាមួយក៏ដោយ។ ឧទាហរណ៍មួយទៀតគឺរូបផ្គុំរូប "1×7×10 1" ដែលមានបំណែក 1×2×5 ។
តើអ្វីជាទំនាក់ទំនងរវាងប្រវែងរបស់បំណែក និងប្រវែងរបស់ cuboid ក្នុងឧទាហរណ៍ទាំងពីរនេះ?
នៅក្នុងឧទាហរណ៍ទាំងពីរនេះ ប្រវែងមួយនៃគូបគឺជាផលបូកនៃប្រវែងពីរនៃបំណែក។ ប្រវែងខុសគ្នានៃ cuboid គឺ LCM (Lowest Common Multiple) នៃប្រវែងពីរដូចគ្នានៃបំណែក។ ក្នុងករណីគូប 1×5×6 ដែលបង្កើតឡើងពី 1×2×3 បំណែកយើងមាន 1×5×6 = 1 × (2 + 3) × LCM(2,3) ។ ស្រដៀងគ្នានេះដែរ 1×7×10 = 1 × (2 + 5) × LCM(2,5) ។
តើយើងអាចប្រើការពិតនេះដើម្បីស្វែងរកវិធីបង្កើតប្រវែងនៃ cuboids ដែលអាចត្រូវបានសាងសង់ពីបំណែកដែលបានផ្តល់ឱ្យដោយរបៀបណា?
យើងចាប់ផ្តើមដោយតំណាងឱ្យប្រវែងនៃបំណែកជាបីដង។ ឧទាហរណ៍ បំណែក 1×2×3 ត្រូវបានតំណាងដោយ (1, 2, 3) ។ ឥឡូវនេះមានប្រតិបត្តិការ 3 ដែលយើងអាចធ្វើម្តងហើយម្តងទៀតដើម្បីផ្តល់ប្រវែងនៃ cuboids ដែលអាចត្រូវបានបង្កើតឡើងពីបំណែកនេះ។ ពួកគេគឺ:
- ផ្លាស់ប្តូរលំដាប់នៃប្រវែង។ នេះត្រូវបានគេស្គាល់ថាជាការផ្លាស់ប្តូរ ។ ក្នុងករណីរបស់យើង វាតំណាងឱ្យការបង្វិលនៅក្នុងចន្លោះ 3 វិមាត្រ។ ឧទាហរណ៍គឺ
(1, 2, 3) → (2, 3, 1) ។ - គុណប្រវែងដោយចំនួនគត់វិជ្ជមាន A, B និង C រៀងគ្នា។ នេះត្រូវគ្នាទៅនឹងការបង្កើតគូបធំជាងដោយដាក់បំណែក A ក្នុងទិសដៅមួយ B ក្នុងទិសដៅមួយទៀត និង C តាមទិសដៅទីបី។ ឧទាហរណ៍ យើងអាចគុណជាមួយ 1, 4, និង 3 ដើម្បីផ្តល់ (1, 2, 3) → (1 × 1, 4 × 2, 3 × 3) = (1, 8, 9) ។
- យកប្រវែងពីរហើយជំនួសមួយជាមួយនឹងផលបូករបស់ពួកគេនិងមួយជាមួយ LCM របស់ពួកគេ។. នេះត្រូវគ្នាទៅនឹងការបង្កើតគូបធំជាងជាមួយនឹងបំណែកតម្រង់ទិសផ្សេងៗគ្នា។ ឧទាហរណ៍ ការជ្រើសរើសប្រវែង 2 និង 3 យើងនឹងទទួលបាន (1, 2, 3) → (1, 2 + 3, LCM(2,3)) = (1, 5, 6) ។
តើមនុស្សម្នាក់អាចរួមបញ្ចូលគ្នានូវបំណែកតាមវិធីទី 4 ដើម្បីបង្កើត cuboid ដែលមានរូបរាងខុសពីលទ្ធផលនៃប្រតិបត្តិការទី 3 បានទេ?
បាទ។ ពិចារណាបំណែកនៃទំហំ x &ដង y &ដង z ។ ប្រតិបត្តិការទីបីបង្កើតគូបដែលមានទំហំ x &ដង (y + z) &ដង LCM(y,z) ដែលប្រវែងមួយ x មិនផ្លាស់ប្តូរពីបំណែកទៅគូប។
វិធីស្រដៀងគ្នាប៉ុន្តែខុសគ្នានឹងត្រូវដាក់ម្តងទៀត LCM(y,z)/y បំណែកជាច្រើននៅជាប់គ្នា និង LCM(y,z)/y បំណែកជាច្រើននៅជាប់គ្នាដូចមុន ប៉ុន្តែឥឡូវនេះដើម្បីបង្វិលមួយឈុតដោយ 90° ដូច្នេះប្លុកទាំងពីរមានប្រវែងដូចគ្នា LCM(y,z) ប៉ុន្តែកម្ពស់ខុសគ្នា។ នៅក្នុងលក្ខខណ្ឌគណិតវិទ្យា យើងមិនភ្ជាប់ x × y × LCM(y,z) និង x × z × LCM(y,z) ដើម្បីបង្កើត x × (y + z) × LCM(y,z) ។ ផ្ទុយទៅវិញ មួយក្នុងចំណោមពួកវានិយាយថា x × z × LCM(y,z) ត្រូវបានបង្វិលទៅ z × x × LCM(y,z) ហើយបន្ទាប់មកភ្ជាប់។
ផ្ទៃមូលដ្ឋានរាងចតុកោណបន្ទាប់មកមិនមែន (y + z) &ដង LCM(y,z) ប៉ុន្តែជា (x + z) &ដង LCM(y,z) ។ បន្ទាប់មកប្លុកអគារទាំងពីរ x × y × LCM(y,z) និង z × x × LCM(y,z) មានប្រវែង x និង z រៀងគ្នាក្នុងទិសដៅ X ។
ជង់ LCM(x,z)/x ប្លុកអគារជាច្រើននៃកម្ពស់ x និង LCM(x,z)/z ប្លុកអគារជាច្រើននៃកម្ពស់ z ជង់ទាំងពីរឈានដល់កម្ពស់ LCM(x,z) ។ នៅពេលដែលពួកវាត្រូវបានភ្ជាប់ លទ្ធផលគឺគូបដែលមានទំហំ LCM(x,z) × (x + z) × LCM(y,z) ដែលមានរូបរាង និងទំហំខុសពីគូបណាមួយដែលបណ្តាលមកពីប្រតិបត្តិការទីបី។
មនុស្សម្នាក់អាចធ្វើម្តងទៀតប្រតិបត្តិការទាំងនេះតាមលំដាប់ណាមួយ ដំបូងបង្កើត cuboid ពីបំណែកមួយ ហើយបន្ទាប់មកប្រើ cuboid ជា "បំណែក" ដើម្បីបង្កើត cuboid កាន់តែធំជាងនេះ។ យើងបានពិភាក្សាពីមុនពីរបៀបដែលគូប 2×6×10 អាចត្រូវបានបង្កើតឡើងពី 1×2×5 បំណែក។ ក្នុងករណីនេះត្រូវការប្រតិបត្តិការតែមួយប៉ុណ្ណោះ ដោយគុណដោយ 2, 3 និង 2 រៀងគ្នា៖ (1, 2, 5) → (2 × 1, 3 × 2, 2 × 5) = (2, 5, 10) ។
ដូច្នេះបំណែកនៃទំហំ x × y × z មិនត្រឹមតែអាចសាងសង់គូបដែលមានទំហំ Ax × By × Cz ប៉ុណ្ណោះទេ ប៉ុន្តែឧទាហរណ៍ក៏មានទំហំ x × (y + z) × LCM(y,z) ដែល LCM(y,z) គឺជាពហុទូទៅទាបបំផុតនៃ y និង z ។ ការដាក់ប្លុកសាងសង់ជាច្រើននេះរួមគ្នាផ្តល់ឱ្យគូបដែលមានទំហំ Ax × B(y + z) + C(LCM(y,z)) ។
ឥឡូវនេះយើងនឹងពិចារណាប្រភេទពិសេសនៃបំណែក. បំណែកមួយគឺ harmonic ប្រសិនបើប្រវែងធំរបស់វានីមួយៗត្រូវបានបែងចែកដោយប្រវែងតូចបន្ទាប់។ ឧទាហរណ៍ បំណែក 1×2×6 គឺ harmonic ចាប់តាំងពី 2 / 1 = 1 និង 6 / 2 = 3 ។ បំណែក 1×4×6 មិនមែនជា harmonic ចាប់តាំងពី 6 មិនមែនជាគុណនៃ 4 ។
តើ 1×2×3 បំណែក harmonic មែនទេ?
ទេ ព្រោះ 3 មិនអាចបែងចែកដោយ 2 បានទេ។
តើអ្វីធ្វើឱ្យបំណែក harmonic ពិសេសក្នុងការវេចខ្ចប់? តើពួកគេទាក់ទងនឹងការពិភាក្សារបស់យើងអំពីប្រវែងនៃបំណែកនិងគូបយ៉ាងដូចម្តេច?
យើងបានសង្កេតឃើញរួចហើយថាបំណែកណាមួយអាចបង្កើតជាគូបដែលមានប្រវែងច្រើននៃប្រវែងរបស់បំណែក។ វាប្រែចេញថាប្រវែងនៃគូបណាមួយដែលបង្កើតឡើងដោយបំណែកអាម៉ូនិកដូចគ្នាត្រូវតែមានច្រើននៃប្រវែងបំណែក។ នោះគឺប្រសិនបើបំណែក harmonic មានប្រវែង x, y និង z គូបណាមួយដែលបង្កើតឡើងពីច្បាប់ចម្លងនៃបំណែកនេះត្រូវតែមានប្រវែងមួយដែលអាចបែងចែកដោយ x មួយទៀតអាចបែងចែកដោយ y និងទីបីបែងចែកដោយ z ។ ខណៈពេលដែលនេះជាសេចក្តីថ្លែងការណ៍សាមញ្ញ ភស្តុតាងទាមទារគំនិតលើសពីវិសាលភាពនៃគេហទំព័រនេះ។ តំណភ្ជាប់ទៅកាន់ភស្តុតាងអាចរកបាននៅក្នុងផ្នែក "ការទទួលស្គាល់"។
តើការពិតនេះស្របនឹងប្រតិបត្តិការទាំងបួនដែលយើងបានពិភាក្សាខាងលើយ៉ាងដូចម្តេច?
យើងអាចចាប់ផ្តើមដោយគិតថាបំណែកមួយក៏ជា cuboid ដែលបង្កើតឡើងពីច្បាប់ចម្លងមួយនៃបំណែកនោះ។ បំណែក x & times y & times z ក៏ជា x & times y & times z cuboid ផងដែរ។ ប្រវែងនៃ cuboid នេះគឺជាគុណនៃប្រវែងរបស់បំណែក ព្រោះលេខនីមួយៗគឺជាគុណនៃខ្លួនវា។ យើងនឹងបង្ហាញពីមូលហេតុដែលវិធីសាស្រ្តទាំងបួនដែលយើងបានណែនាំផលិត cuboids ដែលមានប្រវែងនៅតែច្រើននៃប្រវែងរបស់បំណែក។
- ការផ្លាស់ប្តូរលំដាប់នៃប្រវែង (permutation): នេះគ្រាន់តែជាការបង្វិល ហើយពិតជាមិនផ្លាស់ប្តូរប្រវែងនៃ cuboid នោះទេ។ ប្រវែងនៃ cuboid នឹងនៅតែមានច្រើននៃប្រវែងរបស់បំណែក។
- ការគុណប្រវែងនៃ cuboid ដោយចំនួនគត់វិជ្ជមាន៖ ប្រសិនបើប្រវែងនៃ cuboid គឺជាគុណនៃប្រវែងរបស់បំណែករួចហើយ វានឹងមិនផ្លាស់ប្តូរទេ។ ពួកគេនឹងក្លាយជាច្រើនជាង។ ប្រសិនបើ X = Ax គឺជាគុណនៃ x បន្ទាប់មក DX = DAx ក៏ជាគុណនៃ x សម្រាប់ចំនួនគត់វិជ្ជមាន D ។
- ការជំនួសប្រវែងពីរដោយផលបូកនិង LCM របស់ពួកគេ: នេះជាមូលហេតុដែលបំណែក harmonic មានសារៈសំខាន់; យើងនឹងត្រូវប្រើនិយមន័យនៃបំណែកអាម៉ូនិក។ ឧបមាថាយើងបានចាប់ផ្តើមជាមួយនឹងបំណែកអាម៉ូនិក (x, y, z) ដែលយើងបានបង្កើតគូប (Ax, By, Cz) រួចហើយ។ លំដាប់នៃប្រវែងមិនមានបញ្ហាទេចាប់តាំងពី cuboid អាចត្រូវបានបង្វិល។ ឥឡូវនេះយើងនឹងធ្វើប្រតិបត្តិការទីបីលើប្រវែងគូបពីរណាមួយ និយាយថា Ax និង By: (Ax, By, Cz) → (Ax + By, LCM(Ax,By), Cz) ។ ឥឡូវនេះចាប់តាំងពីបំណែក (x, y, z) គឺ harmonic មួយក្នុងចំណោមប្រវែងពីរ x និង y គឺជាច្រើននៃផ្សេងទៀត។ ឧបមាថា y គឺជាគុណនៃ x ។ ដូច្នេះ By ក៏ជាគុណនៃ x ផងដែរ ហើយចាប់តាំងពី Ax ក៏ដូចគ្នា ផលបូក Ax + By គឺជាគុណនៃ x ។ បន្ទាប់មក LCM(Ax,By) គឺជាច្រើនទូទៅទាបបំផុតនៃ Ax និង By ដូច្នេះវាគឺតាមនិយមន័យច្រើននៃ By ដូច្នេះវាអាចបែងចែកដោយ y ។ ជាចុងក្រោយ Cz គឺជាការពិតណាស់ច្រើននៃ z ។ ដូច្នេះ ប្រវែងនៃគូបថ្មី (Ax + By, LCM(Ax,By), Cz) នៅតែជាពហុនៃប្រវែងរបស់បំណែក។
- ចុះប្រតិបត្តិការទីបួនវិញ? ដោយសារតែប្រតិបត្តិការនេះស្រដៀងទៅនឹងប្រតិបត្តិការទីបី អាគុយម៉ង់ដែលបានបង្ហាញខាងលើអាចត្រូវបានកែសម្រួលសម្រាប់ករណីនេះ។ យើងទុកវាជាលំហាត់ប្រាណ។
យើងបានបង្ហាញថាប្រតិបត្តិការទាំងបួនដែលធ្វើម្តងហើយម្តងទៀតក្នុងលំដាប់ណាមួយនៅលើបំណែកអាម៉ូនិកណាមួយនឹងបណ្តាលឱ្យមានគូបដែលមានប្រវែងច្រើននៃប្រវែងរបស់បំណែក។ វាជារឿងសំខាន់ក្នុងការកត់សម្គាល់ថានៅក្នុងការពិភាក្សារបស់យើងអំពីប្រតិបត្តិការទីបី (និងទីបួន!), យើងពឹងផ្អែកលើការពិតដែលថាបំណែកនេះគឺ harmonic. នៅពេលដែលបំណែកមួយមិនមែនជា harmonic, អាគុយម៉ង់បរាជ័យ. នេះគឺជាភាពខុសគ្នាសំខាន់រវាងបំណែក harmonic និង non-harmonic ។ សម្រាប់បំណែក harmonic វិធីសាស្រ្តទីបី និងទីបួនមិនបង្កើតរាងបន្ថែមបើប្រៀបធៀបទៅនឹងវិធីសាស្រ្តពីរដំបូង។
ជាលទ្ធផល cuboid ណាមួយដែលបង្កើតឡើងពីបំណែក harmonic អាចមានបំណែកទាំងអស់នៅក្នុងទិសដៅដូចគ្នា។ ដូច្នេះ ប្រសិនបើយើងកំពុងព្យាយាមបង្កើត cuboid ពីបំណែក harmonic ដូចគ្នា វាគ្រប់គ្រាន់ដើម្បីព្យាយាមរៀបចំពួកវាទាំងអស់ប្រឈមមុខនឹងទិសដៅតែមួយ។ ប្រសិនបើវាមិនអាចទៅរួចនោះ cuboid មិនអាចបង្កើតបានទាល់តែសោះ។
ចាប់តាំងពីបំណែក 1×2×2 គឺ harmonic គូបណាមួយដែលបង្កើតឡើងពីច្បាប់ចម្លងនៃបំណែកនេះត្រូវតែមានប្រវែង A, B × 2 និង C × 2 សម្រាប់ចំនួនគត់មួយចំនួន A, B និង C ។ រូបភាពខាងក្រោមបង្ហាញគូប 5×4×4 ដែលបង្កើតឡើងដោយ 1×2×2 បំណែកដែលសុទ្ធតែមានទិសដៅដូចគ្នា។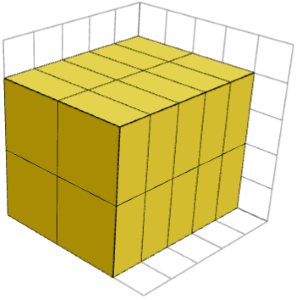
តើ A, B និង C មានតម្លៃអ្វីខ្លះ?
ការកំណត់ A, B × 2 និង C × 2 ស្មើនឹង 5, 4 និង 4 រៀងគ្នា យើងរកឃើញ A = 5 / 1 = 1, B = 4 / 2 = 2 និង C = 4 / 2 = 2 ។
នៅពេលវេចខ្ចប់ជាមួយបំណែក harmonic តើបំណែកត្រូវប្រឈមមុខនឹងទិសដៅដូចគ្នាដែរឬទេ?
ទេ! ទោះបីជាវាតែងតែអាចធ្វើទៅបានសម្រាប់បំណែកទាំងអស់ដើម្បីមានការតម្រង់ទិសដូចគ្នាក៏ដោយ ក៏អាចមានការរៀបចំផ្សេងទៀត ប៉ុន្តែពួកវាមិនបង្កើតរូបរាងថ្មីទេ។ រូបភាពខាងក្រោមបង្ហាញពីវិធីផ្សេងគ្នាដើម្បីបង្កើតគូប 5×4×4 ពី 1×2×2 បំណែក។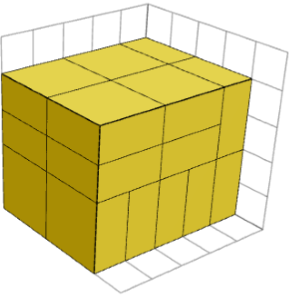
តើច្បាប់សម្រាប់បំណែកដែលមិនមែនជា harmonic មានអ្វីខ្លះ?
នៅពេលធ្វើការជាមួយបំណែកដែលមិនមែនជា harmonic x × y & times z មានគូបមួយចំនួនដែលអាចត្រូវបានបង្កើតឡើងដែលមានទំហំមិនមែនជា Ax × By × Cz សម្រាប់ចំនួនគត់ណាមួយ A, B, C ។ ឧទាហរណ៍ គូប 1×5×6 អាចត្រូវបានបង្កើតពី 1×2×3 បំណែក។ នេះគឺជាលទ្ធផលនៃប្រតិបត្តិការទីបី ដូចដែលបានពិភាក្សាពីមុន។
វាជារឿងសំខាន់ក្នុងការកត់សម្គាល់ថាចំនួនគូបនៅក្នុង cuboid ត្រូវតែបែងចែកដោយចំនួនគូបនៅក្នុងបំណែក។ នៅពេលដែលប្រវែងនៃគូបមិនមែនជាគុណនៃប្រវែងខុសគ្នានៃបំណែកនោះទេ ប្រវែងមួយក្នុងចំណោមប្រវែងរបស់ cuboid នឹងក្លាយជាគុណទូទៅនៃយ៉ាងហោចណាស់ 2 ប្រវែងនៃបំណែក ដោយសារវិធីសាស្រ្តទីបី និងទីបួន។ ការពិតនេះអាចត្រូវបានប្រើដើម្បីកំណត់ថាតើ cuboids ជាក់លាក់អាចត្រូវបានបង្កើតឡើងពីបំណែកដែលមិនមែនជា harmonic ដែរឬទេ។
សំណួរមួយចំនួនដើម្បីពិនិត្យមើលអ្វីដែលយើងបានរុករក:
តើ 2×4×12 បំណែកអាចបង្កើតជាគូបទំហំ 4×8×36 បានទេ? ចុះគូបដែលមានទំហំ 10×10×12 វិញ ?
ចាប់តាំងពី 4 / 2 = 2, 8 / 4 = 2 និង 36 / 12 = 3 គូប 4×8×36 អាចត្រូវបានបង្កើត។
ប្រវែងមួយនៃគូប 10×10×12 ត្រូវបានបែងចែកដោយ 12 ។ ប្រវែងផ្សេងទៀតគឺ 10 និង 10 ដែលមិនអាចបែងចែកដោយ 4 បានទេ។ ដូច្នេះ ប្រវែងនៃគូប 10×10×12 មិនមែនជាគុណនៃប្រវែងរបស់បំណែកនោះទេ។ ចាប់តាំងពី 12 / 4 = 3 និង 4 / 2 = 2 បំណែកនេះគឺអាម៉ូនិក ដូច្នេះគូប 10×10×12 មិនអាចបង្កើតឡើងពីបំណែកដែលមានទំហំ 2×4×12 បានទេ។
តើបំណែកទំហំ 1×3×5 អាចបង្កើតជាគូបទំហំ 2×15×8 បានទេ? ចុះគូប 3×9×14 វិញ?
ចាប់តាំងពី 5 មិនអាចបែងចែកដោយ 3 ដុំនេះមិនមែនជា harmonic ទេ។ យើងមិនអាចអនុវត្តចំណេះដឹងរបស់យើងអំពីបំណែក harmonic បានទេ។
វាអាចបង្កើតបានជាគូប 2×15×8 ជាមួយបំណែកទាំងនេះ។ បំណែក 1×3×5 ចំនួនបីអាចបង្កើតជារូបរាង 1×3×15 (ឬ 1×15×3) ហើយ 5 បំណែកដែលរៀបចំខុសគ្នាអាចបង្កើតជារាង 1×15×5 ។ រាងទាំងពីរនេះអាចត្រូវបានប្រើដើម្បីបង្កើតគូប 1×15×8 ដែលពីរអាចបង្កើតជាគូប 2×15×8 ។ យើងអាចប្រើប្រាស់ប្រតិបត្តិការដែលយើងបានពិភាក្សាឱ្យកាន់តែសង្ខេប៖ (1, 3, 5) → (1, 3 + 5, LCM(3,5)) = (1, 8, 15) → (2, 8, 15) → (2, 15, 8) ។
នៅពេលណាដែល 1×3×5 បំណែកត្រូវបានរួមបញ្ចូលគ្នា ចំនួនសរុបនៃគូបគឺជាគុណនៃ 5 ។ ចាប់តាំងពី 3 × 9 × 14 មិនអាចបែងចែកដោយ 5 គូប 3×9×14 មិនអាចបង្កើតបានពីបំណែកនៃទំហំ 1×3×5 បានទេ។
សេចក្តីសង្ខេបនៃច្បាប់សម្រាប់បំណែក harmonic និង non-harmonic
នេះគឺជាទិដ្ឋភាពទូទៅនៃអ្វីដែលយើងបានរៀន:
- ប្រសិនបើប្រវែងរបស់ cuboid គឺជាគុណនៃប្រវែងរបស់បំណែកមួយ នោះវាអាចត្រូវបានបង្កើតឡើងពីច្បាប់ចម្លងនៃបំណែកនោះ ដោយមិនគិតពីថាតើបំណែកនោះមានអារម្មណ៍ឬអត់។ cuboids បែបនេះអាចត្រូវបានបង្កើតឡើងជាមួយនឹងបំណែកទាំងអស់នៅក្នុងទិសដៅដូចគ្នា ប៉ុន្តែក៏អាចមានការរៀបចំដែលបំណែកមានទិសដៅខុសគ្នាផងដែរ។
- ប្រសិនបើបំណែកមួយគឺ harmonic នោះ cuboid ណាមួយដែលបានបង្កើតឡើងត្រូវតែមានប្រវែងដែលជាគុណនៃប្រវែងរបស់បំណែក។ ជាលទ្ធផល cuboid ណាមួយដែលបង្កើតឡើងពីបំណែក harmonic អាចមានបំណែកទាំងអស់នៅក្នុងទិសដៅដូចគ្នា ទោះបីជាវាមិនចាំបាច់ក៏ដោយ។
- ប្រសិនបើបំណែកមួយមិនមែនជា harmonic, មាន cuboids មួយចំនួនដែលអាចត្រូវបានបង្កើតឡើងប្រវែងដែលមិនមែនជាគុណនៃប្រវែងរបស់បំណែក (សូមមើលប្រតិបត្តិការទីបីនិងទីបួន). ក្នុងករណីនេះ បំណែកទាំងអស់មិនអាចមានទិសដៅដូចគ្នាបានទេ។ ដោយប្រើបំណែកដែលមិនមែនជា harmonic មនុស្សម្នាក់អាចបង្កើត cuboids នៃរាងផ្សេងៗគ្នាដោយប្រើវិធីសាស្រ្ត 4 ដែលបានរៀបរាប់ពីមុន។
តើការសង្កេតទាំងនេះមានប្រសិទ្ធភាពតែក្នុងបីវិមាត្រប៉ុណ្ណោះទេ?
ទេ. នៅក្នុងបរិបទនេះ មិនមានអ្វីពិសេសអំពី 3 វិមាត្រទេ។ តាមពិត ការកំណត់ប្រវែងមួយស្មើនឹង 1 គឺស្មើនឹងការកាត់បន្ថយបញ្ហាមកត្រឹម 2 វិមាត្រ។ លទ្ធផលក៏មានប្រសិទ្ធភាពលើសពី 3 វិមាត្រផងដែរ។ ឧទាហរណ៍ បំណែក 1×3×12×24 គឺ harmonic ។ ដូច្នេះ គូប 4 វិមាត្រណាមួយដែលបង្កើតឡើងពីបំណែក 4 វិមាត្រទាំងនេះត្រូវតែមានវិមាត្រ A, B × 3, C × 12 និង D × 24 សម្រាប់ចំនួនគត់វិជ្ជមានមួយចំនួន A, B, C និង D ។
តើធ្វើដូចម្តេចដើម្បីទទួលបានល្បែងផ្គុំរូបដោយដៃ?
យើងមិនអាចប្រាប់អ្នកពីរបៀបធ្វើបំណែក 4 វិមាត្របានទេ:) ប៉ុន្តែនៅក្នុង 3-dimensions ប្រសិនបើអ្នកមានគ្រាប់ឡាក់ទំនេរជាច្រើន, you can tape them together to form pieces.
ជំនួសឱ្យប្រអប់ 5×5×5 មួយអាចប្រើ, ឧទាហរណ៍, ប្រអប់ស្បែកជើង. ប្រសិនបើមួយកាន់វាអង្កត់ទ្រូង, បំណែកនឹងស្ថិតនៅកន្លែងដែលពួកគេត្រូវបានដាក់.
ល្បែងផ្គុំរូបមួយចំនួនមានកម្ពស់ 1 (ឧទាហរណ៍ "1×7×10 1") ដូច្នេះហើយជាល្បែងផ្គុំរូប 2 វិមាត្រ។ មួយអាចកាត់ចតុកោណកែងពីក្រដាសក្រាហ្វដើម្បីប្រើជាបំណែកសម្រាប់ល្បែងផ្គុំរូបទាំងនេះ.
ការទទួលស្គាល់
ចំណាប់អារម្មណ៍របស់យើងក្នុងការវេចខ្ចប់ល្បែងផ្គុំរូបត្រូវបានបញ្ឆេះនៅពេលឃើញកំណែឈើនៃរូបផ្គុំរូប "5x5x5 1" នៅឯការតាំងពិព័រណ៍គណិតវិទ្យា។ បន្ទាប់ពីឯកសារយោងទៅអ្នកនិពន្ធរបស់វា, គណិតវិទូល្បីល្បាញលោក John Horton Conway, យើងបានរកឃើញល្បែងផ្គុំរូប "3x3x3 2", "5x5x5 2", និង "5x5x5 3" ពីគាត់.
ផ្នែក "វេចខ្ចប់ជាមួយតែមួយប្រភេទនៃបំណែក" ត្រូវបានបំផុសគំនិតដោយការងាររបស់គណិតវិទូហូឡង់ de Bruijn. ដើម្បីស្វែងយល់បន្ថែមអំពីការសង្កេតរបស់ de Bruijn លើការវេចខ្ចប់បំណែករាងចតុកោណ សូមពិគ្រោះជាមួយអត្ថបទនេះ។ អ្នកអាចអានភស្តុតាងរបស់ de Bruijn នៃលក្ខណៈសម្បត្តិនៃបំណែកអាម៉ូនិកនៅទីនេះ.
Follow ឬ subscribe សម្រាប់ updates: