300000
English | Français | فارسی | 中文 | Українська | Azerbaijani | ខ្មែរ | Tiếng Việt | Bahasa Melayu | Deutsch | O'zbek | РусскийPile-Poil©
Nombre de fois que ce casse-tête a été résolu/essayé : 6980/11160
Pourquoi devrais-je lire cette « Matière à réflexion » ?
Parce que vous serez surpris.
Après avoir essayé quelques puzzles d’emballage, quel domaine des mathématiques pensez-vous être le plus utile pour les résoudre :
1) Algèbre, 2) Théorie des probabilités, 3) Géométrie, 4) Théorie des nombres, 5) Symétries, 6) Un autre domaine ?
Ce qui s’avère le plus utile, c’est de penser à la divisibilité des nombres, en particulier la divisibilité par 2. C’est un sujet de la théorie des nombres. Les choses que nous empilons sont des objets géométriques, mais cela ne signifie pas que des connaissances géométriques sont nécessaires pour résoudre les énigmes. D’après la géométrie, nous avons besoin de savoir quelle est l’aire d’un carré ou d’un rectangle, mais rien de plus.
Pour certaines énigmes, il est également très utile de penser à la symétrie.
Astuces rapides
Ce sont des conseils pour ceux qui cherchent de l’aide mais qui ne sont pas intéressés par le contexte mathématique.
- En regardant les numéros à côté de « Ce puzzle a gagné/joué » pour chaque puzzle, vérifiez lesquels sont les plus faciles. Commencer par les énigmes les plus simples est toujours une bonne idée, et vous vous entraînerez à manipuler l’interface.
- Les énigmes « 2×3×3 1 » et « 2×3×3 2 » sont facilement résolues par essais et erreurs.
- Si votre premier essai sur le puzzle « 1×7×10 1 » n’est pas réussi, faites pivoter les pièces lors de votre prochain essai.
- « 1×7×7 1 » est un puzzle où la réflexion sur la symétrie aide. La raison en est que le récipient (grille) a une base carrée avec 4 côtés de même longueur, et nous avons 4 longues pièces de la même forme. Il faut donc les mettre symétriquement. Il n’y a qu’une seule pièce de forme carrée violette. Pour avoir une solution à symétrie de rotation de 90°, cette pièce doit se trouver au milieu. N’importe quel autre endroit briserait la symétrie à 90° de la solution.
- Les puzzles avec des boutons plus sombres nécessitent plus de réflexion. Commencez par bien comprendre le puzzle « 3×3×3 2 » avant de passer aux puzzles 5×5×5.
Comment peut-on résoudre ces énigmes sans essais et erreurs ?
Voici quelques conseils :
- Divisez un problème difficile en problèmes plus faciles, c’est-à-dire en sous-objectifs. Par exemple, pour remplir tout le conteneur, il faut remplir chaque couche.
- Disposez les pièces de manière symétrique, surtout si le récipient est symétrique comme un cube 3×3×3 ou le récipient de forme carrée 1×7×7.
- Tirez le meilleur parti des informations fournies. Quelles sont les tailles des pièces ? Combien d’entre eux ont la même forme ?
Le reste de cette « Matière à réflexion » a pour but de résoudre toutes les énigmes sans essais ni erreurs, en proposant plutôt des questions simples et en y répondant.
Définitions
Pour plus de clarté, voici quelques termes que nous utiliserons pour discuter des problèmes d’emballage :
Morceau
L’une des formes qui seront assemblées pour former le plus grand solide.
Une pièce impaire est une pièce dont les longueurs sont toutes impaires, comme une pièce 1×1×1 ou une pièce 1×3×5.
Une pièce est paire si elle a au moins deux longueurs paires, comme 1×2×4 ou 2×2×2.
Toutes les pièces sont-elles paires ou impaires ?
NON. Une pièce avec exactement une longueur égale, telle que 1×2×3, ne correspond à aucune des deux définitions. Dans les sections suivantes, nous nous concentrerons sur les pièces paires et impaires.
Cuboïde/Conteneur
Un cuboïde est un prisme rectangulaire. Nous utilisons le mot « conteneur » pour désigner la coquille vide du cuboïde. Nous appelons « cuboïde » le contenu du contenant. Un récipient doit être rempli de morceaux et un cuboïde est créé à partir de morceaux.
Couche
Une couche est une tranche d’épaisseur 1 dans une direction parallèle à une face du récipient. Un récipient 3×4×5 a 3 couches de taille 4×5, 4 couches de taille 3×5 et 5 couches de taille 3×4.
Combien de couches comporte un conteneur 1×5×7 ?
Il a une couche 5×7, cinq couches 1×7 et sept couches 1×5. Au total, il a 1 + 5 + 7 = 13 couches.
Cube
Plus précisément, un cube 1×1×1, pas un cube plus grand. Une pièce 1×1×1 se compose de 1 cube, tandis qu’une pièce 1×1×3 se compose de 1 × 1 & times 3 = 3 cubes.
Cube
Quelques pièces attachées les unes aux autres forment un bloc de construction. Les blocs de construction intéressants auront une symétrie. Pour les puzzles plus difficiles, plusieurs blocs de construction identiques ou identiques à un miroir ainsi qu’une pièce centrale rempliront le récipient.
Stratégie
La moitié de la solution d’un problème difficile consiste à diviser le problème difficile en problèmes plus petits.
Pour ce faire, il faut se poser des questions simples. Les questions suivantes seront utiles pour résoudre les énigmes d’emballage.
Chaque cuboïde peut-il être formé avec des morceaux de taille 1×2×2 ? Par exemple, peut-on former un cuboïde 3×3×3 en utilisant uniquement des morceaux de taille 1×2×2 ?
NON. Une pièce 1×2×2 se compose d’un nombre pair de cubes. Par conséquent, n’importe quel nombre de pièces 1×2×2 aura ensemble un nombre total pair de cubes. Étant donné qu’un cuboïde 3×3×3 est constitué d’un nombre impair de cubes, il ne peut pas être formé de cette manière.
Dans les prochaines sections, nous explorerons comment la divisibilité, en particulier par 2, détermine comment les pièces doivent être placées pour résoudre certaines énigmes.
Les pièces 1×2×2 peuvent-elles au moins remplir n’importe quelle couche du récipient 3×3×3 ?
La réponse est encore une fois NON. L’aire d’une couche qui peut être occupée par une pièce est l’aire de l’une des faces de l’œuvre, n’est-ce pas ?
Quels sont les visages d’une pièce 1×2×2 ?
Une pièce 1×2×2 a deux paires de faces 1×2 parallèles, et une paire de faces 2×2.
Quelles sont les aires de ces visages et qu’ont-elles en commun ?
Les aires sont 1 & fois 2 = 2 et 2 & fois 2 = 4. 2 et 4 sont tous deux des nombres pairs.
On observe qu’une pièce de 1×2×2 ne peut occuper qu’un nombre pair de cubes (2 ou 4) dans chaque couche.
Est-ce vrai pour toutes les pièces paires ?
Chaque face d’une pièce a deux longueurs. Étant donné que les pièces paires ont au plus une longueur impaire, chacune de leurs faces aura au moins une longueur paire. Parce que pair & fois impair = pair, l’aire de chaque face sera paire. C’est pourquoi nous les appelons pièces égales !
Nous avons appris que les cuboïdes avec des longueurs de côté impaires ne peuvent pas être formés à partir de morceaux pairs. Une couche avec une zone impaire ne peut pas non plus être remplie de morceaux pairs. Par conséquent, le puzzle « 3×3×3 2 » comporte quelques pièces 1×1×1, qui sont des pièces impaires.
Voici une autre question utile à considérer :
L’un des deux types de pièces (1×1×1 et 1×2×2) est-il plus « précieux » que l’autre ?
OUI. Si nous n’avions que 1×1×1 pièces, alors n’importe quel puzzle serait trivial, êtes-vous d’accord ? Si nous n’avions que 1×2×2 pièces, alors un conteneur impair ne pourrait pas être rempli, comme indiqué ci-dessus.
La question évidente est la suivante : quel est le nombre minimum de pièces 1×1×1 qui peuvent remplir le conteneur 3×3×3 ?
Naturellement, les questions suivantes se posent :
Pourquoi trois pièces 1×1×1 suffisent-elles ?
Pour répondre à cette question, nous allons comparer le nombre de couches impaires (couches avec une zone impaire) au nombre de couches de zones impaires qui peuvent être remplies avec des pièces paires et seulement 3 cubes.
Combien de couches comporte un conteneur 3×3×3 ?
Dans chacune des trois directions (largeur, hauteur, profondeur), le conteneur comporte 3 couches. Il y a 3 + 3 + 3 = 9 couches impaires qui sont remplies lorsque le conteneur est rempli.
Combien de couches impaires de 3×3 peuvent être complétées avec une seule pièce de 1×1×1 (et même de 1×2×2 pièces) ?
Trois couches : la couche horizontale et les deux couches verticales qui contiennent la pièce 1×1×1. Par conséquent, 3 cubes peuvent aider à remplir au maximum 3 & fois 3 = 9 couches.
Cela montre que 3 cubes sont nécessaires, et parce que le puzzle « 3×3×2 2 » est résolvable, 3 cubes sont également suffisants pour remplir les 9 couches impaires.
Qu’est-ce que cela nous dit sur l’emplacement des 3 cubes dans le
Puzzle « 3×3×3 2 » ?
Dans chacune des 9 couches, il ne peut y avoir qu'1 cube, pas 0 cube et pas 2 cubes ! Sinon, 3 cubes ne suffiraient pas pour les 9 couches.
Il s’agit d’une percée pour la solution. De plus, la seule façon de placer les cubes est le long d’une diagonale - avec un cube au centre et les deux autres cubes dans des coins diagonaux opposés. Sinon, les pièces encombrantes 1×2×2 seraient trop grandes pour remplir l’espace autour des 3 cubes.
Par conséquent, placez un cube dans un coin, et trois pièces 1×2×2 de manière symétrique autour de ce cube. Mettez un cube au centre, un dans le coin opposé, et le reste sera évident.
Que pouvons-nous apprendre d’autre de cette solution ? Par exemple, a-t-il des symétries ?
Les symétries sont visibles après avoir placé le premier cube dans le coin et les trois pièces 1×2×2 autour de lui. La solution a une symétrie de rotation de 120° avec la diagonale du cube comme axe de rotation (120° = 1/3 de la rotation du cercle complet).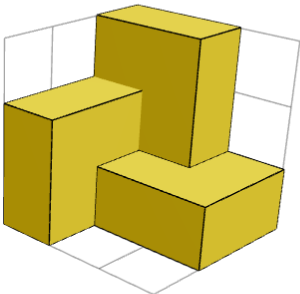
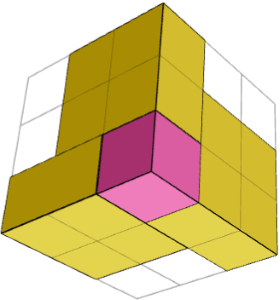
La solution est-elle la somme de blocs de construction identiques ou symétriques, chacun composé de plusieurs pièces ?
OUI. Le cuboïde est la somme de 2 blocs de construction symétriques en miroir (1 cube dans un coin + trois pièces 1×2×2 autour de lui) et d’un cube au milieu. Les 2 images ci-dessus montrent un bloc de construction de 2 côtés.
Existe-t-il une autre façon de résoudre ce puzzle en utilisant différents blocs de construction ?
OUI. Les images de gauche et de droite ci-dessous montrent deux blocs de construction symétriques en miroir pour le puzzle « 3×3×3 2 ». Ils peuvent être combinés avec un cube central (image du milieu) pour résoudre le puzzle.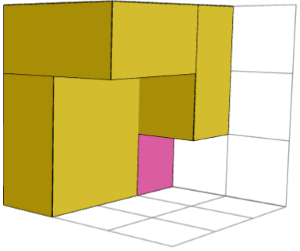
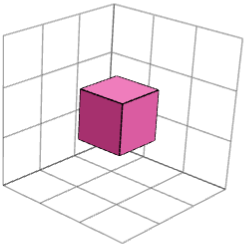
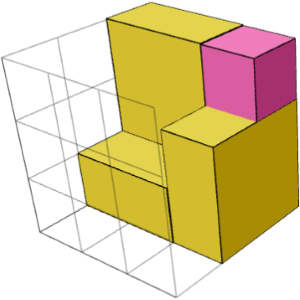
Pourquoi devrions-nous nous donner la peine de penser à des blocs de construction ?
Il est plus facile d’utiliser un petit nombre donné de pièces et de créer quelque chose de symétrique à partir d’elles, que de remplir le plus grand récipient avec toutes les pièces.
Les blocs de construction peuvent-ils être utilisés pour résoudre des énigmes plus grandes, telles que « 3×5×7 1 » ?
OUI. Les conteneurs plus grands, même si leurs longueurs sont toutes différentes, peuvent être remplis à l’aide de blocs de construction identiques/symétriques en miroir. Il existe plusieurs façons de résoudre le puzzle « 3×5×7 1 » à l’aide de blocs de construction et d’une pièce centrale impaire. Nous vous laissons le soin de trouver quelques exemples.
Comment savoir quelles pièces doivent constituer un bloc de construction ?
Pensons d’abord au centre d’un cuboïde étrange. Parce que la position centrale est unique, si nous voulons une solution symétrique, le centre doit être occupé par une pièce de la même forme que le contenant. Le cuboïde 3×3×3 est un cube, donc la pièce maîtresse doit être un cube. Une pièce de 1×2×2 au centre briserait la symétrie.
Cela signifie que nous avons 6 pièces jaunes et 3 − 1 = 2 pièces roses pour construire un certain nombre de blocs de construction identiques.
Combien de blocs de construction devrions-nous essayer de créer ?
Les blocs de construction doivent former le cuboïde moins la pièce centrale. Par conséquent, le nombre de pièces jaunes dans un bloc de construction doit être un diviseur de 6 (le nombre total de blocs jaunes) et le nombre de pièces roses d’un bloc de construction doit être divisé par 2 (le nombre de cubes roses restants après en avoir réservé un pour le centre).
Ainsi, le nombre N de blocs de construction identiques est le plus grand diviseur commun du nombre de pièces identiques, ici 6 et 2, qui est PGCD(6,2) = 2. Nous devons donc créer un bloc de construction à partir de 2 / 2 = 1 cube rose et 6 / 2 = 3 blocs jaunes. C’est ce que nous avons fait.
Résumez l’algorithme mathématique pour l’utiliser pour des puzzles plus importants.
Pour un conteneur impair :
- Alignez les pièces étranges pour vous assurer qu’elles ne se chevauchent dans aucune couche. Ils doivent relier un coin du récipient avec le coin opposé du récipient. Si les pièces impaires sont des cubes, elles forment une diagonale. Si les pièces impaires sont plus grandes (1x1x3), elles forment une diagonale non droite.
- S’il n’y a qu’un seul type de pièce uniforme, utilisez-les pour remplir le récipient.
- S’il existe différents types de pièces paires :
- Mettez de côté la pièce centrale impaire. À partir des morceaux restants, déterminez le plus grand diviseur commun N du nombre de morceaux des différents types. N est le nombre de blocs de construction.
- Créez N blocs de construction identiques et assemblez-les avec la pièce centrale en cas de conteneur étrange.
Bien que les petites énigmes puissent être facilement résolues par essais et erreurs, cette stratégie ne fonctionne pas pour les grandes énigmes. Notre exploration des pièces paires et impaires révèle une raison importante : le placement des pièces impaires est crucial, car il y a très peu de façons de les placer correctement. En utilisant des essais et des erreurs, on peut faire une erreur dès le début et ne se rendre compte que quelque chose s’est mal passé qu’après avoir placé de nombreuses pièces. Il est donc incroyablement difficile de déterminer la cause de l’erreur, de sorte qu’il n’y a pas de retour d’information utilisable ; La méthode d’essai et d’erreur n’est pas efficace pour les grands conteneurs. Il faut réfléchir.
Emballage avec un seul type de pièce
Dans cette section, nous allons explorer les tailles des cuboïdes qui peuvent être formés à partir d’un seul type de pièce. Il s’agit d’une section théorique, non nécessaire pour résoudre les énigmes ci-dessus. Cette section ne nécessite pas de calculs difficiles.
Avec suffisamment de pièces 1×1×1, nous pouvons facilement former un cuboïde de n’importe quelle taille. Mais qu’en est-il des autres pièces, telles que les pièces 2×3×4 ou 1×2×5 ? Il y a deux questions principales à investiguer. Tout d’abord, étant donné les longueurs d’une pièce et les longueurs d’un cuboïde, comment pouvons-nous déterminer si le cuboïde peut être créé à partir de copies de l’œuvre ? Deuxièmement, comment pouvons-nous, à partir d’une seule pièce, générer les longueurs d’un cuboïde qui peut être formé ? Tout au long de cette section, nous examinerons des questions plus simples tout en explorant ces deux problèmes importants.
Un cuboïde 2×6×10 peut-il être formé à partir de seulement 1×2×5 pièces ?
OUI! Trois pièces 1×2×5 peuvent être placées côte à côte pour former une forme 1×6×5 (3 × 2 = 6). Nous pouvons ensuite créer une deuxième forme 1×6×5 et les combiner en une forme 1×6×10. Enfin, deux formes 1×6×10 peuvent être placées ensemble pour former un cuboïde 2×6×10.
Est-il possible de former un cuboïde 10×12×14 en utilisant uniquement des morceaux de taille 2×5×6 ?
Indice
Il n’est pas nécessaire d’imaginer comment les pièces seraient disposées.
Un autre indice ?
Une pièce 2×5×6 est la même chose qu’une pièce 5×6×2 car elle peut être tournée.
Répondre
OUI. Étant donné que 10 / 5 = 2, 12 / 6 = 2 et 14 / 2 = 7, le plus grand cuboïde peut être considéré comme un arrangement 2×2×7 des pièces 5×6×2. Les pièces 5×6×2 peuvent toutes être placées avec la même orientation.
Comment pouvons-nous généraliser ces résultats ?
Supposons que nous n’ayons que des morceaux de taille x & fois y & fois z. Ensuite, la construction d’un cuboïde X & fois Y & fois Z est possible s’il existe des entiers positifs A, B, C tels que Ax, By et Cz sont égaux à X, Y et Z dans un certain ordre.
Combien de pièces seront utilisées dans ce cas ?
Nous pouvons disposer les pièces A dans une direction, B dans une autre et C dans une troisième direction. Au total, des pièces A & times B & times C seront utilisées.
Pourquoi Ax, By et Cz peuvent-ils être égaux à X, Y et Z dans n’importe quel ordre ?
Un conteneur de taille X & fois Y & fois Z est la même chose qu’un cuboïde Z & fois X & fois Y . L’ordre des longueurs n’a pas d’importance car le cuboïde peut être tourné.
Est-il vrai que tout cuboïde formé de morceaux de 1&fois2&fois3 doit avoir des longueurs A, B & fois 2, C & fois 3, pour des entiers positifs A, B, C ?
NON. Si toutes les pièces 1×2×3 sont orientées dans la même direction, le cuboïde aura la taille A & fois (B & fois 2) & fois (C & fois 3). Mais les pièces peuvent être orientées différemment et former un cuboïde. Par exemple, les pièces 1×2×3 peuvent former un cuboïde 1×5×6, même si 1, 5 et 6 ne sont pas égaux à A, B & fois 2 et C & fois 3 dans n’importe quel ordre. Un autre exemple est le puzzle « 1×7×10 1 », qui est composé de 1×2×5 pièces.
Quelle est la relation entre les longueurs de la pièce et les longueurs du cuboïde dans ces deux exemples ?
Dans ces deux exemples, l’une des longueurs du cuboïde est la somme de deux des longueurs de la pièce. Une longueur différente du cuboïde est le PPCM (plus petit commun multiple) des deux mêmes longueurs de la pièce. Dans le cas du cuboïde 1×5×6 formé de 1×2×3 pièces, nous avons 1×5×6 = 1× (2 + 3) × LCM(2,3). De même, 1×7×10 = 1 & fois (2 + 5) & fois LCM(2,5).
Comment pouvons-nous utiliser ce fait pour trouver un moyen de générer les longueurs de cuboïdes qui peuvent être construits à partir d’une pièce donnée ?
Nous commençons par représenter la longueur d’une pièce sous la forme d’un triplet ordonné. Par exemple, une pièce 1×2×3 est représentée par (1, 2, 3). Maintenant, il y a 3 opérations que nous pouvons effectuer à plusieurs reprises pour donner les longueurs de cuboïdes qui peuvent être formées à partir de cette pièce. Il s’agit de :
- Modifiez l’ordre des longueurs. C’est ce qu’on appelle une permutation. Dans notre cas, il représente une rotation dans l’espace à 3 dimensions. Un exemple est
(1, 2, 3) → (2, 3, 1). - Multipliez les longueurs par les entiers positifs A, B et C, respectivement. Cela correspond à la formation d’un cuboïde plus grand en plaçant des morceaux A dans une direction, B dans une autre direction et C dans la troisième direction. Par exemple, nous pouvons multiplier par 1, 4 et 3 pour donner (1, 2, 3) → (1 & fois 1, 4 & fois 2, 3 & fois 3) = (1, 8, 9).
- Prenez deux longueurs et remplacez-les une par leur somme et l’autre par leur PPCM. Cela correspond à la formation d’un cuboïde plus grand avec des pièces orientées dans différentes directions. Par exemple, en choisissant les longueurs 2 et 3, nous obtiendrions (1, 2, 3) → (1, 2 + 3, LCM(2,3)) = (1, 5, 6).
Peut-on combiner les morceaux d’une 4ème manière pour produire un cuboïde dont la forme est différente du résultat de la 3ème opération ?
OUI. Considérons un morceau de taille x & fois y & fois z. La troisième opération produit un cuboïde de taille x × (y + z) & fois LCM(y,z), où une longueur x est inchangée entre la pièce et le cuboïde.
Une méthode similaire mais différente serait de mettre à nouveau LCM(y,z)/y plusieurs pièces l’une à côté de l’autre et LCM(y,z)/y plusieurs pièces l’une à côté de l’autre, comme auparavant, mais maintenant de faire pivoter un ensemble de 90° de sorte que les deux blocs aient la même longueur LCM(y,z), mais des hauteurs différentes. En termes mathématiques, nous n’attachons pas x & fois y & fois LCM(y,z) et x & fois z & fois LCM(y,z) pour former x & fois (y + z) & fois LCM(y,z). Au lieu de cela, l’un d’entre eux, disons x & fois z & fois LCM(y,z), est tourné vers z & fois x & fois LCM(y,z) puis attaché.
L’aire de base rectangulaire n’est alors pas (y + z) & fois LCM(y,z), mais plutôt (x + z) & fois LCM(y,z). Ensuite, les deux blocs de construction x & fois y & fois LCM(y,z) et z & fois x & fois LCM(y,z) ont respectivement les longueurs x et z dans la direction X.
En empilant LCM(x,z)/x de nombreux blocs de construction de hauteur x et LCM(x,z)/z de nombreux blocs de construction de hauteur z, les deux piles atteignent la hauteur LCM(x,z). Lorsqu’ils sont fixés, le résultat est un cuboïde de taille LCM(x,z) & fois (x + z) & fois LCM(y,z), qui a une forme et une taille différentes de celles de n’importe quel cuboïde résultant de la troisième opération.
On peut répéter ces opérations dans n’importe quel ordre, en générant d’abord un cuboïde à partir d’un morceau, puis en utilisant le cuboïde comme un « morceau » pour générer un cuboïde encore plus grand. Nous avons vu plus tôt comment un cuboïde 2×6×10 peut être formé à partir de pièces 1×2×5. Dans ce cas, une seule opération est nécessaire, multipliée par 2, 3 et 2, respectivement : (1, 2, 5) → (2 & fois 1, 3 & fois 2, 2 & fois 5) = (2, 5, 10).
Ainsi, les morceaux de taille x & fois y & fois z peuvent non seulement construire des cuboïdes de taille Ax & fois By × Cz mais, par exemple, aussi de taille x × (y + z) × LCM(y,z), où LCM(y,z) est le plus petit commun multiple de y et z. En rassemblant plusieurs de ces éléments constitutifs, on obtient des cuboïdes de taille Ax × B(y + z) + C(LCM(y,z)).
Nous allons maintenant examiner un type particulier de pièce. Un morceau est harmonique si chacune de ses plus grandes longueurs est divisible par la suivante plus petite. Par exemple, un morceau 1×2×6 est harmonique puisque 2 / 1 = 1 et 6 / 2 = 3. Une pièce 1×4×6 n’est pas harmonique puisque 6 n’est pas un multiple de 4.
Est-ce qu’une pièce 1×2×3 est harmonique ?
NON, car 3 n’est pas divisible par 2.
Qu’est-ce qui rend les pièces harmoniques spéciales dans l’emballage ? Comment se rapportent-ils à notre discussion sur la longueur des morceaux et des cuboïdes ?
Nous avons déjà observé que n’importe quelle pièce peut former un cuboïde dont les longueurs sont des multiples des longueurs de la pièce. Il s’avère que les longueurs de tout cuboïde formé de morceaux harmoniques identiques doivent être des multiples des longueurs des morceaux. C’est-à-dire que si une pièce harmonique a des longueurs x, y et z, tout cuboïde formé à partir de copies de cette pièce doit avoir une longueur divisible par x, une autre divisible par y et la troisième divisible par z. Bien qu’il s’agisse d’une simple affirmation, la preuve nécessite des concepts qui dépassent le cadre de ce site Web. Un lien vers la preuve se trouve dans la section « Remerciements ».
En quoi ce fait est-il cohérent avec les quatre opérations que nous avons discutées ci-dessus ?
Nous pouvons commencer par penser à une pièce comme à un cuboïde formé à partir d’une copie de la pièce. Une pièce x × y × z est aussi un cuboïde x × y & times z . Les longueurs de ce cuboïde sont des multiples des longueurs de la pièce, puisque chaque nombre est un multiple de lui-même. Nous allons montrer pourquoi les quatre méthodes que nous avons introduites produisent des cuboïdes dont les longueurs sont encore des multiples des longueurs de la pièce.
- Changer l’ordre des longueurs (permutation) : il s’agit simplement d’une rotation, et ne change pas réellement les longueurs du cuboïde. Les longueurs du cuboïde seront toujours des multiples de la longueur de la pièce.
- Multiplier les longueurs du cuboïde par des entiers positifs : si les longueurs du cuboïde sont déjà des multiples de la longueur de la pièce, cela ne changera pas. Ils deviendront simplement des multiples plus grands. Si X = Ax est un multiple de x, alors DX = DAx est également un multiple de x, pour tout entier positif D.
- Remplacer deux longueurs par leur somme et LCM : c’est pourquoi les pièces harmoniques sont importantes ; Nous devrons utiliser la définition des pièces harmoniques. Supposons que nous commencions par une pièce harmonique (x, y, z), à partir de laquelle nous avons déjà formé le cuboïde (Ax, By, Cz). L’ordre des longueurs n’a pas d’importance puisque le cuboïde peut être tourné. Nous allons maintenant effectuer la troisième opération sur deux longueurs quelconques du cuboïde, disons Ax et By : (Ax, By, Cz) → (Ax + By, LCM(Ax,By), Cz). Or, puisque la pièce (x, y, z) est harmonique, l’une des deux longueurs x et y est un multiple de l’autre. Supposons que y est un multiple de x. Par conséquent, By est également un multiple de x, et puisque Ax l’est également, la somme Ax + By est un multiple de x. Ensuite, LCM(Ax,By) est le plus petit commun multiple de Ax et By, il est donc par définition un multiple de By, donc il est divisible par y. Enfin, Cz est, bien sûr, un multiple de z. Par conséquent, les longueurs du nouveau cuboïde (Ax + By, LCM(Ax,By), Cz) sont toujours des multiples des longueurs de la pièce.
- Qu’en est-il de la quatrième opération ? Comme cette opération est similaire à la troisième, l’argument présenté ci-dessus peut être adapté à ce cas. Nous le laissons comme un exercice.
Nous avons montré que les quatre opérations, exécutées de manière répétée dans n’importe quel ordre sur n’importe quelle pièce harmonique, aboutiront à un cuboïde dont les longueurs sont des multiples des longueurs de la pièce. Il est important de noter que dans notre discussion de la troisième opération (et de la quatrième !), nous misons sur le fait que la pièce est harmonique. Lorsqu’un morceau n’est pas harmonique, l’argument échoue. C’est la principale différence entre les pièces harmoniques et non harmoniques. Pour les pièces harmoniques, les troisième et quatrième méthodes ne produisent pas de formes supplémentaires par rapport aux deux premières méthodes.
En conséquence, tout cuboïde formé de pièces harmoniques peut avoir toutes les pièces dans la même orientation. Par conséquent, si nous essayons de former un cuboïde à partir de morceaux harmoniques identiques, il suffit d’essayer de les disposer tous orientés dans la même direction. Si cela n’est pas possible, le cuboïde ne peut pas être formé du tout.
Comme un morceau 1×2×2 est harmonique, tout cuboïde formé à partir de copies de ce morceau doit avoir des longueurs A, B & fois 2, et C & fois 2 pour certains entiers A, B et C. L’image ci-dessous montre un cuboïde 5×4×4 formé de 1×2×2 pièces, qui ont toutes la même orientation.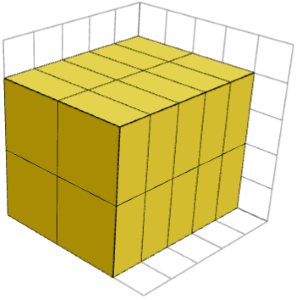
Quelles sont les valeurs de A, B et C ?
En posant A, B & fois 2 et C & fois 2 égaux à 5, 4 et 4, respectivement, nous trouvons A = 5 / 1 = 1, B = 4 / 2 = 2 et C = 4 / 2 = 2.
Lors de l’emballage avec des morceaux harmoniques, les morceaux doivent-ils être orientés dans la même direction ?
NON! Bien qu’il soit toujours possible pour toutes les pièces d’avoir la même orientation, il peut y avoir d’autres arrangements, mais ils ne forment pas de nouvelles formes. L’image ci-dessous montre une façon différente de former un cuboïde 5×4×4 à partir de 1×2×2 pièc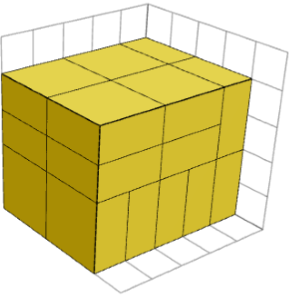es.
Quelles sont les règles pour les pièces non harmoniques ?
Lorsque l’on travaille avec une pièce non harmonique x & fois y & times z, il est possible de former des cuboïdes dont les tailles ne sont pas Ax × By × Cz pour tous les entiers A, B, C. Par exemple, un cuboïde 1×5×6 peut être créé à partir de pièces 1×2×3. C’est le résultat de la troisième opération, comme nous l’avons vu plus haut.
Il est important de noter que le nombre de cubes dans le cuboïde doit toujours être divisible par le nombre de cubes dans la pièce. Lorsque les longueurs du cube ne sont pas chacune un multiple d’une longueur différente de la pièce, l’une des longueurs du cuboïde sera un multiple commun d’au moins 2 longueurs de la pièce, en raison des troisième et quatrième méthodes. Ce fait peut être utilisé pour déterminer si certains cuboïdes peuvent être formés à partir de pièces non harmoniques.
Quelques questions pour revoir ce que nous avons exploré :
Est-ce que 2×4×12 pièces peuvent former un cuboïde de taille 4×8×36 ? Que diriez-vous d’un cuboïde de taille 10×10×12 ?
Comme 4 / 2 = 2, 8 / 4 = 2 et 36 / 12 = 3, un cuboïde 4×8×36 peut être formé.
L’une des longueurs d’un cuboïde 10×10×12 est divisible par 12. Les autres longueurs sont 10 et 10, dont aucune n’est divisible par 4. Par conséquent, les longueurs du cuboïde 10×10×12 ne sont pas des multiples des longueurs de la pièce. Puisque 12 / 4 = 3 et 4 / 2 = 2, la pièce est harmonique, donc un cuboïde 10×10×12 ne peut pas être formé à partir de morceaux de taille 2×4×12.
Des morceaux de taille 1×3×5 peuvent-ils former un cuboïde de taille 2×15×8 ? Qu’en est-il d’un cuboïde 3×9×14 ?
Comme 5 n’est pas divisible par 3, le morceau n’est pas harmonique. Nous ne pouvons pas appliquer nos connaissances sur les pièces harmoniques.
Il est possible de former un cuboïde 2×15×8 avec ces pièces. Trois pièces 1×3×5 peuvent former une forme 1×3×15 (ou 1×15×3), et 5 des pièces disposées différemment peuvent former une forme 1×15×5. Ces deux formes peuvent être utilisées pour créer un cuboïde 1×15×8, dont deux peuvent former un cuboïde 2×15×8. Nous pouvons utiliser les opérations que nous avons abordées pour être plus concis : (1, 3, 5) → (1, 3 + 5, LCM(3,5)) = (1, 8, 15) → (2, 8, 15) → (2, 15, 8).
Chaque fois que 1×3×5 pièces sont combinées, le nombre total de cubes est un multiple de 5. Étant donné que 3 & fois 9 & fois 14 n’est pas divisible par 5, un cuboïde 3×9×14 ne peut pas être créé à partir de morceaux de taille 1×3×5.
Résumé des règles pour les pièces harmoniques et non harmoniques
Voici un aperçu de ce que nous avons appris :
- Si les longueurs d’un cuboïde sont des multiples des longueurs d’un morceau, alors il peut être formé à partir de copies de ce morceau, que le morceau soit harmonique ou non. De tels cuboïdes peuvent être formés avec toutes les pièces dans la même orientation, mais il peut également exister des arrangements dans lesquels les pièces ont des orientations différentes.
- Si une pièce est harmonique, alors tout cuboïde formé doit avoir des longueurs qui sont des multiples des longueurs de la pièce. En conséquence, tout cuboïde formé de pièces harmoniques peut avoir toutes les pièces dans la même orientation, bien que cela ne soit pas toujours nécessaire.
- Si une pièce n’est pas harmonique, il y a des cuboïdes qui peuvent être formés dont les longueurs ne sont pas des multiples des longueurs de la pièce (voir les troisième et quatrième opérations). Dans ce cas, les pièces ne peuvent pas toutes avoir la même orientation. En utilisant des pièces non harmoniques, on peut créer des cuboïdes de différentes formes en utilisant les 4 méthodes décrites précédemment.
Ces observations ne sont-elles valables qu’en trois dimensions ?
NON. Dans ce contexte, il n’y a rien de spécial à propos des 3 dimensions. En fait, définir l’une des longueurs égale à 1 équivaut à réduire le problème à 2 dimensions. Les résultats sont également valables dans plus de 3 dimensions. Par exemple, un morceau 1×3×12×24 est harmonique. Par conséquent, tout cuboïde à 4 dimensions formé à partir de ces morceaux à 4 dimensions doit avoir les dimensions A, B & fois 3, C & fois 12 et D & fois 24 pour certains entiers positifs A, B, C et D.
Comment obtenir des puzzles pratiques ?
Nous ne pouvons pas vous dire comment fabriquer des pièces en 4 dimensions :) Mais en 3 dimensions, si vous avez beaucoup de dés de rechange, vous pouvez les coller ensemble pour former des pièces.
Au lieu d’une boîte 5×5×5, on pourrait utiliser, par exemple, une boîte à chaussures. Si on le tient en diagonale, les pièces resteront là où elles sont placées.
Certains puzzles ont une hauteur de 1 (par exemple, « 1×7×10 1 ») et sont donc des puzzles à 2 dimensions. On peut découper des rectangles dans du papier millimétré pour les utiliser comme pièces pour ces puzzles.
Reconnaissance
Notre intérêt pour l’emballage des puzzles a été ravivé lorsque nous avons vu la version en bois du puzzle « 5x5x5 1 » lors d’une exposition de mathématiques. En suivant la référence à son auteur, le célèbre mathématicien John Horton Conway, nous avons trouvé les puzzles « 3x3x3 2 », « 5x5x5 2 », et « 5x5x5 3 » de lui.
La section « Emballage avec un seul type de pièce » s’inspire des travaux du mathématicien néerlandais de Bruijn. Pour en savoir plus sur les observations de de Bruijn sur l’emballage des pièces rectangulaires, consultez cet article. Vous pouvez lire la preuve de de Bruijn des propriétés des pièces harmoniques ici.
Suivez ou abonnez-vous à l'Infolettre