Pembungkusan©
Teka-teki ini menang/dimainkan: 16649/25331
Mengapa saya perlu membaca "Makanan untuk Difikirkan" ini?
Kerana anda akan terkejut.
Selepas mencuba beberapa teka-teki pembungkusan, bidang matematik yang anda fikir paling berguna untuk menyelesaikannya:
1) Algebra, 2) Teori Kebarangkalian, 3) Geometri, 4) Teori Nombor, 5) Simetri, 6) Kawasan lain?
Apa yang ternyata paling berguna ialah memikirkan pembahagian nombor, terutamanya boleh dibahagikan dengan 2. Ini adalah subjek Teori Nombor. Perkara yang kita susun adalah objek geometri, tetapi itu tidak bermakna pengetahuan geometri diperlukan untuk menyelesaikan teka-teki. Daripada Geometri kita perlu tahu apakah luas segi empat sama atau segi empat tepat, tetapi tidak lebih.
Untuk sesetengah teka-teki, memikirkan simetri juga sangat berguna.
Petua pantas
Ini adalah petunjuk untuk mereka yang mencari bantuan tetapi tidak berminat dengan latar belakang matematik.
- Dengan melihat nombor di sebelah "Teka-teki ini menang/dimainkan" untuk setiap teka-teki, semak mana yang paling mudah. Bermula dengan teka-teki yang paling mudah sentiasa merupakan idea yang baik, dan akan memberi anda latihan dengan mengendalikan antara muka.
- Teka-teki "2×3×3 1" dan "2×3×3 2" mudah diselesaikan dengan percubaan dan kesilapan.
- Jika percubaan pertama anda pada teka-teki "1×7×10 1" tidak berjaya, putar kepingan pada percubaan anda yang seterusnya.
- "1×7×7 1" ialah teka-teki di mana memikirkan simetri membantu. Sebabnya ialah bekas (grid) mempunyai tapak persegi dengan 4 sisi yang sama panjang, dan kami mempunyai 4 kepingan panjang dengan bentuk yang sama. Oleh itu, seseorang harus meletakkannya secara simetri. Terdapat hanya satu kepingan berbentuk segi empat sama ungu. Untuk mempunyai penyelesaian simetri putaran 90°, bahagian ini mesti berada di tengah. Mana-mana tempat lain akan memecahkan simetri 90° penyelesaian.
- Teka-teki dengan butang yang lebih gelap memerlukan lebih banyak pemikiran. Mulakan dengan memahami sepenuhnya teka-teki "3×3×3 2" sebelum maju ke teka-teki 5×5×5.
Bagaimanakah seseorang boleh menyelesaikan teka-teki ini tanpa percubaan dan kesilapan?
Berikut ialah beberapa petunjuk:
- Bahagikan masalah yang sukar kepada yang lebih mudah, iaitu kepada sub-matlamat. Sebagai contoh, untuk mengisi keseluruhan bekas, seseorang perlu mengisi setiap lapisan.
- Susun kepingan dengan cara simetri, terutamanya jika bekas simetri seperti kiub 3×3×3 atau bekas berbentuk persegi 1×7×7.
- Manfaatkan sepenuhnya maklumat yang diberikan. Apakah saiz kepingan? Berapa ramai daripada mereka mempunyai bentuk yang sama?
Baki "Makanan untuk Difikirkan" ini mempunyai matlamat untuk menyelesaikan semua teka-teki tanpa percubaan dan kesilapan, sebaliknya mengemukakan soalan mudah dan menjawabnya.
Definisi
Untuk kejelasan, berikut ialah beberapa istilah yang akan kami gunakan untuk membincangkan masalah pembungkusan:
Sekeping
Salah satu bentuk yang akan disatukan untuk membentuk pepejal yang lebih besar.
Sekeping ganjil ialah kepingan yang panjangnya semuanya ganjil, seperti kepingan 1×1×1 atau kepingan 1×3×5.
Sekeping adalah walaupun ia mempunyai sekurang-kurangnya dua panjang genap, seperti 1×2×4 atau 2×2×2.
Adakah semua kepingan sama ada genap atau ganjil?
TIDAK. Sekeping dengan tepat satu panjang genap, seperti 1×2×3, tidak sesuai dengan mana-mana definisi. Dalam bahagian berikut, kami akan memberi tumpuan kepada kepingan ganjil dan genap.
Kubus/Bekas
Kubus ialah prisma segi empat tepat. Kami menggunakan perkataan "bekas" untuk merujuk kepada cangkerang kosong kuboid. Kami merujuk kepada "kuboid" sebagai kandungan bekas. Bekas hendaklah diisi dengan kepingan dan kuboid dicipta daripada kepingan.
Lapisan
Lapisan ialah kepingan ketebalan 1 ke arah selari dengan muka bekas. Bekas 3×4×5 mempunyai 3 lapisan saiz 4×5, 4 lapisan saiz 3×5, dan 5 lapisan saiz 3×4.
Berapakah bilangan lapisan bekas 1×5×7?
Ia mempunyai satu lapisan 5×7, lima lapisan 1×7, dan tujuh lapisan 1×5. Secara keseluruhan ia mempunyai 1 + 5 + 7 = 13 lapisan.
Cube
Khususnya, kiub 1×1×1, bukan kiub yang lebih besar. Sekeping 1×1×1 terdiri daripada 1 kiub, manakala kepingan 1×1×3 terdiri daripada 1 × 1 × 3 = 3 kiub.
Blok Bangunan
Beberapa kepingan yang melekat antara satu sama lain membentuk Blok Bangunan. Blok binaan yang menarik akan mempunyai simetri. Untuk teka-teki yang lebih sukar, beberapa blok binaan yang serupa atau serupa cermin serta bahagian tengah akan mengisi bekas.
Strategi
Separuh daripada penyelesaian masalah yang sukar adalah untuk membahagikan masalah sukar kepada masalah yang lebih kecil.
Untuk melakukan ini, seseorang harus bertanya kepada diri sendiri soalan mudah. Soalan-soalan berikut akan berguna dalam menyelesaikan teka-teki pembungkusan.
Bolehkah setiap kuboid dibentuk dengan kepingan saiz 1×2×2 ? Sebagai contoh, bolehkah kuboid 3×3×3 dibentuk hanya menggunakan kepingan saiz 1×2×2 ?
TIDAK. Sekeping 1×2×2 terdiri daripada bilangan kiub genap. Oleh itu, sebarang bilangan kepingan 1×2×2 bersama-sama akan mempunyai jumlah kiub yang genap. Oleh kerana kuboid 3×3×3 terdiri daripada bilangan kiub ganjil, ia tidak boleh dibentuk dengan cara ini.
Dalam beberapa bahagian seterusnya, kita akan meneroka bagaimana kebolehbahagian, terutamanya oleh 2, menentukan cara kepingan mesti diletakkan untuk menyelesaikan teka-teki tertentu.
Bolehkah kepingan 1×2×2 sekurang-kurangnya mengisi mana-mana lapisan bekas 3×3×3?
Jawapannya sekali lagi TIDAK. Kawasan dalam lapisan yang boleh diduduki oleh sekeping ialah luas salah satu muka kepingan itu, bukan?
Apakah wajah sekeping 1×2×2?
Sekeping 1×2×2 mempunyai dua pasang muka 1×2 selari, dan sepasang muka 2×2.
Apakah kawasan muka ini, dan apakah persamaan kawasan tersebut?
Kawasannya ialah 1 & kali 2 = 2 dan 2 & kali 2 = 4. 2 dan 4 kedua-duanya ialah nombor genap.
Kami memerhatikan bahawa sekeping 1×2×2 hanya boleh menduduki bilangan kiub genap (2 atau 4) dalam setiap lapisan.
Adakah ini benar untuk semua kepingan genap?
Setiap muka sekeping mempunyai dua panjang. Oleh kerana kepingan genap mempunyai paling banyak satu panjang ganjil, maka setiap muka mereka akan mempunyai sekurang-kurangnya satu panjang genap. Kerana genap & kali ganjil = genap, luas setiap muka akan menjadi genap. Inilah sebabnya kami memanggilnya kepingan genap!
Kami mengetahui bahawa kuboid dengan panjang sisi ganjil tidak boleh dibentuk daripada kepingan genap sahaja. Lapisan dengan kawasan ganjil juga tidak boleh diisi dengan kepingan genap. Oleh itu, teka-teki "3×3×3 2" mempunyai beberapa kepingan 1×1×1, yang merupakan kepingan ganjil.
Berikut ialah satu lagi soalan berguna untuk dipertimbangkan:
Adakah salah satu daripada dua jenis kepingan (1×1×1 dan 1×2×2) lebih 'berharga' daripada yang lain?
YA. Jika kita hanya mempunyai kepingan 1×1×1, maka sebarang teka-teki akan menjadi remeh, adakah anda setuju? Jika kita hanya mempunyai 1×2×2 keping, maka bekas ganjil tidak boleh diisi, seperti yang ditunjukkan di atas.
Soalan yang jelas ialah: Berapakah bilangan minimum keping 1×1×1 yang boleh mengisi bekas 3×3×3?
Sememangnya, soalan-soalan berikut timbul:
Mengapa tiga keping 1×1×1 cukup?
Untuk menjawab soalan ini, kita akan membandingkan bilangan lapisan ganjil (lapisan dengan kawasan ganjil) dengan bilangan lapisan kawasan ganjil yang boleh diisi dengan kepingan genap dan hanya 3 kiub.
Berapakah bilangan lapisan bekas 3×3×3?
Dalam setiap tiga arah (lebar, tinggi, kedalaman), bekas mempunyai 3 lapisan. Terdapat 3 + 3 + 3 = 9 lapisan ganjil yang diisi apabila bekas diisi.
Berapakah bilangan lapisan ganjil 3×3 yang boleh dilengkapkan dengan satu keping 1×1×1 (dan sesetengahnya 1×2×2 keping)?
Tiga lapisan: lapisan mendatar dan dua lapisan menegak yang mengandungi kepingan 1×1×1. Oleh itu, 3 kiub boleh membantu mengisi paling banyak 3 & kali 3 = 9 lapisan.
Ini menunjukkan bahawa 3 kiub diperlukan, dan kerana teka-teki "3×3×2 2" boleh diselesaikan, 3 kiub juga mencukupi untuk mengisi 9 lapisan ganjil.
Apa yang memberitahu kita tentang lokasi 3 kiub dalam
Teka-teki "3×3×3 2"?
Dalam setiap 9 lapisan hanya boleh ada 1 kiub, bukan 0 kiub dan bukan 2 kiub! Jika tidak, 3 kiub tidak akan mencukupi untuk 9 lapisan.
Ini adalah kejayaan untuk penyelesaian. Tambahan pula, satu-satunya cara untuk meletakkan kiub adalah di sepanjang pepenjuru - dengan satu kiub di tengah, dan dua kiub lain di sudut bertentangan secara menyerong. Jika tidak, kepingan 1×2×2 yang besar akan terlalu besar untuk mengisi ruang di sekeliling 3 kiub.
Oleh itu, letakkan satu kiub di sudut, dan tiga keping 1×2×2 secara simetri di sekeliling kiub itu. Letakkan satu kiub di tengah, satu di sudut bertentangan, dan selebihnya akan jelas.
Apa lagi yang boleh kita pelajari daripada penyelesaian ini? Sebagai contoh, adakah ia mempunyai simetri?
Simetri boleh dilihat selepas meletakkan kiub pertama di sudut dan tiga kepingan 1×2×2 di sekelilingnya. Penyelesaiannya mempunyai simetri putaran 120° dengan pepenjuru kiub sebagai paksi putaran (120° = 1/3 daripada putaran bulatan penuh).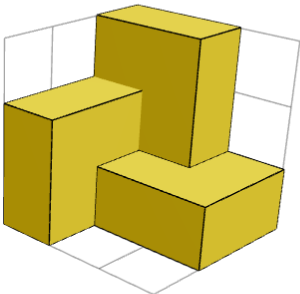
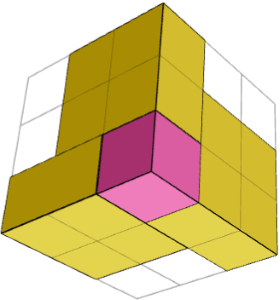
Adakah penyelesaiannya jumlah blok binaan yang sama atau simetri, masing-masing terdiri daripada beberapa keping?
YA. Kubus ialah jumlah 2 blok binaan yang simetri cermin (1 kiub di sudut + tiga keping 1×2×2 di sekelilingnya) dan satu kiub di tengah. 2 imej di atas menunjukkan satu blok bangunan dari 2 sisi.
Adakah terdapat cara lain untuk menyelesaikan teka-teki ini menggunakan blok binaan yang berbeza?
YA. Imej kiri dan kanan di bawah menunjukkan dua blok binaan simetri cermin untuk teka-teki "3×3×3 2". Mereka boleh digabungkan dengan kiub tengah (imej tengah) untuk menyelesaikan teka-teki.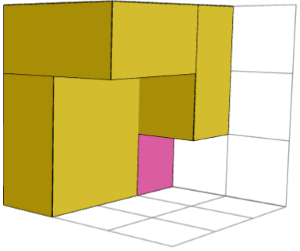
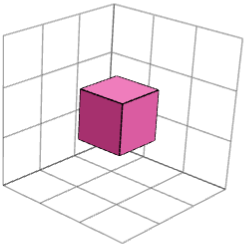
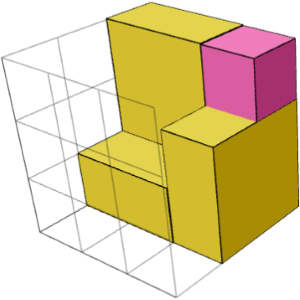
Mengapa kita perlu bersusah payah memikirkan blok binaan?
Lebih mudah untuk menggunakan sebilangan kecil kepingan yang diberikan dan mencipta sesuatu yang simetri daripadanya, daripada mengisi bekas yang lebih besar dengan semua kepingan.
Bolehkah blok binaan digunakan untuk menyelesaikan teka-teki yang lebih besar, seperti "3×5×7 1"?
YA. Bekas yang lebih besar, walaupun panjangnya berbeza, boleh diisi menggunakan blok binaan simetri yang sama/cermin. Terdapat pelbagai cara untuk menyelesaikan teka-teki "3×5×7 1" menggunakan blok binaan dan kepingan ganjil tengah. Kami serahkan kepada anda untuk mencari beberapa contoh.
Bagaimanakah kita tahu bahagian mana yang harus membentuk blok binaan?
Mari kita fikirkan tentang pusat kuboid ganjil terlebih dahulu. Oleh kerana kedudukan tengah adalah unik, jika kita mahukan penyelesaian simetri, pusat mesti diduduki oleh sekeping dengan bentuk yang sama dengan bekas. Kubus 3×3×3 ialah kiub jadi bahagian tengah untuk itu mestilah kiub. Sekeping 1×2×2 di tengah akan memecahkan simetri.
Ini bermakna kita mempunyai 6 kuning dan 3 − 1 = 2 kepingan merah jambu untuk membina beberapa blok binaan yang sama.
Berapa banyak blok binaan yang perlu kita cuba buat?
Blok binaan harus membentuk kuboid tolak bahagian tengah. Oleh itu, bilangan kepingan kuning dalam blok bangunan mestilah pembahagi 6 (jumlah blok kuning) dan bilangan kepingan merah jambu blok bangunan perlu membahagikan 2 (bilangan kiub merah jambu yang tinggal selepas menempah satu untuk pusat).
Oleh itu, nombor N blok binaan yang sama ialah pembahagi persekutuan terbesar bagi bilangan kepingan yang sama, di sini 6 dan 2, iaitu GCD(6,2) = 2. Oleh itu, kita harus membuat blok bangunan dari 2 / 2 = 1 kiub merah jambu dan 6 / 2 = 3 blok kuning. Inilah yang kami lakukan.
Ringkaskan algoritma matematik untuk menggunakannya untuk teka-teki yang lebih besar.
Untuk bekas ganjil:
- Sejajarkan kepingan ganjil untuk memastikan ia tidak bertindih dalam mana-mana lapisan. Mereka harus menghubungkan satu sudut bekas dengan sudut bertentangan bekas. Jika kepingan ganjil adalah kiub, mereka membentuk pepenjuru. Jika kepingan ganjil lebih besar (1x1x3), maka ia membentuk pepenjuru tidak lurus.
- Jika terdapat hanya satu jenis sekeping genap, maka gunakannya untuk mengisi bekas.
- Sekiranya terdapat pelbagai jenis kepingan genap:
- Ketepikan bahagian ganjil tengah. Dari kepingan yang selebihnya, cari pembahagi persekutuan terbesar N daripada bilangan kepingan jenis yang berbeza. N ialah bilangan blok bangunan.
- Buat N blok binaan yang sama dan letakkan bersama-sama dengan bahagian tengah sekiranya terdapat bekas ganjil.
Walaupun teka-teki kecil boleh diselesaikan dengan mudah melalui percubaan dan kesilapan, strategi ini tidak berfungsi untuk teka-teki yang lebih besar. Penerokaan kami terhadap kepingan ganjil dan genap mendedahkan sebab penting: penempatan kepingan ganjil adalah penting, kerana terdapat sangat sedikit cara ia boleh diletakkan dengan betul. Menggunakan percubaan dan kesilapan, seseorang boleh membuat kesilapan pada permulaan dan hanya menyedari bahawa ada sesuatu yang tidak kena selepas meletakkan banyak keping. Ini menjadikannya sangat sukar untuk menentukan apa yang menyebabkan ralat, jadi tiada maklum balas yang boleh digunakan; Kaedah percubaan dan kesilapan tidak berkesan untuk bekas yang lebih besar. Berfikir diperlukan.
Pembungkusan dengan hanya satu jenis kepingan
Dalam bahagian ini kita akan meneroka saiz kuboid yang boleh dibentuk daripada satu jenis keping. Ini adalah bahagian teori, tidak diperlukan untuk menyelesaikan teka-teki di atas. Bahagian ini tidak memerlukan matematik yang sukar.
Dengan kepingan 1×1×1 yang mencukupi, kita boleh dengan mudah membentuk kuboid dalam sebarang saiz. Tetapi bagaimana pula dengan kepingan lain, seperti kepingan 2×3×4 atau 1×2×5? Terdapat dua soalan utama untuk disiasat. Pertama, memandangkan panjang sekeping dan panjang kuboid, bagaimanakah kita boleh menentukan sama ada kuboid boleh dicipta daripada salinan sekeping itu? Kedua, bagaimanakah kita, bermula daripada satu bahagian, menjana panjang kuboid yang boleh dibentuk? Sepanjang bahagian ini, kami akan mempertimbangkan soalan yang lebih mudah sambil meneroka dua masalah penting ini.
Bolehkah kuboid 2×6×10 dibentuk daripada hanya 1×2×5 keping?
YA! Tiga kepingan 1×2×5 boleh diletakkan bersebelahan untuk membentuk bentuk 1×6×5 (3 × 2 = 6). Kita kemudian boleh mencipta bentuk 1×6×5 kedua dan menggabungkannya menjadi bentuk 1×6×10. Akhir sekali, dua bentuk 1×6×10 boleh diletakkan bersama untuk membentuk kuboid 2×6×10.
Adakah mungkin untuk membentuk kuboid 10×12×14 hanya menggunakan kepingan saiz 2×5×6?
Pembayang
Tidak perlu membayangkan bagaimana kepingan itu akan disusun.
Petunjuk lain?
Sekeping 2×5×6 adalah sama dengan kepingan 5×6×2 kerana ia boleh diputar.
Jawapan
YA. Oleh kerana 10 / 5 = 2, 12 / 6 = 2, dan 14 / 2 = 7, kuboid yang lebih besar boleh dianggap sebagai susunan 2×2×7 bagi kepingan 5×6×2. Kepingan 5×6×2 semuanya boleh diletakkan dengan orientasi yang sama.
Bagaimanakah kita boleh menyamaratakan penemuan ini?
Katakan kita hanya mempunyai kepingan saiz x × y × z. Kemudian membina kuboid X & kali Y & kali Z adalah mungkin jika terdapat integer positif A, B, C supaya Ax, By dan Cz sama dengan X, Y dan Z dalam beberapa susunan.
Berapa banyak kepingan yang akan digunakan dalam kes ini?
Kita boleh menyusun kepingan A dalam satu arah, B dalam arah lain, dan C dalam arah ketiga. Secara keseluruhan kepingan A & kali B & kali C akan digunakan.
Mengapa Ax, By dan Cz boleh sama dengan X, Y dan Z dalam sebarang susunan?
Bekas bersaiz X & kali Y & kali Z adalah sama dengan kubus Z & kali X & kali Y . Susunan panjang tidak penting kerana kuboid boleh diputar.
Adakah benar bahawa mana-mana kuboid yang terbentuk daripada kepingan 1×2×3 mesti mempunyai panjang A, B × 2, C × 3, untuk beberapa integer positif A, B, C ?
TIDAK. Jika semua kepingan 1×2×3 berorientasikan ke arah yang sama, kuboid akan mempunyai saiz A × (B × 2) × (C × 3). Tetapi kepingan boleh berorientasikan secara berbeza dan masih membentuk kuboid. Sebagai contoh, kepingan 1×2×3 boleh membentuk kuboid 1×5×6, walaupun 1, 5 dan 6 tidak sama dengan A, B × 2, dan C × 3 dalam sebarang susunan. Contoh lain ialah teka-teki "1×7×10 1", yang terdiri daripada kepingan 1×2×5.
Apakah hubungan antara panjang kepingan dan panjang kuboid dalam kedua-dua contoh ini?
Dalam kedua-dua contoh ini, salah satu panjang kuboid ialah jumlah dua panjang bahagian itu. Panjang kuboid yang berbeza ialah LCM (Gandaan Komet Terendah) bagi dua panjang kepingan yang sama. Dalam kes kuboid 1×5×6 yang terbentuk daripada kepingan 1×2×3, kita mempunyai 1×5×6 = 1 × (2 + 3) × LCM(2,3). Begitu juga, 1×7×10 = 1 × (2 + 5) × LCM(2,5).
Bagaimanakah kita boleh menggunakan fakta ini untuk mencari cara menjana panjang kuboid yang boleh dibina daripada kepingan tertentu?
Kami mulakan dengan mewakili panjang sekeping sebagai tiga kali ganda yang dipesan. Sebagai contoh, sekeping 1×2×3 diwakili oleh (1, 2, 3). Sekarang, terdapat 3 operasi yang boleh kita lakukan berulang kali untuk memberikan panjang kuboid yang boleh dibentuk daripada bahagian ini. Mereka ialah:
- Tukar susunan panjang. Ini dikenali sebagai permutasi. Dalam kes kami, ia mewakili putaran dalam ruang 3 dimensi. Contohnya ialah
(1, 2, 3) → (2, 3, 1). - Darabkan panjang dengan integer positif A, B dan C, masing-masing. Ini sepadan dengan membentuk kuboid yang lebih besar dengan meletakkan kepingan A dalam satu arah, B ke arah lain, dan C di sepanjang arah ketiga. Sebagai contoh, kita boleh darab dengan 1, 4, dan 3 untuk memberikan (1, 2, 3) → (1 & kali 1, 4 & kali 2, 3 & kali 3) = (1, 8, 9).
- Ambil dua panjang dan gantikan satu dengan jumlah mereka dan satu dengan LCM mereka.. Ini sepadan dengan membentuk kuboid yang lebih besar dengan kepingan yang berorientasikan ke arah yang berbeza. Sebagai contoh, memilih panjang 2 dan 3, kita akan memperoleh (1, 2, 3) → (1, 2 + 3, LCM(2,3)) = (1, 5, 6).
Bolehkah seseorang menggabungkan kepingan dalam carake-4 untuk menghasilkan kuboid yang bentuknya berbeza daripada hasil operasike-3 ?
YA. Pertimbangkan sekeping saiz x × y × z. Operasi ketiga menghasilkan kuboid saiz x × (y + z) × LCM(y,z), di mana satu panjang x tidak berubah dari kepingan ke kuboid.
Cara yang serupa tetapi berbeza ialah meletakkan semula LCM(y,z)/y banyak kepingan bersebelahan antara satu sama lain dan LCM(y,z)/y banyak kepingan bersebelahan antara satu sama lain, seperti sebelum ini, tetapi sekarang untuk memutar satu set sebanyak 90° supaya kedua-dua blok mempunyai panjang LCM(y,z) yang sama, tetapi ketinggian yang berbeza. Dari segi matematik, kami tidak melampirkan x & kali y & kali LCM(y,z) dan x & kali z & kali LCM(y,z) untuk membentuk x & kali (y + z) & kali LCM(y,z). Sebaliknya, salah satu daripadanya, katakan, x & kali z & kali LCM(y,z), diputar kepada z & kali x & kali LCM(y,z) dan kemudian dilampirkan.
Kawasan asas segi empat tepat kemudiannya bukan (y + z) &kali LCM(y,z), tetapi (x + z) &kali LCM(y,z). Kemudian dua blok binaan x × y × LCM(y,z) dan z × x × LCM(y,z) masing-masing mempunyai panjang x dan z, dalam arah X.
Menyusun LCM(x,z)/x banyak blok binaan ketinggian x dan LCM(x,z)/z banyak blok binaan ketinggian z, kedua-dua timbunan mencapai ketinggian LCM(x,z). Apabila ia dilampirkan, hasilnya ialah kuboid saiz LCM(x,z) × (x + z) × LCM(y,z), yang mempunyai bentuk dan saiz yang berbeza daripada mana-mana kuboid yang terhasil daripada operasi ketiga.
Seseorang boleh mengulangi operasi ini dalam sebarang susunan, mula-mula menjana kuboid daripada sekeping, dan kemudian menggunakan kuboid sebagai "sekeping" untuk menjana kuboid yang lebih besar. Kami telah membincangkan sebelum ini bagaimana kuboid 2×6×10 boleh dibentuk daripada kepingan 1×2×5. Dalam kes ini hanya satu operasi diperlukan, darabkan dengan 2, 3 dan 2, masing-masing: (1, 2, 5) → (2 & kali 1, 3 & kali 2, 2 × 5) = (2, 5, 10).
Oleh itu, kepingan saiz x × y × z bukan sahaja boleh membina kuboid saiz Ax × By × Cz tetapi, sebagai contoh, juga dengan saiz x × (y + z) × LCM(y,z), di mana LCM(y,z) ialah Gandaan Sesama Terendah bagi y dan z. Meletakkan beberapa blok binaan ini bersama-sama memberikan kuboid bersaiz Axe × B(y + z) + C(LCM(y,z)).
Kami kini akan mempertimbangkan jenis kepingan khas. Sekeping adalah harmonik jika setiap panjangnya yang lebih besar boleh dibahagikan dengan panjang yang lebih kecil seterusnya. Sebagai contoh, sekeping 1×2×6 adalah harmonik kerana 2 / 1 = 1 dan 6 / 2 = 3. Sekeping 1×4×6 tidak harmonik kerana 6 bukan gandaan 4.
Adakah sekeping 1×2×3 harmonik?
TIDAK, kerana 3 tidak boleh dibahagikan dengan 2.
Apa yang menjadikan kepingan harmonik istimewa dalam pembungkusan? Bagaimanakah ia berkaitan dengan perbincangan kita tentang panjang kepingan dan kuboid?
Kami telah memerhatikan bahawa mana-mana kepingan boleh membentuk kuboid yang panjangnya adalah gandaan daripada panjang kepingan itu. Ternyata panjang mana-mana kuboid yang dibentuk oleh kepingan harmonik yang sama mestilah gandaan panjang kepingan. Iaitu, jika kepingan harmonik mempunyai panjang x, y dan z, mana-mana kuboid yang terbentuk daripada salinan kepingan ini mesti mempunyai satu panjang boleh dibahagikan dengan x, satu lagi boleh dibahagikan dengan y, dan yang ketiga boleh dibahagikan dengan z. Walaupun ini adalah kenyataan yang mudah, bukti memerlukan konsep di luar skop laman web ini. Pautan ke bukti boleh didapati di bahagian "Pengakuan".
Bagaimanakah fakta ini konsisten dengan empat operasi yang kita bincangkan di atas?
Kita boleh mulakan dengan memikirkan sekeping sebagai juga kuboid yang terbentuk daripada satu salinan kepingan itu. Sekeping x & kali y & kali z juga merupakan kubus x & kali y & kali z . Panjang kuboid ini adalah gandaan daripada panjang kepingan, kerana setiap nombor adalah gandaan dirinya sendiri. Kami akan menunjukkan mengapa empat kaedah yang kami perkenalkan menghasilkan kuboid yang panjangnya masih gandaan panjang kepingan.
- Menukar susunan panjang (pilih aturatur): ini hanyalah putaran, dan sebenarnya tidak mengubah panjang kuboid. Panjang kuboid masih akan menjadi gandaan panjang kepingan.
- Darabkan panjang kuboid dengan integer positif: jika panjang kuboid sudah gandaan panjang kepingan, ini tidak akan berubah. Mereka hanya akan menjadi gandaan yang lebih besar. Jika X = Kapak ialah gandaan x, maka DX = DAx juga merupakan gandaan x, untuk mana-mana integer positif D.
- Menggantikan dua panjang dengan jumlah dan LCM: inilah sebabnya mengapa kepingan harmonik adalah penting; kita perlu menggunakan definisi kepingan harmonik. Katakan kita bermula dengan sekeping harmonik (x, y, z), dari mana kita telah membentuk kuboid (Ax, By, Cz). Susunan panjang tidak penting kerana kuboid boleh diputar. Kami kini akan melakukan operasi ketiga pada mana-mana dua panjang kuboid, katakan Kapak dan Oleh: (Kapak, Oleh, Cz) → (Kapak + Oleh, LCM(Kapak, Oleh), Cz). Sekarang, kerana kepingan (x, y, z) adalah harmonik, salah satu daripada dua panjang x dan y adalah gandaan yang lain. Katakan y ialah gandaan x. Oleh itu, By juga merupakan gandaan x, dan kerana Ax juga, jumlah Ax + By ialah gandaan x. Seterusnya, LCM(Kapak,Oleh) ialah gandaan persekutuan terendah bagi Kapak dan Oleh, jadi ia mengikut definisi gandaan Oleh, oleh itu ia boleh dibahagikan dengan y. Akhir sekali, Cz, sudah tentu, gandaan z. Oleh itu, panjang kuboid baharu (Kapak + Oleh, LCM(Kapak,Oleh), Cz) masih gandaan panjang kepingan.
- Bagaimana pula dengan operasi keempat? Oleh kerana operasi ini serupa dengan operasi ketiga, hujah yang dikemukakan di atas boleh disesuaikan untuk kes ini. Kami membiarkannya sebagai latihan.
Kami telah menunjukkan bahawa empat operasi, yang dilakukan berulang kali dalam sebarang susunan pada mana-mana bahagian harmonik, akan menghasilkan kuboid yang panjangnya adalah gandaan panjang kepingan. Adalah penting untuk ambil perhatian bahawa dalam perbincangan kami tentang operasi ketiga (dan keempat!), kami bergantung pada fakta bahawa karya itu harmonik. Apabila sekeping tidak harmonik, hujah itu gagal. Inilah perbezaan utama antara kepingan harmonik dan bukan harmonik. Untuk kepingan harmonik, kaedah ketiga dan keempat tidak menghasilkan bentuk tambahan berbanding dua kaedah pertama.
Akibatnya, mana-mana kuboid yang terbentuk daripada kepingan harmonik boleh mempunyai semua kepingan dalam orientasi yang sama. Oleh itu, jika kita cuba membentuk kuboid daripada kepingan harmonik yang sama, sudah cukup untuk cuba menyusun semuanya menghadap ke arah yang sama. Jika ini tidak mungkin, maka kuboid tidak boleh dibentuk sama sekali.
Oleh kerana kepingan 1×2×2 adalah harmonik, mana-mana kuboid yang terbentuk daripada salinan kepingan ini mesti mempunyai panjang A, B × 2, dan C × 2 untuk beberapa integer A, B, dan C. Imej di bawah menunjukkan kuboid 5×4×4 yang dibentuk oleh kepingan 1×2×2, yang semuanya mempunyai orientasi yang sama.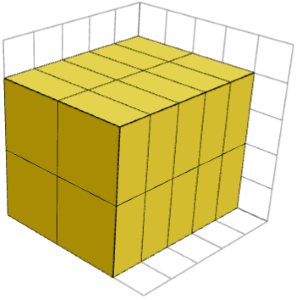
Apakah nilai A, B dan C ?
Menetapkan A, B × 2, dan C × 2 sama dengan 5, 4, dan 4, masing-masing, kita dapati A = 5 / 1 = 1, B = 4 / 2 = 2, dan C = 4 / 2 = 2.
Apabila membungkus dengan kepingan harmonik, adakah kepingan itu perlu menghadap ke arah yang sama?
TIDAK! Walaupun semua kepingan sentiasa mungkin mempunyai orientasi yang sama, mungkin terdapat susunan lain, tetapi ia tidak membentuk bentuk baharu. Imej di bawah menunjukkan cara yang berbeza untuk membentuk kuboid 5×4×4 daripada kepingan 1×2×2.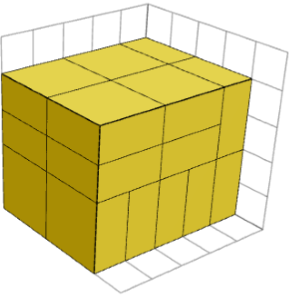
Apakah peraturan untuk kepingan bukan harmonik?
Apabila bekerja dengan sekeping bukan harmonik x × y × z, terdapat beberapa kuboid yang boleh dibentuk yang saiznya bukan Ax × By × Cz untuk mana-mana integer A, B, C. Sebagai contoh, kuboid 1×5×6 boleh dicipta daripada kepingan 1×2×3. Ini adalah hasil daripada operasi ketiga, seperti yang dibincangkan sebelum ini.
Adalah penting untuk ambil perhatian bahawa bilangan kiub dalam kuboid mesti sentiasa boleh dibahagikan dengan bilangan kiub dalam bahagian itu. Apabila panjang kiub bukan setiap gandaan panjang kepingan yang berbeza, salah satu panjang kuboid akan menjadi gandaan biasa sekurang-kurangnya 2 panjang kepingan, disebabkan oleh kaedah ketiga dan keempat. Fakta ini boleh digunakan untuk menentukan sama ada kuboid tertentu boleh dibentuk daripada kepingan bukan harmonik.
Beberapa soalan untuk mengkaji semula apa yang telah kami terokai:
Bolehkah 2×4×12 kepingan membentuk kuboid bersaiz 4×8×36? Bagaimana pula dengan kuboid bersaiz 10×10×12 ?
Oleh kerana 4 / 2 = 2, 8 / 4 = 2, dan 36 / 12 = 3, kuboid 4×8×36 boleh terbentuk.
Salah satu panjang kuboid 10×10×12 boleh dibahagikan dengan 12. Panjang lain ialah 10 dan 10, kedua-duanya tidak boleh dibahagikan dengan 4. Oleh itu, panjang kuboid 10×10×12 bukanlah gandaan panjang kepingan. Oleh kerana 12 / 4 = 3 dan 4 / 2 = 2, kepingan itu adalah harmonik, oleh itu kuboid 10×10×12 tidak boleh dibentuk daripada kepingan bersaiz 2×4×12.
Bolehkah kepingan saiz 1×3×5 membentuk kuboid saiz 2×15×8 ? Bagaimana pula dengan kuboid 3×9×14?
Oleh kerana 5 tidak boleh dibahagikan dengan 3, bahagian itu tidak harmonik. Kita tidak boleh menggunakan pengetahuan kita tentang kepingan harmonik.
Adalah mungkin untuk membentuk kuboid 2×15×8 dengan kepingan ini. Tiga keping 1×3×5 boleh membentuk bentuk 1×3×15 (atau 1×15×3), dan 5 daripada kepingan yang disusun secara berbeza boleh membentuk bentuk 1×15×5. Kedua-dua bentuk ini boleh digunakan untuk mencipta kuboid 1×15×8, dua daripadanya boleh membentuk kuboid 2×15×8. Kita boleh menggunakan operasi yang kita bincangkan untuk menjadi lebih ringkas: (1, 3, 5) → (1, 3 + 5, LCM(3,5)) = (1, 8, 15) → (2, 8, 15) → (2, 15, 8).
Setiap kali 1×3×5 kepingan digabungkan, jumlah bilangan kiub ialah gandaan 5. Oleh kerana 3 × 9 × 14 tidak boleh dibahagikan dengan 5, kuboid 3×9×14 tidak boleh dicipta daripada kepingan saiz 1×3×5.
Ringkasan peraturan untuk kepingan harmonik dan bukan harmonik
Berikut ialah gambaran keseluruhan perkara yang telah kami pelajari:
- Jika panjang kuboid adalah gandaan panjang sekeping, maka ia boleh dibentuk daripada salinan kepingan itu, tidak kira sama ada kepingan itu harmonik. Kubus sedemikian boleh dibentuk dengan semua kepingan dalam orientasi yang sama, tetapi mungkin juga terdapat susunan di mana kepingan mempunyai orientasi yang berbeza.
- Jika sekeping adalah harmonik, maka mana-mana kuboid yang terbentuk mesti mempunyai panjang yang merupakan gandaan daripada panjang kepingan itu. Akibatnya, mana-mana kuboid yang terbentuk daripada kepingan harmonik mungkin mempunyai semua kepingan dalam orientasi yang sama, walaupun ini tidak selalu diperlukan.
- Jika sekeping tidak harmonik, terdapat beberapa kuboid yang boleh dibentuk yang panjangnya bukan gandaan panjang kepingan (lihat operasi ketiga dan keempat). Dalam kes ini, kepingan tidak boleh mempunyai orientasi yang sama. Menggunakan kepingan bukan harmonik, seseorang boleh mencipta kuboid dengan bentuk yang berbeza dengan menggunakan 4 kaedah yang diterangkan sebelum ini.
Adakah pemerhatian ini hanya sah dalam tiga dimensi?
TIDAK. Dalam konteks ini, tidak ada yang istimewa tentang 3 dimensi. Malah, menetapkan salah satu panjang sama dengan 1 adalah bersamaan dengan mengurangkan masalah kepada 2 dimensi. Hasilnya juga sah dalam lebih daripada 3 dimensi. Sebagai contoh, sekeping 1×3×12×24 adalah harmonik. Oleh itu, mana-mana kuboid 4 dimensi yang terbentuk daripada kepingan 4 dimensi ini mesti mempunyai dimensi A, B × 3, C × 12 dan D × 24 untuk beberapa integer positif A, B, C, dan D.
Bagaimana untuk mendapatkan teka-teki hands-on?
Kami tidak boleh memberitahu anda cara membuat kepingan 4 dimensi :) Tetapi dalam 3 dimensi jika anda mempunyai banyak dadu ganti, anda boleh menempelkannya bersama-sama untuk membentuk kepingan.
Daripada kotak 5×5×5, seseorang boleh menggunakan, sebagai contoh, kotak kasut. Jika seseorang memegangnya secara menyerong, kepingan itu akan kekal di tempat ia diletakkan.
Sesetengah teka-teki mempunyai ketinggian 1 (contohnya, "1×7×10 1") dan oleh itu merupakan teka-teki 2 dimensi. Seseorang boleh memotong segi empat tepat daripada kertas graf untuk digunakan sebagai kepingan untuk teka-teki ini.
Pengesahan
Minat kami untuk membungkus teka-teki tercetus apabila melihat versi kayu teka-teki "5x5x5 1" di pameran matematik. Berikutan rujukan kepada pengarangnya, ahli matematik terkenal John Horton Conway, kami menemui teka-teki "3x3x3 2", "5x5x5 2", dan "5x5x5 3" daripadanya.
Bahagian "Pembungkusan dengan hanya satu jenis sekeping" diilhamkan oleh karya ahli matematik Belanda de Bruijn. Untuk mengetahui lebih lanjut tentang pemerhatian de Bruijn mengenai pembungkusan kepingan segi empat tepat, rujuk artikel ini. Anda boleh membaca bukti de Bruijn tentang sifat kepingan harmonik di sini.
Ikuti atau langgan untuk kemas kini: