Floodfill©
Nombre de victoires: 209822
Un Guide pour Jouer à Floodfill
Utiliser un nombre minimal de couleurs pour colorier une carte est un problème dont l’histoire est longue, tel qu’en témoigne l'article de Wikipédia sur Le Théorème des Quatre Couleurs. Le théorème que 4 couleurs suffisent toujours pour colorier une carte plane est devenu célèbre en tant que le premier grand théorème mathématique qui exigeait une démonstration mathématique par ordinateur plutôt que par un humain.
Il n’existe aucun algorithme connu de nos jours qui colorie les cartes de manière efficace. Par « efficace » on entend que si le nombre de régions N est très grand, alors le nombre d’essais de coloriage augmente selon Nk où k est un nombre qui ne dépend pas de N. Autrement dit, pour un algorithme « efficace », le nombre d’essais augmente selon un polynôme de N. Or, les algorithmes de coloration ont une complexité exponentielle. C'est-à-dire, le nombre d’essais dépend de N comme 4N.
Si on permet l’utilisation de cinq ou six couleurs, ou si la carte ne nécessite que 2 couleurs, alors des algorithmes efficaces sont connus.
Une autre occasion d'obtenir une méthode efficace est de ne plus exiger que l'algorithme soit TOUJOURS efficace. On décrit ci-dessous une telle heuristique (ou un ensemble d'instructions) qui fonctionne, au moins, dans un bon nombre de cas:
- Il est utile de colorier en premier une région qui a le plus grand nombre de voisins possible car lorsque celle-ci reçoit la couleur A, tous ses voisins reçoivent une restriction de ne pas recevoir la couleur A. Ainsi réduit-on le nombre de choix de couleurs pour ces régions voisines et de même le nombre d’essais plus tard se la coloration s’avère difficile.
- La première couleur utilisée est sans restriction.
- La première fois qu’on utilise une deuxième couleur, le choix de couleur est sans restriction si cette région est adjacente à une région de la première couleur (c.-à-d. quand il faut une deuxième couleur).
- La première fois qu’on utilise une troisième couleur, le choix de couleur est sans restriction si cette région est adjacente à une région de la première couleur et à une région de la deuxième couleur (c.-à-d. quand il faut une troisième couleur).
- La prochaine région à colorier est celle où il ne reste qu’une seule couleur à choisir, de sorte qu’il est impossible de se tromper.
- Le nombre d’essais de coloration est certainement inférieur à 4N (en essayant toutes les 4 couleurs pour toutes les N régions). Alors le nombre d’essais de coloration dépend du nombre de régions N. Par conséquent, il est utile de colorier une région qui divise la partie blanche (incolore) de la carte en de petites mini-cartes séparées qu’on peut ensuite colorier individuellement. Ces régions se composent de N1 et N2 régions (N = N1 + N2) seulement. En plus, il ne faut maintenant qu’au plus 4N1 + 4N2 essais, ce qui est bien inférieur à 4N1 × 4N2 = 4N essais.
- Si on veut trouver le plus petit nombre de couleurs pour colorier une carte donnée, il faut d'abord vérifier si 2 couleurs suffisent. Il est possible de le faire de manière efficace.
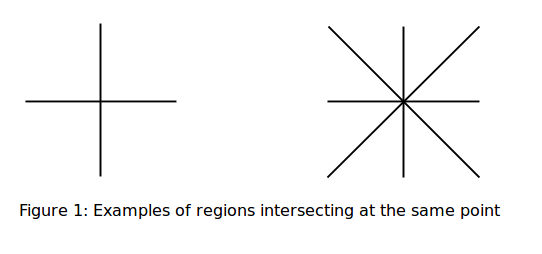
Si on n’utilise que deux couleurs A et B et une région est déjà coloriée, alors on fait le tour du point d’intersection pour fixer la couleur de toutes les régions restantes :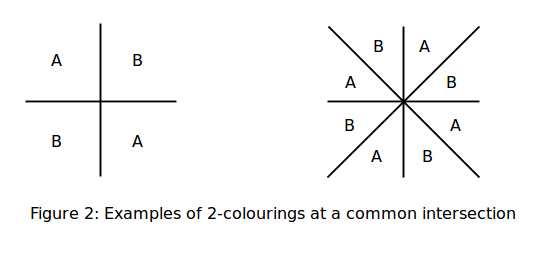
Cette règle est également utile pour un premier essai de coloration des cartes qui nécessitent 3 ou 4 couleurs. Par exemple, si la région 1 ci-dessous a déjà reçu la couleur A, les régions 2 et 4 doivent recevoir une couleur différente mais pour l’instant inconnue. Mais nous savons que colorer la région 3 avec la couleur A ne pose aucune restriction supplémentaire sur les régions 2 et 4 car elles sont déjà adjacentes à une région de couleur A.
La figure 3 n’affiche qu'une petite partie de la carte, mais on peut affiner l'heuristique ci-dessus pour n’importe quelle carte. Si tous les voisins de la région 3 (dans figure 3, les régions 2 et 4) ont au moins un voisin de couleur A (dans figure 3, la région 1), alors il est impossible que colorier la région 3 avec la couleur A soit une erreur. Ceci s’explique par le fait que la coloration de la région 3 avec la couleur A ne pose aucune nouvelle restriction sur ses voisins; ils sont déjà interdits d'avoir la couleur A. Donc, si en poursuivant la coloration il s’avère qu’on a commis une erreur (le nombre de couleurs ne suffit pas), il n’y aura aucun intérêt à recolorier la région 3, c’est un autre choix de couleur qui est erronée. - Que faut-il faire si la région 3 ci-dessus est également le voisin diagonal d’une autre région, disons la région 9, déjà coloriée avec une autre couleur telle que B? Faut-il colorier 3 avec A ou B? Ici, il serait utile de vérifier si les voisins de la région 3 soient interdits d’avoir la couleur A ou la couleur B. Si ni l’une ni l’autre est interdite, il vaut mieux attendre pour colorier la 3.






Suivez ou abonnez-vous à l'Infolettre