300000
English | Français | فارسی | 中文 | Українська | Azerbaijani | ខ្មែរ | Tiếng Việt | Bahasa Melayu | Deutsch | O'zbek | Русскийسیل رنگ‌ها©
تعداد بردها: 209822
راهنمای بازی « سیل رنگ‌ها »
مساله استفاده از کمترین تعداد رنگ برای رنگ کردن نقشه، بر اساس توضیحات ارائه شده، تاریخ طولانی دارد، به عنوان مثال، در یک مقاله ویکی پدیا. این قضیه کهیک نقشه ساده را همیشه می‌توان با 4 رنگ مختلف، رنگ‌آمیزی رنگ کرد به عنوان اولین قضیه بزرگ ریاضی معروف شد و فقط توسط رایانه‌ها ثابت شده است و بوسیله ارائه یک برهان ریاضی توسط ریاضیدانان.
هیچ الگوریتم شناخته شده‌ای برای بهینه رنگ کردن نقشه وجود ندارد. منظور از "بهینه" این است که اگر تعداد ناحیه‌ها ، N ، عدد بزرگی باشد، آنگاه تعداد انتخاب‌های لازم برای رنگ‌آمیزی به صورت Nk رشد می‌کند که در آن k عددی است که به N بستگی ندارد. به بیان دیگر، برای الگوریتم های «بهینه»، تعداد انتخاب‌ها مثل یک چندجمله‌ای از درجه N رشد می‌کند. در عوض، الگوریتم‌های رنگ‌آمیزی شناخته شده یک پیچیدگی توانی دارند، یعنی تعداد انتخاب‌ها به N با رابطه ۴N بستگی دارد.
گر استفاده از 5 یا 6 رنگ مجاز باشد، یا نقشه فقط به دو رنگ نیاز داشته باشد، الگوریتم‌های بهینه شناخته شده‌اند.
امکان دیگر برای رسیدن به روش بهینه این است که، توقع نداشته باشیم که الگوریتم همیشه بهینه باشد. ابتکارهایی (یعنی مجموعه دستورالعمل‌ها) که حداقل در بیشتر موارد قابل به کارگیری هستند در ادامه مطرح می‌شوند :
سوال اول. کدام ناحیه باید زودتر رنگ شود؟
- بهتر است که در ابتدا، ناحیه‌ای رنگ شود که بیشترین مجاور را دارد. به این دلیل که اگر آن ناحیه با رنگ A رنگ‌آمیزی شود آنگاه هیچیک از مجاورها نمیتوانند با رنگ A رنگ‌آمیزی شوند. این موضوع تعداد انتخاب‌های رنگ را برای ناحیه‌های مجاور و بنابر این، تعداد انتخاب‌های بعدی، در شرایطی که رنگ‌آمیزی دشوار باشد را کاهش می‌دهد.
سوال دوم. چه انتخابی از رنگ‌ها آزاد است؟
- رنگی که در اولین رنگ‌آمیزی استفاده میشود قطعا آزاد است.
- اولین باری که از رنگ دوم برای رنگ کردن یک ناحیه استفاده میشود این انتخاب رنگ آزاد است. اگر این ناحیه در همسایگی ناحیه‌ای باشد که در ابتدا رنگ شده است، یعنی اگر رنگ دوم لازم باشد.
- اولین باری که رنگ سوم برای رنگ کردن یک ناحیه استفاده میشود، این انتخاب رنگ آزاد است اگر این ناحیه در همسایگی ناحیههایی باشد که با رنگ اول یا رنگ دوم رنگ‌آمیزی شده‌اند، یعنی اگر رنگ سوم لازم باشد.
سوال سوم. کدام ناحیه در مرحله بعدی باید رنگ شود؟
- در مرحله بعدی ناحیه‌ای را رنگ می‌کنیم که برای آن فقط یک رنگ مجاز باقی مانده باشد به گونه‌ای که نتوانیم اشتباهی در این رنگ‌آمیزی داشته باشیم.
- تعداد تلاش‌های رنگ‌آمیزی قطعاً کمتر از 4N است (آزمایش هر 4 رنگ برای همه مناطق N). بنابراین این تعداد تلاش برای رنگ‌آمیزی به شدت به تعداد مناطق N بستگی دارد. در نتیجه، مفید است اگر یک رنگ‌آمیزی قسمت سفید (بدون رنگ) نقشه را به نقشه‌های فرعی سفید جدا شده جداگانه تقسیم کند که می‌توانند خود به خود رنگ شوند. این مناطق فقط N1 و N2 منطقه دارند (N = N1 + N2)، که اکنون حداکثر به 4N1 + 4N2 نیاز دارند که بسیار کمتر از 4N1 × 4N2 = 4N تلاش.
- >اگر کسی می‌خواهد که کمترین تعداد رنگ‌های لازم برای رنگ کردن یک نقشه داده شده را پیدا کند آنگاه می‌تواند در ابتدا بررسی کند که آیا ۲ رنگ کافی است. این کار می‌تواند به صورت بهینه انجام شود.
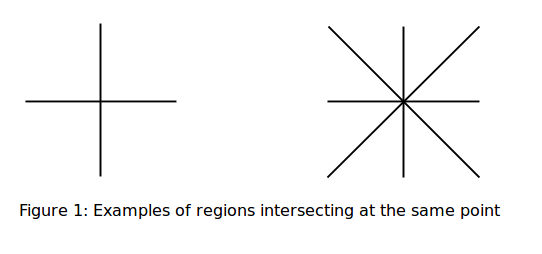
اگر قرار باشد که فقط از دو رنگ A و B استفاده شوند و یکی از ناحیه‌ها رنگ‌آمیزی شده باشد، آنگاه با یررسی قسمت‌های مشترک، رنگ سایر ناحیه‌ها را مشخص می‌کند :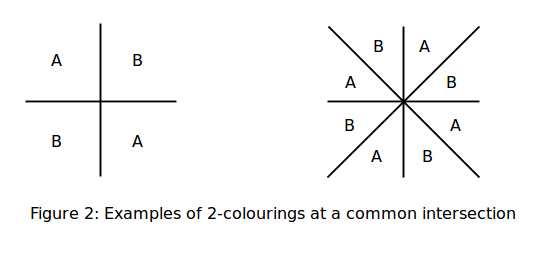
این قانون همچنین برای اولین انتخاب رنگ‌آمیزی یک نقشه که به ۳ یا ۴ رنگ نیاز دارد مفید است. به عنوان مثال، اگر ناحیه ۱ در نقشه زیر با رنگ A رنگ‌آمیزی شده باشد، آنگاه ناحیه‌های۲ و ۴ به رنگ‌های متفاوتی نیاز دارند و ما هیچ ایده‌ای نداریم که آن رنگ چه خواهد بود اما می‌دانیم که رنگ کردن ناحیه ۳ با رنگ A محدودیت بیشتری برای رنگ‌آمیزی ناحیه‌های ۲ و ۴ اعمال نمی‌کند، چرا که آنها قبلا در مجاورت ناحیه‌ای با رنگ A قرار گرفته‌اند.
شکل ۳ فقط بخش کوچکی از نقشه را نشان می‌دهد اما روش فوق می‌تواند به شکل دقیق‌تری برای هر نقشه‌ای استفاده شود. اگر همه مجاورهای ناحیه ۳ (در شکل ۳، ناحیه‌ها۲ و ۴) حداقل یک مجاور با رنگ A دارند (در شکل ۳، ناحیه ۱)، رنگ کردن ناحیه ۳ با رنگ A نمی‌تواند اشتباه باشد. دلیل آن این است که رنگ کردن ناحیه ۳ با رنگ (الف) هیچ محدودیت جدیدی برای مجاورهای آن به وجود نمی‌آورد، چرا که آنها از پیش از داشتن رنگ A ممنوع شده‌اند. بنابر این، اگر رنگ‌آمیزی‌های بعدی مشخص شود که اشتباهی رخ داده است (به این دلیل که تعداد رنگ‌ها کافی نیست)، آنگاه هیچ امتیازی در اینکه برای ناحیه ۳ رنگی غیر از A در نظر گرفته شود وجود ندارد، رنگ‌آمیزی های دیگری باید دوباره امتحان شوند. - اگر ناحیه ۳ در بالا، به صورت قطری مجاور ناحیه دیگری باشد چه اتفاقی می‌افتد، برای مثال، ناحیه ۹ که از قبل رنگ دیگری دارد، مثلا رنگ B؟ آیا ۳ باید به رنگ A یا B رنگ شود؟ همچنین اینجا بررسی همه مجاورهای ۳ کمک کننده است. زیرا آنها از قبل از داشتن رنگ A یا B محروم شده‌اند. اگر هیچ یک از این موارد نباشد ، آنگاه ما می‌توانیم تا رنگ‌آمیزی ۳ منتظر بمانیم.
برای به روز رسانی عضو شوید و یا ما را دنبال کنید: