Floodfill ©

Caribou in Covid: Contests are running online as usual. Check out the FAQ for further questions.

300000

400102

202059

Floodfill^©

A Guide for Playing Floodfill

The problem of using a minimal number of colours to colour a map has a long history as explained, for example, in the Wikipedia article https://en.wikipedia.org/wiki/Four_color_theorem. The theorem that 4 colours are always enough to colour a plane map became famous as the first big mathematical theorem that could be proven only by computer and not through a human produced 'mathematical' proof.

There is no algorithm known that always colours maps efficiently. With 'efficiently' we mean that if the number of regions N is very large then the number of necessary colouring attempts grows only like N^k where k is a number that does not depend on N. In other words, for 'efficient' algorithms the number of attempts grows only like a polynomial of N. Instead, known colouring algorithms have a so-called exponential complexity, i.e. the number of tries depends on N like 4^N.

If one were allowed to use 5 or 6 colours, or if the map needs only 2 colours, then efficient algorithms are known.

Another opportunity to get an efficient method is to drop the requirement that the algorithm is ALWAYS efficient. Such a heuristic (i.e. a set of instructions) that works at least in many cases is to be discussed below:

Q. Which region should be colored first?

Q. Which choice of colours is free?

Q. Which region should be coloured next?

We should colour a region next for which there is only one possible colour left so that we can not make a mistake in this colouring.
The number of colouring attempts is definitely less than 4^N (trying all 4 colours for all N regions). So this number of colouring attempts depends critically on the number of regions N. Consequently it is useful if a colouring splits the white (uncoloured) part of the map into separate disconnected white sub-maps which then can be coloured on their own. These regions have only N₁ and N₂ regions (N = N₁ + N₂), needing now at most only 4^N₁ + 4^N₂ tries which is much less than 4^N₁ × 4^N₂ = 4^N tries.
If one wants to find the smallest number of colours that can colour a given map then one first has to check whether 2 colours are enough. This can be done efficiently.

If only two colours A and B are to be used and one of the regions already has a colour, then going around the point of intersection fixes the colour of all other regions:

This rule is also useful for a first colouring attempt of maps that need 3 or 4 colours. For example, if region 1 below has already colour A then regions 2 and 4 need a different colour and we have no idea what that could be but we know that colouring region 3 with colour A does not pose extra conditions on the colouring of regions 2 and 4, because they already have a neighbour of colour A.

Figure 3 shows only a small part of the map but the above heuristic can be made more precise for any map. If all neighbours of region 3 (in Figure 3, regions 2 and 4) have at least one neighbour of colour A (in Figure 3, region 1), then colouring region 3 with colour A can not be a mistake. The reason is that colouring region 3 with A does not create any new restriction on its neighbours because they are already forbidden to have colour A. So if in the further colouring process it turns out that a mistake has been made (because the number of colours is not enough), then there is no point in giving region 3 a different colour than A, some other colouring must be re-tried.
What if region 3 above is also a diagonal neighbour to another region, say region 9, which already has a different colour, like colour B? Should 3 be coloured with A or B? Also here it helps to check all neighbours of 3 whether they are already forbidden to have colour A or forbidden to have colour B. If neither is the case then we might wait with colouring 3.

Un Guide pour Jouer à Floodfill

Utiliser un nombre minimal de couleurs pour colorier une carte est un problème dont l’histoire est longue, tel qu’en témoigne l'article de Wikipédia sur Le Théorème des Quatre Couleurs. Le théorème que 4 couleurs suffisent toujours pour colorier une carte plane est devenu célèbre en tant que le premier grand théorème mathématique qui exigeait une démonstration mathématique par ordinateur plutôt que par un humain.

Il n’existe aucun algorithme connu de nos jours qui colorie les cartes de manière efficace. Par « efficace » on entend que si le nombre de régions N est très grand, alors le nombre d’essais de coloriage augmente selon N^k où k est un nombre qui ne dépend pas de N. Autrement dit, pour un algorithme « efficace », le nombre d’essais augmente selon un polynôme de N. Or, les algorithmes de coloration ont une complexité exponentielle. C'est-à-dire, le nombre d’essais dépend de N comme 4^N.

Si on permet l’utilisation de cinq ou six couleurs, ou si la carte ne nécessite que 2 couleurs, alors des algorithmes efficaces sont connus.

Une autre occasion d'obtenir une méthode efficace est de ne plus exiger que l'algorithme soit TOUJOURS efficace. On décrit ci-dessous une telle heuristique (ou un ensemble d'instructions) qui fonctionne, au moins, dans un bon nombre de cas:

Q. Quelle région faut-il colorier en premier?

Q. Quel choix de couleur est sans restriction?

Q. Quelle région devrait-on colorier ensuite?

La prochaine région à colorier est celle où il ne reste qu’une seule couleur à choisir, de sorte qu’il est impossible de se tromper. Le nombre d’essais de coloration est certainement inférieur à 4^N (en essayant toutes les 4 couleurs pour toutes les N régions). Alors le nombre d’essais de coloration dépend du nombre de régions N. Par conséquent, il est utile de colorier une région qui divise la partie blanche (incolore) de la carte en de petites mini-cartes séparées qu’on peut ensuite colorier individuellement. Ces régions se composent de N₁ et N₂ régions (N = N₁ + N₂) seulement. En plus, il ne faut maintenant qu’au plus 4^N₁ + 4^N₂ essais, ce qui est bien inférieur à 4^N₁ × 4^N₂ = 4^N essais.
Si on veut trouver le plus petit nombre de couleurs pour colorier une carte donnée, il faut d'abord vérifier si 2 couleurs suffisent. Il est possible de le faire de manière efficace.

Si on n’utilise que deux couleurs A et B et une région est déjà coloriée, alors on fait le tour du point d’intersection pour fixer la couleur de toutes les régions restantes :

Cette règle est également utile pour un premier essai de coloration des cartes qui nécessitent 3 ou 4 couleurs. Par exemple, si la région 1 ci-dessous a déjà reçu la couleur A, les régions 2 et 4 doivent recevoir une couleur différente mais pour l’instant inconnue. Mais nous savons que colorer la région 3 avec la couleur A ne pose aucune restriction supplémentaire sur les régions 2 et 4 car elles sont déjà adjacentes à une région de couleur A.

La figure 3 n’affiche qu'une petite partie de la carte, mais on peut affiner l'heuristique ci-dessus pour n’importe quelle carte. Si tous les voisins de la région 3 (dans figure 3, les régions 2 et 4) ont au moins un voisin de couleur A (dans figure 3, la région 1), alors il est impossible que colorier la région 3 avec la couleur A soit une erreur. Ceci s’explique par le fait que la coloration de la région 3 avec la couleur A ne pose aucune nouvelle restriction sur ses voisins; ils sont déjà interdits d'avoir la couleur A. Donc, si en poursuivant la coloration il s’avère qu’on a commis une erreur (le nombre de couleurs ne suffit pas), il n’y aura aucun intérêt à recolorier la région 3, c’est un autre choix de couleur qui est erronée.
Que faut-il faire si la région 3 ci-dessus est également le voisin diagonal d’une autre région, disons la région 9, déjà coloriée avec une autre couleur telle que B? Faut-il colorier 3 avec A ou B? Ici, il serait utile de vérifier si les voisins de la région 3 soient interdits d’avoir la couleur A ou la couleur B. Si ni l’une ni l’autre est interdite, il vaut mieux attendre pour colorier la 3.

填色游戏指南

正如所介绍的，用最少的颜色来填充一个地图的问题具有很长的历史，比如，在维基百科的文章中https://en.wikipedia.org/wiki/Four_color_theorem.仅用4个颜色就可以填涂一个空白地图的定理是一个有名的只能运用电脑证明而不能被人类计算所证明的头号数学定理。

没有已知算法可以每次都有效率地填涂地图。所谓有效率即指如果有N个很大的区域，那么需要的填色尝试次数只以 N^k增长，k并不取决于N.换句话说，在最有效率的算法中尝试的次数应只以N的多项式增长。然而，已知的填色算法有所谓的指数复杂性，换句话说，填色尝试次数取决于N，比如4^N。.

如果可以使用5或6个颜色，或者如果地图只需要两个颜色，最有效率的算法是已知的。

另一个得到最有效率的方法的机会是放弃任何情况下都最有效率这一要求。至少在多数情况下有效的这种探索性步骤（换句话说，一组指令）会在下面进行讨论：

Q.哪个区域应该先被填色？

Q.哪一种颜色选择不受限制？

Q.哪一个区域应该下一个被涂色？

下一个要涂的区域应该只有一种可涂颜色，这样我们就不会在涂色上出错。
涂色的尝试应小于4^N次（对于N个区域的每一个都尝试所有的4种颜色）。所以涂色的尝试次数很大程度上取决于区域的个数N。所以，如果填色后地图的白色（未填涂的）部分被分成了单独而不相邻的，而且后续可被自行填涂的白色子地图，将会很有用。这些区域只有N^1和N^2个部分(N = N^1 + N^2)，现在最多只需要4^N1 + 4^N2次尝试，这比4^N1 * 4^N2 = 4^N次尝试要少得多。
如果想要找到填涂一个已知的地图最少的使用的颜色个数，必须先检查2个颜色是否足够。这可以有效率地完成。

如果只有两种颜色A和B可以使用并且其中一个区域已经被涂上一种颜色，那么在交点附近检查可以确定其它所有区域的颜色：

这个规则对于需要用3或4种颜色填涂的首次尝试的地图也适用。例如，如果下方区域1已经有颜色A那么区域2和4需要不同的颜色，我们并不知道有可能是那种颜色但我们知道用颜色A填涂区域3不会影响填涂区域2和4的条件，因为它们已经有相邻的颜色A。

图3只显示了地图的一小部分但是上方的探索性步骤对于任何地图都可以变得更加精准。如果区域3的所有邻近区域（在图3中，区域2和4）都至少有一个相邻的区域被涂上颜色A（在图3中，区域1），那么用颜色A涂区域3不会出错。这是因为这样做不会为其相邻区域带来限制，因为这些区域已经不能使用颜色A。所以如果在后续涂色过程发现了错误（因为颜色的个数不足），区域3也不会有除了A外的其它选择，应该尝试在其它涂色步骤中更改颜色。
如果区域3的上方也有一个对角相邻的区域，比如有颜色B的区域9，这会怎么样呢？区域3应该用A或B着色吗？在这里，检查所有3的邻接区域是否已经不可用颜色A或者颜色B将十分有帮助。如果两种情况都不对那么我们可先不涂3.

ការណែនាំសម្រាប់ការលេងហ្គេម Floodfill

បញ្ហានៃការប្រើចំនួនពណ៌តិចបំផុតដើម្បីដាក់ពណ៌លើផែនទី មានប្រវត្តិយូរយារណាស់មកហើយដូចដែលបានពន្យល់ ជាឧទាហរណ៍នៅក្នុងអត្ថបទវិគីភីឌា ទ្រឹស្តីបទដែលថា ៤ ពណ៌គឺគ្រប់គ្រាន់សម្រាប់ដាក់ពណ៌ប្លង់ផែនទីបានក្លាយជាល្បីល្បាញដោយសារជាទ្រឹស្តីបទគណិតវិទ្យាធំដំបូងគេបង្អស់ដែលអាចស្រាយបញ្ជាក់បានតែតាមរយៈកុំព្យូទ័រប៉ុណ្ណោះ មិនមែនតាមរយៈសម្រាយបញ្ជាក់គណិតវិទ្យាដែលមនុស្សផលិតឡើយ។

គេមិនទាន់ដឹងក្បួនដោះស្រាយច្បាស់លាស់ដើម្បីដាក់ពណ៌ផែនទីប្រកបដោយប្រសិទ្ធភាពនៅឡើយទេ។ ជាមួយពាក្យ 'ប្រកបដោយប្រសិទ្ធភាព' យើងមានន័យថា ប្រសិនបើចំនួនតំបន់ N មានទំហំធំខ្លាំងនោះចំនួននៃការព្យាយាមលាបពណ៌ចាំបាច់នឹងកើនឡើងដូច N^k ដែល k គឺ ជាចំនួនដែលមិនអាស្រ័យលើ N។ និយាយម្យ៉ាងទៀត សម្រាប់ក្បួនដោះស្រាយដែលមានប្រសិទ្ធភាព ចំនួននៃការប៉ុនប៉ងមានចំនួនកើនឡើងតាមពហុធានៃ N។ ជាងនេះទៅទៀត ក្បួនដោះស្រាយការដាក់ពណ៌ត្រូវបានគេហៅថា exponential complexity ជាឧទាហរណ៍ ចំនួននៃការព្យាយាមអាស្រ័យលើ N ឧទាហរណ៍ដូចជា 4^N ។

ប្រសិនបើគេត្រូវបានអនុញ្ញាតឱ្យប្រើ ៥ ឬ ៦ ពណ៌ ឬប្រសិនបើផែនទីត្រូវការតែ ២ ពណ៌ នោះក្បួនដោះស្រាយដែលមានប្រសិទ្ធភាពនឹងត្រូវបានគេដឹង។

ឱកាសមួយទៀតដើម្បីទទួលបានវិធីសាស្ត្រមានប្រសិទ្ធភាពគឺត្រូវពិភាក្សានិងអនុវត្តតាមក្បួនដោះស្រាយដ៏មានប្រសិទ្ធិភាពមួយ។ វិធីសាស្រ្ត (ជាការណែនាំ) ដែលមានប្រសិទ្ធភាពលើករណីជាច្រើននឹងត្រូវពិភាក្សាដូចខាងក្រោម៖

សំណួរ៖ តើតំបន់ណាដែលត្រូវលាបពណ៌មុនគេ?

សំណួរ៖ តើជម្រើសពណ៌មួយណាដែលរើសបានតាមចិត្ត?

សំណួរ៖ តើត្រូវដាក់ពណ៌តំបន់ណាបន្ទាប់?

តំបន់បន្ទាប់ដែលយើងគួរដាក់ពណ៌គឺតំបន់ដែលនៅសល់ពណ៌តែមួយពណ៌គត់ដែលអាចដាក់បាន ដូចនេះយើងមិនត្រូវមានកំហុសក្នុងការដាក់ពណ៌តំបន់នេះទេ។ .
ចំនួននៃការប៉ុនប៉ងដាក់ពណ៌គឺពិតជាតិចជាង 4^N (បើសាកល្បងដាក់ពណ៌ទាំង ៤ សម្រាប់តំបន់ N នីមួយៗ)។ ដូច្នេះចំនួននៃការប៉ុនប៉ងលាបពណ៌នេះពឹងផ្អែកយ៉ាងសំខាន់ទៅលើចំនួនតំបន់ N។ ហេតុដូច្នេះ វាមានប្រយោជន៍ប្រសិនបើតំបន់ដែលដាក់ពណ៌ញែកតំបន់ពណ៌ស (មិនទាន់ដាក់ពណ៌) ជាផែ្នកផ្សេងៗដែលមិនជាប់គ្នា ដែលធ្វើឲ្យតំបន់ពណ៌សនោះអាចត្រូវបានដាក់ពណ៌ដោយខ្លួនឯង។
ប្រសិនបើអ្នកចង់រកចំនួនពណ៌តិចបំផុតដែលអាចដាក់ពណ៌លើផែនទីដែលឲ្យ នោះដំបូងអ្នកត្រូវពិនិត្យមើលចំនួន ២ ពណ៌ជាការគ្រប់គ្រាន់។ នេះអាចត្រូវបានធ្វើយ៉ាងមានប្រសិទ្ធិភាព។

ប្រសិនបើមានតែពីរពណ៌ A និង B ដែលត្រូវដាក់ តែតំបន់នោះមានពណ៌រួចហើយខុសពីពណ៌ដែលត្រូវដាក់ នោះគេត្រូវជួសជុល(ដាក់ពណ៌សារថ្មី)ចាប់ផ្តើមចេញពីជុំវិញចំនុចប្រសព្វ៖

វិធាននេះក៏មានប្រយោជន៍ចំពោះផែនទីដែលត្រូវប្រើ ៣ ពណ៌ ឬ ៤ ពណ៌ ដែរ ។ ឧទាហរណ៍ ប្រសិនបើតំបន់ទី ១ ខាងក្រោមបានដាក់ពណ៌ A នោះតំបន់ទី ២ និង ទី៤ ត្រូវតែដាក់ពណ៌ផ្សេង ហើយយើងមិនទាន់ដឹងថាត្រូវដាក់ពណ៌ណានៅឡើយទេ ប៉ុន្តែយើងដឹងថាការដាក់ពណ៌ A លើតំបន់ទី ៣ មិនបង្កលក្ខខណ្ឌបន្ថែមលើការដាក់ពណ៌តំបន់ទី ២ និងទី ៤ ទេ ពីព្រោះពួកវាសុទ្ធតែមានតំបន់ជិតខាងដែលមានពណ៌ A រួចហើយ។

រូបភាពទី ៣ បង្ហាញតែផ្នែកតូចមួយនៃផែនទីប៉ុណ្ណោះ ប៉ុន្តែវាអាចធ្វើឱ្យយល់ច្បាស់ដែលអាចយកទៅអនុវត្តសម្រាប់ផែនទីផ្សេងជាច្រើនទៀត។ ប្រសិនបើតំបន់ជិតខាងទាំងអស់នៃតំបន់ទី ៣ (តំបន់ទី ២ និងទី ៤ ក្នុងរូបភាពទី ៣) ក្នុងចំណោមនេះបើវាមានតំបន់ជិតខាងយ់ាងតិចមួយដែលមានពណ៌A (តំបន់ ១ នៅក្នុងរូបភាពទី ៣) នោះការដាក់ពណ៌ A លើតំបន់ទីដែរ មិនអាចជាកំហុសទេ។ មូលហេតុគឺថា ការដាក់ពណ៌ A លើតំបន់ពណ៌ទី ៣ មិនបង្កើតការរឹតត្បិតថ្មីលើតំបន់ជិតខាងទេពីព្រោះពួកគេត្រូវបានហាមឃាត់មិនឱ្យមានពណ៌ A រួចទៅហើយ។ ដូច្នេះ ប្រសិនបើនៅក្នុងដំណើរការដាក់ពណ៌បន្តបន្ទាប់ទៀត បង្ហាញឲ្យឃើញថាមានកំហុស (ដោយសារពណ៌ដែលត្រូវដាក់ជាន់ជាមួយពណ៌នៃតំបន់ជិតខាង) នោះគេត្រូវសាកល្បងដាក់ពណ៌ផ្សេងលើតំបន់ទី ៣ ជំនួសពណ៌ A វិញ។
ចុះបើតំបន់ទី ៣ ខាងលើក៏ជាតំបន់ជិតខាងតាមទិសអង្កត់ទ្រូងទៅនឹងតំបន់ផ្សេងទៀតដែរ ឧទាហរណ៍តំបន់ទី ៩ ដែលមានពណ៌ផ្សេងរួចទៅហើយ ឧទាហរណ៍ដូចជាពណ៌ B នោះតើតំបន់ទី ៣ គួរតែដាក់ពណ៌ A ឬ ពណ៌B? ដូចគ្នានេះដែរ គេត្រូវពិនិត្យមើលតំបន់ជិតខាងទាំងអស់របស់តំបន់ទី ៣ ថាតើពួកគេត្រូវបានហាមឃាត់មិនឱ្យដាក់ពណ៌ A ឬក៏ហាមឃាត់មិនឱ្យមានពណ៌ B ។ ប្រសិនបើមិនចូលករណីណាមួយនោះទេ ការដាក់ពណ៌លើតំបន់ទី៣ អាចត្រូវរង់ចាំសិន (ដាក់ពណ៌កន្លែងផ្សេងសិន) ។

A Guide for Playing Floodfill

مشکل استفاده از کمترین تعداد رنگ برای رنگ کردن نقشه، بر اساس توضیحات ارائه شده، تاریخ طولانی دارد، به عنوان مثال، در یک مقاله ی ویکی پدیا https://fa.wikipedia.org/wiki/%D9%82%D8%B6%DB%8C%D9%87_%DA%86%D9%87%D8%A7%D8%B1%D8%B1%D9%86%DA%AF. این قضیه که 4 رنگ همیشه کافی است که یک نقشه ی ساده را رنگ کرد به عنوان اولین قضیه ی ریاضی بزرگ معروف شد که فقط می توانست توسط رایانه ثابت شود و نه توسط اثبات ریاضی تولید شده توسط انسان.

هیچ الگوریتم شناخته شده ای برای بهینه رنگ کردن نقشه وجود ندارد. منظور از "بهینه" این است که اگر تعداد نواحی N عدد بزرگی است، آنگاه تعداد تلاش های لازم برای رنگ کردن مثل N^k رشد می کندکه در آن k عددی است که به N بستگی ندارد. به بیان دیگر، برای الگوریتم های "بهینه"، تعداد تلاش ها مثل یک چند جمله ای از N رشد می کند. در عوض، الگوریتم های رنگ آمیزی شناخته شده یک پیچیدگی توانی دارند، یعنی تعداد تلاش ها به N با رابطه ی ۴^N بستگی دارد.

اگر استفاده از 5 یا 6 رنگ مجاز باشد، یا نقشه فقط دو رنگ نیاز داشته باشد، الگوریتم های بهینه شناخته شده اند.

فرصتی دیگر برای رسیدن به روش بهینه این است که، اینکه الگوریتم همیشه بهینه است، کنار گذاشته شود. همچین ابتکاری (یعنی مجموعه ی دستورالعمل ها) که حداقل در بیشتر موارد قابل به کار گیری است باید ذیل مطرح شود:

سوال اول. کدام ناحیه باید اول رنگ شود؟

سوال دوم. چه انتخابی از رنگها آزاد است؟

سوال سوم. کدام ناحیه در مرحله بعدی باید رنگ شود؟

در مرحله ی بعدی ناحیه ای را رنگ کنیم که برای آن فقط یک رنگ محتمل باقی مانده باشد به گونه ای که نتوانیم اشتباهی در این رنگ آمیزی داشته باشیم.
تعداد تلاش ها برای رنگ آمیزی قطعا کمتر از ۴^N (امتحان کردن همه ی ۴ رنگ برای همه ی N ناحیه). بنابراین این تعداد تلاش ها برای رنگ آمیزی به صورت مهمی بستگی به تعداد ناحیه ها N دارد. در نتیجه این مفید خواهدبود که رنگ آمیزی قسمت سفید (رنگ نشده) نقشه را به زیر نقشه های غیر متصل جدا از هم که بعدا می توانند جداگانه رنگ شوند، تقسیم کرد. این نواحی فقط N_۱ و N_۲ ناحیه دارند (=N_۱+N_۲ N) ، که نیاز به حداکثر ۴^{(N_۱ )}+۴^{(N_۲ )}=۴^N تلاش دارد که بسیار کمتر از ۴^{(N_۱ )}*۴^{(N_۲ )}=۴^N تلاش است.
اگر کسی می خواهد که کمترین تعداد رنگ های لازم برای رنگ کردن یک نقشه ی داده شده را پیدا کند آنگاه می تواند در ابتدا بررسی کند که آیا ۲ رنگ کافی است. این کار می تواند به صورت بهینه انجام شود.

اگر فقط دو رنگ (الف) و (ب) قرار باشد که استفاده شوند و یکی از نواحی رنگ آمیزی شده باشد، آنگاه چرخیدن پیرامون نقطه ی اشتراک، رنگ سایر نواحی را تنظیم می کند:

این قانون همچنین برای اولین تلاش رنگ آمیزی نقشه مفید است که ۳ یا ۴ لازم دارد. به عنوان مثال، اگر ناحیه ی ۱ در زیر به رنگ (الف) رنگ آمیزی شده، آنگاه نواحی ۲ و ۴ رنگ های متفاوتی نیاز دارندو ما هیچ ایده ای نداریم که آن رنگ چه خواهد بود اما می دانیم که رنگ کردن ناحیه ی ۳ با رنگ (الف) شرایط بیشتری بر رنگ آمیزی نواحی ۲ و ۴ اعمال نمی کند، چرا که آنها از پیش در همسایگی ناحیه ای با رنگ (الف) قرار گرفته اند.

شکل ۳ فقط یهک بخش کوچکی از نقشه را نشان می دهد اما روش فوق می تواند به شکل دقیق تری برای هر نقشه ای استفاده شود. اگر همه ی همسایه های ناحیه ی ۳ (در شکل ۳، نواحی ۲ و ۴) حداقل یک همسایه با رنگ (الف) دارند (در شکل ۳، ناحیه ی ۱)، رنگ کردن ناحیه ی ۳ با رنگ (الف) نمی تواند اشتباه باشد. دلیل آن این است که رنگ کردن ناحیه ی ۳ با رنگ (الف) هیچ محدودیت جدیدی برای همسایه های آن به وجود نمی آورد، چرا که آنها از پیش از داشتن رنگ (الف) ممنوع شده اند. بنابراین اگر رنگ آمیزی های بعدی مشخص شود که اشتباهی رخ داده است (به این دلیل که تعداد رنگ ها کافی نیست)، آنگاه هیچ امتیازی در اینکه برای ناحیه ی ۳ رنگی غیر از (الف) در نظر گرفته شود وجود ندارد، رنگ آمیزی های های دیگری باید دوباره امتحان شوند.
چه می شود اگر ناحیه ی ۳ در بالا، به صورت قطری همسایه ی ناحیه ی دیگری باشد، مثلا ناحیه ی ۹، که از پیش رنگ دیگری دارد، مثلا رنگ (ب)؟ آیا ۳ باید به رنگ (الف) یا (ب) رنگ شود؟ همچنین اینجا چک کردن همه ی همسایه های ۳ کمک کننده است چه آنها از پیش از داشتن رنگ (الف) یا (ب) ممنوع شده باشند. اگر هیچ یک از این موارد نباشد آنگاه ما می توانیم با رنگ آمیزی ۳ منتظر بمانیم.

Hướng dẫn chơi trò Floodfill

Việc sử dụng số lượng màu sắc ít nhất có thể để tô màu bản đồ có lịch sử lâu đời như đã giải thích, ví dụ như trong bài viết trên Wikipedia https://en.wikipedia.org/wiki/Four_color_theorem. Định lý rằng 4 màu luôn là đủ để tô màu một bản đồ mặt phẳng đã trở nên nổi tiếng như một định lý toán học lớn đầu tiên chỉ có thể được chứng minh bằng máy tính mà không phải thông qua một bằng chứng 'toán học' do con người tạo ra.

Không có thuật toán nào được biết là sẽ luôn tô màu bản đồ một cách hiệu quả. 'Hiệu quả' ở đây có nghĩa là nếu số vùng N rất lớn thì số lần tô màu cần thiết chỉ tăng lên giống như N^k trong đó k là số không phụ thuộc vào N. Nói cách khác, đối với các thuật toán 'hiệu quả', số lần thử chỉ tăng lên giống như một đa thức của N. Thay vào đó, các thuật toán tô màu hiện có cái gọi là độ phức tạp theo cấp số nhân, tức là số lần thử phụ thuộc vào N như 4^N.

Nếu một người được phép sử dụng 5 hoặc 6 màu, hoặc nếu bản đồ chỉ cần 2 màu, thì các thuật toán hiệu quả được công nhận.

Một cơ hội khác để có được một phương pháp hiệu quả là loại bỏ yêu cầu rằng thuật toán LUÔN LUÔN hiệu quả. Phương pháp heuristic như vậy (tức là một tổ hợp các hướng dẫn) ít nhất có hoạt động trong các trường hợp sẽ được thảo luận dưới đây:

Q. Nên tô màu khu vực nào trước?

Q. Lần tô nào được tự do chọn màu?

Q. Nên tô màu khu vực nào tiếp theo?

Chúng ta nên tô màu cho một vùng tiếp theo khi vùng này chỉ có thể tô một màu duy nhất khả thi để chúng ta không mắc lỗi khi tô màu này.
Số lần thử tô màu luôn ít hơn 4^N (thử cả 4 màu cho tất cả N vùng). Vì vậy, số lần thử tô màu này phụ thuộc rất nhiều vào số vùng N. Do đó, sẽ rất hữu ích nếu việc tô màu chia phần màu trắng (chưa tô màu) của bản đồ thành các bản đồ con màu trắng riêng biệt không kết nối với nhau mà sau đó lại tiếp tục được tô màu theo cách riêng. Những vùng này chỉ có N^1 và N^2 vùng (N = N^1 + N^2), bây giờ chỉ cần nhiều nhất là 4^N1 + 4^N2 lần thử mà rõ ràng là nhỏ hơn nhiều so với 4^N1 * 4^N2 = 4^N lần thử.
Nếu một người muốn tìm số lượng màu tối thiểu để có thể tô màu cho một bản đồ nhất định thì trước tiên người ta phải kiểm tra xem liệu 2 màu có đủ không. Điều này có thể được thực hiện một cách hiệu quả.

Nếu chỉ sử dụng hai màu A và B và một trong số các vùng đã có màu, thì việc di chuyển xung quanh điểm giao nhau sẽ sửa màu của tất cả các vùng khác:

Quy tắc này cũng hữu ích để áp dụng cho lần thử tô màu đầu tiên của bản đồ cần 3 hoặc 4 màu. Ví dụ: nếu vùng 1 bên dưới đã có màu A thì vùng 2 và 4 cần một màu khác và ta không biết đó có thể là màu gì nhưng ta biết rằng việc tô màu vùng 3 với màu A không làm nảy sinh thêm các điều kiện về tô màu của vùng 2 và 4, bởi vì chúng sẵn đã tiếp xúc một vùng lân cận có màu A.

Hình 3 chỉ thể hiện một phần nhỏ của bản đồ tuy nhiên phương pháp heuristic ở trên có thể được thực hiện một cách chính xác đối với bất kỳ bản đồ nào. Nếu tất cả các vùng lân cận của vùng 3 (trong Hình 3, vùng 2 và 4) có ít nhất một vùng lân cận sử dụng màu A (trong Hình 3, vùng 1), thì việc tô màu vùng 3 với màu A sẽ không gây ra lỗi sai nào. Lý do là việc tô màu vùng 3 với màu A không tạo ra bất kỳ hạn chế nào đối với các vùng xung quanh nó bởi vì chúng vốn đã không được sử dụng màu A. Vì vậy, nếu trong quá trình tô màu tiếp theo, cuối cùng lại xảy ra một lỗi sai (vì số lượng màu không đủ), thì việc cho khu vực 3 một màu khác với màu A là vô nghĩa, một số màu khác phải được thay đổi.
Điều gì sẽ xảy ra nếu vùng 3 ở trên cũng là vùng tiếp xúc theo đường chéo của vùng khác, chẳng hạn như vùng 9 đã có một màu khác ví dụ là màu B? Câu hỏi là vùng 3 nên được tô màu A hay B? Ở trường hợp này nó cũng giúp kiểm tra tất cả những vùng xung quanh của 3 xem chúng có bị hạn chế không được tô màu A hay không được tô màu B không. Nếu đều không hạn chế tô màu nào cả thì chúng ta có thể tạm thời chưa vội tô vùng 3.

Panduan untuk Permainan Floodfill

Soalan menggunakan warna yang minimum untuk mewarnai peta memiliki sejarah panjang seperti yang dijelaskan dalam artikel Wikipedia https://en.wikipedia.org/wiki/Four_color_theorem. Teorem mengenai 4 warna selalunya cukup untuk mewarnai satu peta menjadi terkenal sebagai teorem matematik besar pertama yang dapat dibuktikan hanya dengan komputer dan bukan melalui bukti 'mathematical' yang dihasilkan oleh manusia.

Tidak ada algoritma yang diketahui yang selalu mewarnai peta dengan cekap (efficiently). Dengan 'efficiently' kita bermaksud bahawa jika bilangan kawasan N sangat besar maka jumlah percubaan mewarna yang diperlukan hanya muncul seperti N^k di mana k adalah nombor yang tidak bergantung kepada N.

Jika seseorang dibenarkan menggunakan 5 atau 6 warna, atau jika peta hanya memerlukan 2 warna, algoritma yang cekap akan diketahui.

Peluang lain untuk mendapatkan kaedah yang cekap adalah melepaskan syarat bahawa algoritma SELALU cekap. Heuristik seperti itu (iaitu sekumpulan arahan) yang berfungsi sekurang-kurangnya dalam banyak kes akan dibincangkan di bawah:

Q. Kawasan mana yang mesti diwarnakan terlebih dahulu?

Q. Pilihan warna mana adalah bebas?

Q. Kawasan mana perlu diwarnakan seterusnya?

Kita harus mewarnai kawasan seterusnya yang hanya ada satu kemungkinan warna yang tertinggal supaya tidak melakukan kesilapan dalam pewarnaan ini.
Jumlah percubaan mewarna pasti kurang dari 4^N (mencuba semua 4 warna di seluruh kawasan N). Oleh itu, jumlah percubaan pewarnaan ini sangat bergantung pada bilangan kawasan N. Oleh itu, adalah berguna jika pewarnaan pisahkan bahagian putih (tidak berwarna) kepada peta sampingan putih yang terasing yang kemudian boleh diwarnakan sendiri. Kawasan-kawasan ini hanya menpunyai kawasan N^1 dan N^2 (N= N^1 + N^2),memerlukan sekarang paling banyak hanya 4^N1 +4^N2 percubaan yang jauh lebih sedikit daripada 4^N1 * 4^N2 = 4^N mencuba.
Sekiranya seseorang ingin mencari bilangan warna terkecil yang dapat mewarnai peta tertentu, seseorang harus memeriksa terlebih dahulu sama ada 2 warna sudah mencukupi. Ini dapat dilakukan dengan cekap.

Sekiranya hanya dua warna A dan B yang akan digunakan dan salah satu kawasan sudah berwarna, maka mewarnai di sekelliling titik persimpangan akan membetulkan warna semua kawasan lain:

Peraturan ini juga berguna untuk percubaan mewarna peta pertama yang memerlukan 3 atau 4 warna. Sebagai contoh, jika kawasan 1 di bawah sudah berwarna A maka kawasan 2 dan 4 memerlukan warna yang berbeza dan kita tidak tahu tetapi kita tahu bahawa mewarnakan kawasan 3 dengan warna A tidak menimbulkan syarat tambahan pada pewarnaan kawasan 2 dan 4, kerana mereka sudah mempunyai jiran berwarna A.

Rajah 3 menunjukkan hanya sebahaguan kecil peta tetapi heuristik sebelumnya dapat dibuat lebih tepat untuk sebarang peta. Sekiranya semua jiran kawasan 3(dalam Rajah 3, kawasan 2 dan 4)mempunyai sekurang-kurangnya satu jiran berwarna A (dalam Rajah 3, kawasan 1), maka mewarnai kawasan 3 dengan warna A tidak akan menjadi salah. Sebabnya ialah bahawa mewarnai kawasan 3 dengan warna A tidak akan menimbulkan sekatan baru pada jirannya kerana mereka sudah dilarang untuk memiliki warna A. Oleh itu, jika dalam proses pewarnaan selanjutnya menimbulkan kesalahan (kerana jumlah warna tidak cukup), maka tidak ada gunanya memberi kawasan 3 warna yang berbeza daripada A, beberapa pewarna lain mesti dicuba semula.

Bagaimana jika kawasan 3 di atas juga merupakan jiran pepenjuru kepada kawasan lain, katakan kawasan 9, yang sudah mempunyai warna yang berbeza, seperti warna B? Kawasan 3 patut diwarnai A atau B? Ia juga berguna untuk menyemak semua jiran kawasan 3 sama ada mereka dilarang mempunyai warna A atau dilarang mempunyai warna B. Sekiranya tidak berlaku, maka kita mungkin manunggu dengan mewarnai kawasan 3.

Інструкція до гри Заливка

Проблема використання мінімальної кількості кольорів для розфарбування карти має довгу історію, наприклад про це можна почитати у статті на Вікіпедії https://en.wikipedia.org/wiki/Four_color_theorem. Теорема про те, що 4 кольорів завжди достатньо для забарвлення плоскої карти, стала відомою як перша велика математична теорема, яку можна було довести лише за допомогою комп’ютера, а не за допомогою „математичного” доведення, створеного людиною.

Не існує алгоритма, який завжди ефективно розфарбовує карти. Під «ефективно» ми маємо на увазі, що якщо кількість регіонів N дуже велика, то кількість необхідних спроб забарвлення зростає як N^k, де k - число, яке не залежить від N. Іншими словами, для «ефективних» алгоритмів кількість спроб зростає поліноміально. Натомість відомі алгоритми забарвлення мають так звану експоненціальну складність, тобто кількість спроб залежить від N, наприклад, як 4^N.
Якщо дозволити використати 5 або 6 кольорів, на карті, де потрібно лише 2 кольори, то ефективні алгоритми відомі.

Іншою можливістю отримати ефективний метод є відмова від вимоги, що алгоритм ЗАВЖДИ ефективний. Таку евристику (тобто набір інструкцій), яка працює принаймні у багатьох випадках, слід обговорити нижче:

Який регіон слід пофарбувати першим?

Корисно спочатку розфарбувати регіон, який має якомога більше сусідів, оскільки якщо цей регіон отримає колір А, то всі її сусіди матимуть обмеження не отримувати колір А. Це зменшує кількість варіантів вибору кольору для цих сусідніх областей, а отже, зменшує кількість подальших спроб у разі, якщо розфабровування виявиться складним.

Який вибір кольорів вільний?

Колір, використаний при першому фарбуванні, безумовно, вільний.

Перший раз, коли другий колір використовується для фарбування регіону, цей вибір кольору є вільним, якщо цей регіон торкається регіону з першим кольором, тобто якщо потрібен другий колір.

Перший раз, коли третій колір використовується для фарбування регіону, цей вибір кольору є вільним, якщо цей регіон торкається регіону з першим кольором та регіону з другим кольором, тобто якщо необхідний третій колір.

Який регіон слід пофарбувати наступним?

Наступним ми повинні розфарбувати регіон, для якого залишився лише один можливий варіант кольору, щоб ми не помилилися із забарвленням.

Кількість спроб забарвлення, безумовно, менше ніж 4^N (спроба використати всі 4 кольори для всіх N регіонів). Отже, ця кількість спроб забарвлення критично залежить від кількості регіонів N. Отже, корисно, якщо забарвлення розділяє білу (не забарвлену) частину карти на окремі від’єднані білі “підкарти”, які потім можна розфарбувати самостійно. У цих регіонах є лише регіони N^1 і N^2 (N = N^1 + N^2), тепер їм потрібно не більше 4^N1 + 4^N2 спроб, що набагато менше, ніж 4^N1 * 4^ N2 = 4^N спроб.

Якщо ми хочемо знайти найменшу кількість кольорів, які можуть забарвити дану карту, то спочатку потрібно перевірити, чи достатньо 2 кольорів. Це можна зробити ефективно.

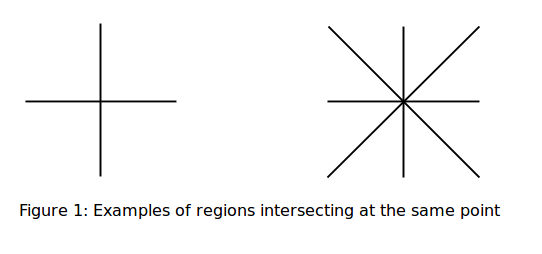
Якщо потрібно використовувати лише два кольори A і B, а один з регіонів вже має колір, то обхід точки перетину фіксує колір усіх інших регіонів: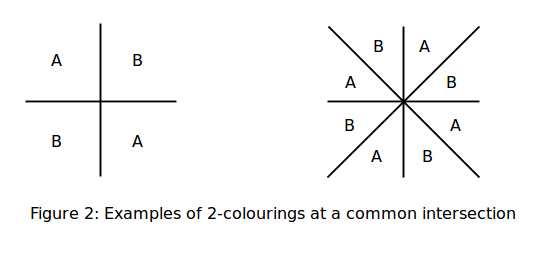

Це правило також корисне для першої спроби розфарбовування карт, які потребують 3 або 4 кольори. Наприклад, якщо регіон 1 нижче вже має колір А, то регіони 2 і 4 потребують іншого кольору, і ми не маємо уявлення, яким він може бути, але ми знаємо, що забарвлення кольором А регіону 3 не створює додаткових умов щодо забарвлення регіонів 2 і 4, оскільки вони вже мають сусіда кольору А.

Малюнок 3 показує лише невелику частину карти, але наведену вище евристику можна зробити більш точною для будь-якої карти. Якщо всі сусіди регіону 3 (на Малюнку 3 - регіони 2 і 4) мають принаймні одного сусіда кольору А (на Малюнку 3 - регіон 1), то забарвлення регіону 3 кольором А не може бути помилкою. Причина в тому, що забарвлення регіону 3 кольором A не створює жодних нових обмежень для сусідів, оскільки їм вже заборонено мати колір A. Отже, якщо в подальшому процесі фарбування виявиться, що ми припустилися помилки (через недостатню кількість кольорів), то немає сенсу надавати регіону 3 інший колір, ніж А, необхідно спробувати по-іншому розфарбувати інші регіону.

Що робити, якщо регіон 3 вище також є діагональним сусідом з іншим регіоном, скажімо, регіоном 9, яка вже має інший колір, наприклад колір В? Область 3 слід зафарбувати кольором А чи В? Тут також допоможе перевірити всіх сусідів області 3, чи їм вже заборонено мати колір А чи заборонено мати колір В. Якщо таких заборон немає, ми можемо зачекати з розфарбуванням 3.