300000
English | Français | فارسی | 中文 | Українська | Azerbaijani | ខ្មែរ | Tiếng Việt | Bahasa Melayu | Deutsch | O'zbek | Русскийtosh to'ldirish©
G'alabalarning umumiy soni: 209822
Floodfill uchun qo'llanma
Xaritani ranglash uchun minimal sonli ranglardan foydalanish muammosi uzoq tarixga ega, masalan, bu Vikipediya maqolasida tushuntirilgan. 4 rang har doim tekislik xaritasini ranglash uchun etarli degan teoremas, inson ishlab chiqargan "matematik" isbot orqali emas, balki faqat kompyuter tomonidan isbotlanishi mumkin bo'lgan birinchi katta matematik teoremasi sifatida mashhur bo'ldi.
Har doim xaritalarni samarali ravishda ranglaydigan hech qanday algoritm ma'lum emas. "Samarali" bilan biz shuni nazarda tutamizki, agar N mintaqalari soni juda katta bo'lsa, unda kerakli bo'yash urinishlari soni faqat Nk kabi o'sadi, bu erda k - N ga bog'liq bo'lmagan son. Boshqacha qilib aytganda, "samarali" algoritmlar uchun urinishlar soni faqat N polinomi kabi o'sadi. Buning o'rniga, ma'lum bo'yash algoritmlari eksponentsional murakkablikka ega, ya'ni urinishlar soni 4N kabi N ga bog'liq.
Agar 5 yoki 6 rangdan foydalanishga ruxsat berilgan bo'lsa yoki xaritaga faqat 2 rang kerak bo'lsa, samarali algoritmlar ma'lum.
Samarali usulni olishning yana bir imkoniyati algoritmning HAR DOIM samarali bo'lishi talabini bekor qilishdir. Hech bo'lmaganda ko'p hollarda ishlaydigan bunday evristik (ya'ni ko'rsatmalar to'plami) quyida muhokama qilinadi:
Q. Qaysi mintaqa birinchi bo'lib ranglanishi kerak?
- Avvaliga iloji boricha ko'proq qo'shnilari bo'lgan mintaqani bo'yash foydalidir, chunki agar bu mintaqa A rangini olsa, uning barcha qo'shnilari A rangini olmaslik uchun cheklovga ega bo'ladilar. Bu qo'shni mintaqalar uchun rang tanlovlari sonini kamaytiradi va shu bilan bo'yash qiyin bo'lsa, keyingi urinishlar sonini kamaytiradi.
Q. Qaysi ranglarni tanlash bepul?
- Birinchi bo'yashda ishlatiladigan rang, albatta, bepul.
- Bir mintaqani bo'yash uchun birinchi marta ikkinchi rang ishlatilganda, agar bu mintaqa birinchi rangli mintaqaga tegsa, ya'ni ikkinchi rang kerak bo'lsa, bu rang tanlovi erkindir.
- Mintaqani bo'yash uchun birinchi marta uchinchi rang ishlatilganda, agar bu mintaqa birinchi rangli mintaqaga va ikkinchi rangli mintaqaga tegsa, ya'ni uchinchi rang kerak bo'lsa, bu rang tanlovi erkindir.
Q. Keyingi qaysi mintaqa ranglanishi kerak?
- Biz bu rangda xato qilmasligimiz uchun faqat bitta mumkin bo'lgan rang qolgan mintaqani ranglashimiz kerak.
- Bo'yash urinishlari soni aniq 4 N dan kam (barcha N mintaqalari uchun barcha 4 ranglarni sinab ko'rish). Shunday qilib, bo'yash urinishlarining bu soni N mintaqalari soniga bog'liq. Binobarin, agar bo'yash xaritaning oq (rangsiz) qismini alohida, uzilgan oq kichik xaritalarga ajratsa, ular o'z-o'zidan ranglanishi mumkin. Bu hududlarda faqat N1 va N2 mintaqalari bor (N = N1 + N2), hozir eng ko'pi bilan faqat 4N1 + 4N2 urinib ko'rishadi, bu 4N1 × 4N2 = 4N urinib ko'rishadi.
- Agar berilgan xaritani ranglashi mumkin bo'lgan eng kichik ranglarni topishni istasa, avval 2 rang etarliligini tekshirish kerak. Bu samarali amalga oshirilishi mumkin.
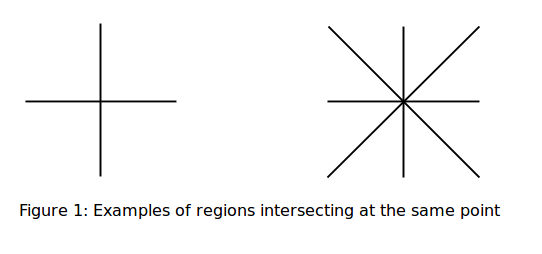
Agar faqat ikkita rang A va B ishlatilishi kerak bo'lsa va mintaqalardan biri allaqachon rangga ega bo'lsa, unda kesishma nuqtasini aylanib o'tish boshqa barcha mintaqalarning rangini tuzatadi: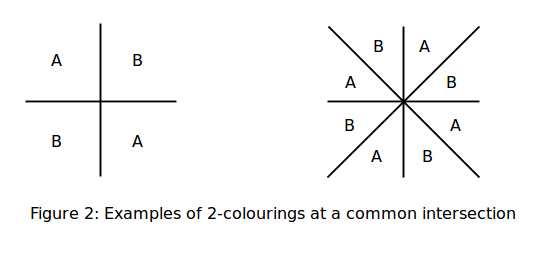
Bu qoida 3 yoki 4 rangga muhtoj bo'lgan xaritalarning birinchi rangini bo'yash urinishi uchun ham foydalidir. Misol uchun, agar quyidagi 1-mintaqa allaqachon A rangiga ega bo'lsa, unda 2 va 4 mintaqalari boshqa rangga muhtoj va biz bu nima bo'lishi mumkinligini bilmaymiz, lekin biz bilamizki, 3 mintaqasini A rangi bilan bo'yash 2 va 4 mintaqalarining rangiga qo'shimcha shartlar qo'ymaydi, chunki ular allaqachon A rangining qo'shnisiga ega.
Shakl 3 xaritaning faqat kichik qismini ko'rsatadi, lekin yuqoridagi evristik mumkin har qanday xarita uchun aniqroq bo'lishi kerak. Agar 3-mintaqaning barcha qo'shnilari (3-rasmda, 2 va 4-mintaqalar) A rangining kamida bitta qo'shnisiga ega bo'lsa (3-rasmda, 1-mintaqa), unda 3-mintaqani A rangi bilan bo'yash xato bo'lishi mumkin emas. Buning sababi shundaki, 3-mintaqani A bilan bo'yash qo'shnilariga hech qanday yangi cheklov qo'ymaydi, chunki ular allaqachon A rangiga ega bo'lish taqiqlangan. Shunday qilib, agar keyingi bo'yash jarayonida xato qilinganligi aniqlansa (chunki ranglar soni etarli emas), unda 3-mintaqaga A-dan boshqa rang berishning ma'nosi yo'q, boshqa ranglarni qayta sinab ko'rish kerak. - Agar yuqoridagi 3-mintaqa ham boshqa mintaqaga diagonal qo'shni bo'lsa, masalan, 9-mintaqa, B rangi kabi boshqa rangga ega? 3 A yoki B bilan ranglanishi kerakmi? Shuningdek, bu erda 3 ning barcha qo'shnilarini tekshirishga yordam beradi, ular allaqachon A rangiga ega bo'lish taqiqlanganmi yoki B rangiga ega bo'lish taqiqlanganmi. Agar ikkalasi ham bo'lmasa, biz 3 bilan bo'yash bilan kutishimiz mumkin.
Follow or subscribe for updates: