Bãi rác©
Tổng số trận thắng: 209822
Hướng dẫn chơi trò Floodfill
Việc sử dụng số lượng màu sắc ít nhất có thể để tô màu bản đồ có lịch sử lâu đời như đã giải thích, ví dụ như trong bài viết trên Wikipedia https://en.wikipedia.org/wiki/Four_color_theorem. Định lý rằng 4 màu luôn là đủ để tô màu một bản đồ mặt phẳng đã trở nên nổi tiếng như một định lý toán học lớn đầu tiên chỉ có thể được chứng minh bằng máy tính mà không phải thông qua một bằng chứng 'toán học' do con người tạo ra.
Không có thuật toán nào được biết là sẽ luôn tô màu bản đồ một cách hiệu quả. 'Hiệu quả' ở đây có nghĩa là nếu số vùng N rất lớn thì số lần tô màu cần thiết chỉ tăng lên giống như Nk trong đó k là số không phụ thuộc vào N. Nói cách khác, đối với các thuật toán 'hiệu quả', số lần thử chỉ tăng lên giống như một đa thức của N. Thay vào đó, các thuật toán tô màu hiện có cái gọi là độ phức tạp theo cấp số nhân, tức là số lần thử phụ thuộc vào N như 4N.
Nếu một người được phép sử dụng 5 hoặc 6 màu, hoặc nếu bản đồ chỉ cần 2 màu, thì các thuật toán hiệu quả được công nhận.
Một cơ hội khác để có được một phương pháp hiệu quả là loại bỏ yêu cầu rằng thuật toán LUÔN LUÔN hiệu quả. Phương pháp heuristic như vậy (tức là một tổ hợp các hướng dẫn) ít nhất có hoạt động trong các trường hợp sẽ được thảo luận dưới đây:
- Việc ưu tiên tô màu cho một vùng có nhiều vùng lân cận nhất sẽ rất có ích vì nếu vùng đó có màu A thì tất cả các vùng lân cận của nó sẽ không được dùng màu A. Điều này làm giảm số lựa chọn về màu sắc cho các vùng lân cận này và do đó giảm số lần thử sau này nếu việc tô màu trở nên khó khăn.
- Trong lượt tô màu đầu tiên, ta chắc chắn sẽ được thoải mái lựa chọn.
- Lần đầu tiên mà màu thứ hai được sử dụng, có thể tự do lựa chọn màu sắc này nếu vùng được tô tiếp xúc với một vùng sử dụng màu đầu tiên, có nghĩa việc dùng một màu thứ hai là cần thiết.
- Lần đầu tiên mà màu thứ ba được sử dụng, có thể tự do lựa chọn màu sắc này nếu vùng được tô tiếp xúc với một vùng sử dụng màu đầu tiên và một vùng sử dụng màu thứ hai, có nghĩa một màu thứ ba là cần thiết.
- Chúng ta nên tô màu cho một vùng tiếp theo khi vùng này chỉ có thể tô một màu duy nhất khả thi để chúng ta không mắc lỗi khi tô màu này.
- Số lần thử tô màu luôn ít hơn 4N (thử cả 4 màu cho tất cả N vùng). Vì vậy, số lần thử tô màu này phụ thuộc rất nhiều vào số vùng N. Do đó, sẽ rất hữu ích nếu việc tô màu chia phần màu trắng (chưa tô màu) của bản đồ thành các bản đồ con màu trắng riêng biệt không kết nối với nhau mà sau đó lại tiếp tục được tô màu theo cách riêng. Những vùng này chỉ có N1 và N2 vùng (N = N1 + N2), bây giờ chỉ cần nhiều nhất là 4N1 + 4N2 lần thử mà rõ ràng là nhỏ hơn nhiều so với 4N1 × 4N2 = 4N lần thử.
- Nếu một người muốn tìm số lượng màu tối thiểu để có thể tô màu cho một bản đồ nhất định thì trước tiên người ta phải kiểm tra xem liệu 2 màu có đủ không. Điều này có thể được thực hiện một cách hiệu quả.
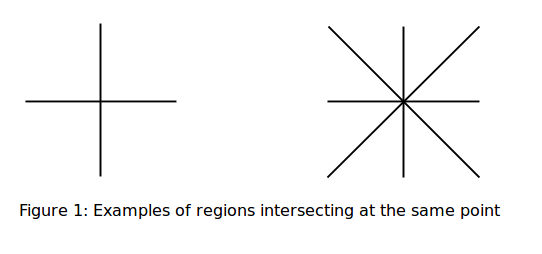
Nếu chỉ sử dụng hai màu A và B và một trong số các vùng đã có màu, thì việc di chuyển xung quanh điểm giao nhau sẽ sửa màu của tất cả các vùng khác: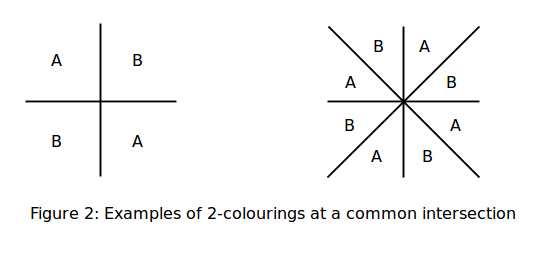
Quy tắc này cũng hữu ích để áp dụng cho lần thử tô màu đầu tiên của bản đồ cần 3 hoặc 4 màu. Ví dụ: nếu vùng 1 bên dưới đã có màu A thì vùng 2 và 4 cần một màu khác và ta không biết đó có thể là màu gì nhưng ta biết rằng việc tô màu vùng 3 với màu A không làm nảy sinh thêm các điều kiện về tô màu của vùng 2 và 4, bởi vì chúng sẵn đã tiếp xúc một vùng lân cận có màu A.
Hình 3 chỉ thể hiện một phần nhỏ của bản đồ tuy nhiên phương pháp heuristic ở trên có thể được thực hiện một cách chính xác đối với bất kỳ bản đồ nào. Nếu tất cả các vùng lân cận của vùng 3 (trong Hình 3, vùng 2 và 4) có ít nhất một vùng lân cận sử dụng màu A (trong Hình 3, vùng 1), thì việc tô màu vùng 3 với màu A sẽ không gây ra lỗi sai nào. Lý do là việc tô màu vùng 3 với màu A không tạo ra bất kỳ hạn chế nào đối với các vùng xung quanh nó bởi vì chúng vốn đã không được sử dụng màu A. Vì vậy, nếu trong quá trình tô màu tiếp theo, cuối cùng lại xảy ra một lỗi sai (vì số lượng màu không đủ), thì việc cho khu vực 3 một màu khác với màu A là vô nghĩa, một số màu khác phải được thay đổi. - Điều gì sẽ xảy ra nếu vùng 3 ở trên cũng là vùng tiếp xúc theo đường chéo của vùng khác, chẳng hạn như vùng 9 đã có một màu khác ví dụ là màu B? Câu hỏi là vùng 3 nên được tô màu A hay B? Ở trường hợp này nó cũng giúp kiểm tra tất cả những vùng xung quanh của 3 xem chúng có bị hạn chế không được tô màu A hay không được tô màu B không. Nếu đều không hạn chế tô màu nào cả thì chúng ta có thể tạm thời chưa vội tô vùng 3.






Theo dõi cập nhật sắp tới