填充©
这个谜题赢了/玩了: 16205/24689

 我为什么要阅读这个《深思熟虑》?
我为什么要阅读这个《深思熟虑》?
因为你会感到惊讶。
 在尝试了一些装箱谜题之后,您认为哪个数学领域对解决它们最有用:
在尝试了一些装箱谜题之后,您认为哪个数学领域对解决它们最有用:
1) 代数,2) 概率论,3) 几何,4) 数论,5) 对称性,6) 另一个领域?
事实证明,最有用的是考虑数字的可整除性,尤其是被 2 整除的可整除性。这是数论的一个主题。我们堆叠的东西是几何对象,但这并不意味着需要几何知识来解决难题。从 Geometry 中,我们需要知道正方形或矩形的面积是多少,但仅此而已。
对于一些谜题,考虑对称性也非常有用。
 快速提示
快速提示
这些是给那些寻求帮助但对数学背景不感兴趣的人的提示。
- 通过查看每个谜题的 “This puzzle won/played” 旁边的数字,检查哪些是最简单的。从最简单的谜题开始总是一个好主意,它会让你练习处理界面。
- 谜题“2×3×3 1”和“2×3×3 2”很容易通过反复试验来解决。
- 如果您第一次尝试 “1×7×10 1” 谜题没有成功,请在下次尝试时轮换棋子。
- “1×7×7 1”是一个思考对称性会有所帮助的谜题。原因是容器(网格)有一个方形的底座,有 4 个等长的边,我们有 4 个相同形状的长块。因此,应该将它们对称地放入。只有一个紫色的方形块。要获得 90° 旋转对称的解决方案,这块必须位于中间。任何其他地方都会打破溶液的 90° 对称性。
- 按钮较暗的谜题需要更多的思考。首先要完全理解 “3×3×3 2” 谜题,然后再进入 5×5×5 谜题。
 如何在不试错的情况下解决这些难题呢?
如何在不试错的情况下解决这些难题呢?
以下是一些提示:
- 将一个难题拆分为更简单的问题,即拆分为子目标。例如,要填充整个容器,需要填充每一层。
- 以对称的方式排列各个部分,特别是如果容器是对称的,例如 3×3×3 立方体或 1×7×7 方形容器。
- 充分利用给定的信息。这些作品的尺寸是多少?他们中有多少是相同的形状?
这个“深思熟虑”的其余部分的目标是在不试错的情况下解决所有谜题,而是提出简单的问题并回答它们。
 定义
定义
为清楚起见,以下是我们将用于讨论装箱问题的一些术语:
 积木块
积木块
将组合在一起以形成较大实体的形状之一。
奇数是长度均为奇数的积木块,例如 1×1×1 或 1×3×5。
一个积木块即使至少有两个偶数长度,例如 1×2×4 或 2×2×2。
 所有积木块都是偶数还是奇数?
所有积木块都是偶数还是奇数?
不。一个长度正好为偶数的积木块,例如 1×2×3,不符合任何一个定义。在以下部分中,我们将重点介绍奇数和偶数。
 长方体/容器
长方体/容器
长方体是一个矩形棱柱体。我们使用 “container” 一词来指代 cuboid 的空 shell。我们将 “cuboid” 称为容器的内容。容器将装满碎片,并从碎片创建长方体。
 层
层
层是沿平行于容器面的方向的厚度为 1 的切片。一个 3×4×5 的容器有 3 层 4×5,4 层 3×5 和 5 层 3×4。
 一个 1×5×7 的容器有多少层?
一个 1×5×7 的容器有多少层?
它有 1 个 5×7 层、5 个 1×7 层和 7 个 1×5 层。它总共有 1 + 5 + 7 = 13 层。
 立方体
立方体
具体来说,是一个 1×1×1 的立方体,而不是一个更大的立方体。一个 1×1×1 的棋子由 1 个立方体组成,而一个 1×1×3 的棋子由 1 × 1 × 3 = 3 个立方体组成。
 积木
积木
几个相互连接的块形成一个 Building Block。有趣的构建块将具有对称性。对于更难的谜题,几个相同或镜像相同的构建块加上一个中心块将填满容器。
 策略
策略
解决难题的一半是将难题拆分成更小的问题。
要做到这一点,一个人应该问自己一些简单的问题。以下问题将有助于解决包装难题。
 每个长方体都可以用 1×2×2 的积木块形成吗?例如,可以只用 1×2×2 的积木块形成 3×3×3 的长方体吗?
每个长方体都可以用 1×2×2 的积木块形成吗?例如,可以只用 1×2×2 的积木块形成 3×3×3 的长方体吗?
不。一个 1×2×2 的积木块由偶数个立方体组成。因此,任意数量的 1×2×2 积木块加起来将有偶数的立方体总数。由于 3×3×3 长方体由奇数个立方体组成,因此不能以这种方式形成。
在接下来的几节中,我们将探讨可整除性(尤其是 2)如何决定必须如何放置积木块来解决某些谜题。
 1×2×2 可以至少填满 3×3×3 容器的任何一层吗?
1×2×2 可以至少填满 3×3×3 容器的任何一层吗?
答案又是否定的。图层中可以被一个积木块占据的面积是该积木块的一个面的面积,对吧?
 1×2×2 的积木有哪些面?
1×2×2 的积木有哪些面?
一个 1×2×2 的积木块有两对平行的 1×2 面,还有一对 2×2 的面。
 这些面的区域是什么,这些区域有什么共同点?
这些面的区域是什么,这些区域有什么共同点?
面积是 1 × 2 = 2 和 2 × 2 = 4。2 和 4 都是偶数。
我们观察到一个 1×2×2 的积木块在每层只能占据偶数个立方体(2 或 4)。
 所有偶数积木块都是如此吗?
所有偶数积木块都是如此吗?
积木块的每个面都有两个长度。由于偶数积木块最多只有一个奇数长度,因此它们的每个面都将至少有一个偶数长度。因为 even × odd = even,所以每个面的面积将是 even。这就是为什么我们称它们为偶数积木块!
我们了解到,奇数边长的长方体不能仅由偶数块形成。具有奇数区域的图层也不能用偶数块填充。因此,题干“3×3×3 2”有几个 1×1×1 的积木块,都是奇数积木块。
以下是另一个需要考虑的有用问题:
 两种类型的积木块(1×1×1 和 1×2×2)中的一种是否比另一种更“珍贵”?
两种类型的积木块(1×1×1 和 1×2×2)中的一种是否比另一种更“珍贵”?
是的。如果我们只有 1×1×1 的积木块,那么任何题干都是微不足道的,你同意吗?如果我们只有 1×2×2 的积木块,那么一个奇数的箱子就无法装满,如上所示。
显而易见的问题是: 可以装满 3×3×3 容器的 1×1×1 的最小数量是多少?
自然会出现以下问题:
 为什么三个 1×1×1 就足够了?
为什么三个 1×1×1 就足够了?
为了回答这个问题,我们将奇数层(奇数面积的层数)与可以填充偶数块且只能填充 3 个立方体的奇数层数进行比较。
 一个 3×3×3 的容器有多少层?
一个 3×3×3 的容器有多少层?
在三个方向(宽度、高度、深度)中,容器都有 3 层。当容器装满时,会填充 3 + 3 + 3 = 9 个奇数层。
 一个 1×1×1 可以完成多少个奇数 3×3 的积木块(还有一些偶数的 1×2×2)呢?
一个 1×1×1 可以完成多少个奇数 3×3 的积木块(还有一些偶数的 1×2×2)呢?
三层:水平层和两个垂直层,其中包含 1×1×1 块。因此,3 个立方体最多可以填充 3 × 3 = 9 层。
这表明 3 个立方体是必要的,而且因为“3×3×2 2”的谜题是可以解决的,所以 3 个立方体也足以填满 9 个奇数层。
 这告诉我们 3 个立方体在
“3×3×3 2” 拼图?
这告诉我们 3 个立方体在
“3×3×3 2” 拼图?
在 9 层中的每一层中,只能有 1 个立方体,不能有 0 个立方体,也不能有 2 个立方体!否则,3 个立方体将不足以容纳 9 个图层。
这是解决方案的突破。此外,放置立方体的唯一方法是沿对角线放置 - 一个立方体在中心,另外两个立方体在对角线对角。否则,笨重的 1×2×2 块将太大,无法填满 3 个立方体周围的空间。
因此,将一个立方体放在一个角落里,然后以对称的方式围绕该立方体放置三个 1×2×2 的块。将一个立方体放在中心,一个放在对面的角落,其余的就会很明显。
 我们还能从这个解决方案中学到什么?例如,它有对称性吗?
我们还能从这个解决方案中学到什么?例如,它有对称性吗?
将第一个立方体放在角落里,并在其周围放置三个 1×2×2 块后,对称性就可见了。该解决方案具有 120° 旋转对称性,立方体的对角线作为旋转轴(120° = 完整圆旋转的 1/3)。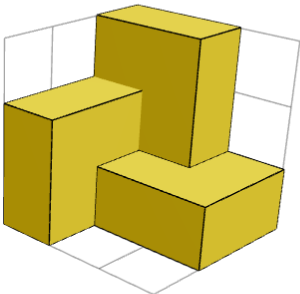
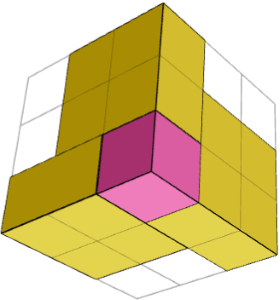
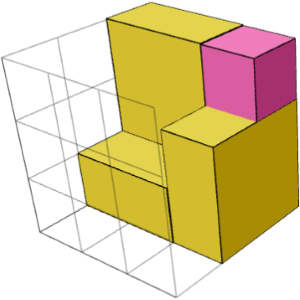
 解决方案是相同还是对称的构建块的总和,每个构建块由几个部分组成?
解决方案是相同还是对称的构建块的总和,每个构建块由几个部分组成?
是的。长方体是 2 个镜像对称的构建块(角落中的 1 个立方体 + 周围的 3 个 1×2×2 块)和中间的 1 个立方体的总和。上面的 2 张图片显示了 2 个侧面的一个构建基块。
 有没有其他方法可以使用不同的构建块来解决这个难题?
有没有其他方法可以使用不同的构建块来解决这个难题?
是的。下面的左图和右图显示了 “3×3×3 2” 谜题的两个镜像对称构建块。它们可以与中心立方体(中间图像)组合来解决难题。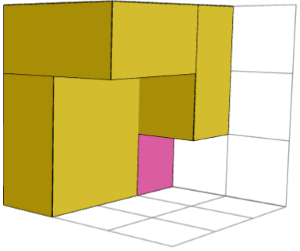
 我们为什么要费心考虑构建块呢?
我们为什么要费心考虑构建块呢?
使用少量给定的碎片并从中创造对称的东西比用所有碎片填充较大的容器更容易。
 积木可以用来解决更大的谜题吗,比如 “3×5×7 1” ?
积木可以用来解决更大的谜题吗,比如 “3×5×7 1” ?
是的。较大的容器,即使它们的长度都不同,也可以使用相同/镜像对称的构建块进行填充。有多种方法可以解决 “3×5×7 1” 的谜题,使用积木和中心奇数。我们留给您找一些例子。
 我们如何知道哪些部分应该构成构建块?
我们如何知道哪些部分应该构成构建块?
让我们先考虑一个奇数长方体的中心。因为中心位置是唯一的,所以如果我们想要一个对称的解,中心必须被一个与容器形状相同的块占据。3×3×3 长方体是一个立方体,因此其中心部分需要是一个立方体。中间的 1×2×2 会打破对称性。
这意味着我们有 6 个黄色和 3 个 − 1 = 2 个粉红色的积木来构建许多相同的构建块。
 我们应该尝试创建多少个构建块?
我们应该尝试创建多少个构建块?
构建块应形成长方体减去中心部分。因此,构建块中的黄色块数必须是 6(黄色块的总数)的除数,构建块的粉红色块数需要除以 2(为中心保留 1 后剩余的粉红色立方体数)。
因此,相同构建块的数量 N 是相同块数量的最大公约数,这里是 6 和 2,即 GCD(6,2) = 2。因此,我们应该从 2 / 2 = 1 个粉红色立方体和 6 / 2 = 3 个黄色块中创建一个构建块。这就是我们所做的。
 总结数学算法以将其用于更大的谜题。
总结数学算法以将其用于更大的谜题。
对于奇数容器:
- 对齐奇数块以确保它们在任何图层中都不会重叠。它们应该将容器的一个角与容器的另一角连接起来。如果奇数块是立方体,则它们形成对角线。如果奇数较大 (1x1x3),则它们形成非直对角线。
- 如果只有一种类型的偶数棋子,则使用它们来填充容器。
- 如果有不同类型的偶数棋子:
- 把中间的奇数放在一边。从剩余的棋子中,找到不同类型棋子数量的最大公约数 N。N 是构建块的数量。
- 创建 N 个相同的构建块,并将它们与中心块放在一起,以防出现奇怪的容器。
虽然小谜题可以通过反复试验轻松解决,但这种策略不适用于较大的谜题。我们对奇数和偶数棋子的探索揭示了一个重要原因:奇数棋子的放置至关重要,因为正确放置它们的方法很少。使用反复试验,人们可以在一开始就犯错误,只有在放置许多作品后才意识到出了问题。这使得确定导致错误的原因变得非常困难,因此没有可用的反馈;试错法对较大的容器无效。需要思考。
 只用一种类型的件进行包装
只用一种类型的件进行包装
在本节中,我们将探讨可以由单一类型的块形成的长方体的大小。这是一个理论部分,不是解决上述谜题所必需的。本节不需要困难的数学运算。
有了足够的 1×1×1 块,我们可以轻松形成任何大小的长方体。但是其他棋子呢,比如 2×3×4 或 1×2×5 棋子呢?有两个主要问题需要研究。首先, 给定一个块的长度和一个长方体的长度,我们如何确定是否可以从该块的副本创建长方体? 其次, 我们如何从一个单独的部分开始,生成可以形成的长方体的长度? 在本节中,我们将在探讨这两个重要问题的同时考虑更简单的问题。
 一个 2×6×10 的长方体可以只由 1×2×5 组成吗?
一个 2×6×10 的长方体可以只由 1×2×5 组成吗?
是的!三个 1×2×5 可以并排放置,形成 1×6×5 的形状 (3 × 2 = 6)。然后,我们可以创建第二个 1×6×5 形状,并将它们组合成一个 1×6×10 形状。最后,可以将两个 1×6×10 的形状放在一起,形成一个 2×6×10 的长方体。
 是否可以仅使用 2×5×6 的块形成 10×12×14 长方体?
是否可以仅使用 2×5×6 的块形成 10×12×14 长方体?
 提示
提示
没有必要想象这些作品将如何排列。
 另一个提示?
另一个提示?
2×5×6 的棋子与 5×6×2 的棋子相同,因为它可以旋转。
 答
答
是的。由于 10 / 5 = 2,12 / 6 = 2,14 / 2 = 7,因此较大的长方体可以被认为是 5×6×2 的 2×2×7 排列。5×6×2 块都可以以相同的方向放置。
 我们如何推广这些发现?
我们如何推广这些发现?
假设我们只有大小为 x × y × z 的块。如果存在正整数 A、B、C,使得 Ax、By 和 Cz 按某种顺序等于 X、Y 和 Z,则可以构造 X × Y × Z 长方体。
 在这种情况下将使用多少块?
在这种情况下将使用多少块?
我们可以将 A 块放在一个方向上, B 放在另一个方向上, C 放在第三个方向上。总共将使用 A > times B × C 棋子。
 为什么 Ax、 By 和 Cz 可以任意顺序等于 X、 Y 和 Z ?
为什么 Ax、 By 和 Cz 可以任意顺序等于 X、 Y 和 Z ?
大小为 X × Y × Z 的容器与 Z × X × Y 长方体相同。长度的顺序无关紧要,因为长方体可以旋转。
 对于一些正整数 A、B、C,任何由 1×2×3 组成的长方体都必须具有长度 A、B 和乘以 2、C 和乘以 3,这是真的吗?
对于一些正整数 A、B、C,任何由 1×2×3 组成的长方体都必须具有长度 A、B 和乘以 2、C 和乘以 3,这是真的吗?
不。如果所有 1×2×3 的棋子都朝向同一方向,则长方体的大小为 A × (B × 2) × (C × 3)。但是块的方向可以不同,并且仍然形成一个长方体。例如,1×2×3 可以形成一个 1×5×6 的长方体,即使 1、5 和 6 不等于 A、 B 和times 2,以及 C × 3 在任何顺序上。再比如拼图“1×7×10 1”,它由 1×2×5 组成。
 在这两个例子中,棋子的长度和长方体的长度之间有什么关系?
在这两个例子中,棋子的长度和长方体的长度之间有什么关系?
在这两个例子中,长方体的一个长度是该块的两个长度之和。长方体的不同长度是相同两个长度的 LCM(最小公倍数)。在由 1×5×6 块形成 1×2×3 长方体的情况下,我们有 1×5×6 = 1 × (2 + 3) × LCM(2,3)。同样,1×7×10 = 1 × (2 + 5) × LCM(2,5)。
 我们如何利用这一事实来找到一种方法来生成可以从给定部分构建的长方体的长度?
我们如何利用这一事实来找到一种方法来生成可以从给定部分构建的长方体的长度?
我们首先将一个片段的长度表示为有序的三元组。例如,一个 1×2×3 的棋子用 (1, 2, 3) 表示。现在,我们可以重复执行 3 个操作来给出可以从这块形成的长方体的长度。他们是:
- 更改长度的顺序。这称为 排列。在我们的例子中,它表示 3D 空间中的旋转。一个例子是
(1, 2, 3) → (2, 3, 1)。 - 将长度分别乘以正整数 A、B 和 C。这相当于通过将 A 块放在一个方向上,B 放在另一个方向上,C 沿第三个方向放置来形成一个更大的长方体。例如,我们可以将 1、4 和 3 相乘,得到 (1, 2, 3) → (1 × 1, 4 × 2, 3 × 3) = (1, 8, 9)。
- 取两个长度,一个用他们的总和替换,一个用他们的 LCM 替换..这相当于形成一个更大的长方体,其中的块朝向不同方向。例如,选择长度 2 和 3,我们将得到 (1, 2, 3) → (1, 2 + 3, LCM(2,3)) = (1, 5, 6)。
 可以以第 4 种 方式组合这些块以产生形状与第 3 次 操作结果不同的长方体吗?
可以以第 4 种 方式组合这些块以产生形状与第 3 次 操作结果不同的长方体吗?
是的。考虑一个大小为 x × y × z 的片段。第三次操作生成大小为 x × (y + z) × LCM(y,z) 的长方体,其中从块到长方体的一个长度 x 保持不变。
一种类似但不同的方法是像以前一样,将 LCM(y,z)/y 许多块再次并排放置,LCM(y,z)/y 许多块彼此相邻,但现在将一组旋转 90°,使两个块具有相同的长度 LCM(y,z),但高度不同。在数学术语中,我们没有将 x × y × LCM(y,z) 和 x × z × LCM(y,z) 附加到 x × (y + z) × LCM(y,z) 中。相反,其中一个,比如 x × z × LCM(y,z),被旋转到 z × x × LCM(y,z),然后附加。
然后,矩形底面积不是 (y + z) & 乘以 LCM(y,z),而是 (x + z) & 乘以 LCM(y,z)。然后,两个构建块 x × y × LCM(y,z) 和 z × x × LCM(y,z) 在 X 方向上的长度分别为 x 和 z。
堆叠 LCM(x,z)/x 多个高度为 x 和 LCM(x,z)/z 的构建块,两个堆叠都达到高度 LCM(x,z)。当它们被连接时,结果是一个大小为 LCM(x,z) × (x + z) × LCM(y,z) 的长方体,其形状和大小与第三次操作产生的任何长方体不同。
可以按任何顺序重复这些操作,首先从一个块生成一个长方体,然后将该长方体用作“块”来生成更大的长方体。我们之前讨论了如何从 1×2×5 形成 2×6×10 的长方体。在这种情况下,只需要一个运算,分别乘以 2、3 和 2:(1, 2, 5) → (2 × 1, 3 × 2, 2 × 5) = (2, 5, 10)。
因此,大小为 x × y × z 的块不仅可以构造大小为 Ax × By × Cz 的长方体,而且,例如,还可以构造大小为 x × (y + z) × LCM(y,z) 的长方体,其中 LCM(y,z) 是 y 和 z 的最小公倍数。将其中几个构建块放在一起,得到大小为 Ax &x 乘以 B(y + z) + C(LCM(y,z)) 的长方体。
我们现在将研究一种特殊类型的棋子。如果一个乐曲的每个较大长度都可以被下一个较小的长度整除,则该乐曲是 泛音 。例如,一个 1×2×6 的棋子是泛音,因为 2 / 1 = 1 和 6 / 2 = 3。1&乘以 4&乘以 6 的棋子不是谐波,因为 6 不是 4 的倍数。
 是 1×2×3 的谐波吗?
是 1×2×3 的谐波吗?
否,因为 3 不能被 2 整除。
 是什么让 harmonic pieces 在包装中特别?它们与我们关于块和长方体长度的讨论有什么关系?
是什么让 harmonic pieces 在包装中特别?它们与我们关于块和长方体长度的讨论有什么关系?
我们已经观察到,任何块都可以形成一个长方体,其长度是块长度的倍数。事实证明,由相同谐波块形成的任何长方体的长度 必须是 块长度的倍数。也就是说,如果一个谐波块的长度为 x、 y 和 z,则由该块的副本形成的任何长方体都必须具有一个长度可被 x 整除,另一个长度可被 y 整除,第三个长度可被 z 整除。虽然这是一个简单的陈述,但证明需要的概念超出了本网站的范围。证明的链接可以在 “致谢” 部分找到。
 这个事实与我们上面讨论的四个操作如何一致?
这个事实与我们上面讨论的四个操作如何一致?
我们可以先把一个 piece 也看作是由 piece 的一个副本形成的长方体。 一个 x × y × z 块也是一个 x × y × z 长方体。这个长方体的长度是该块长度的倍数,因为每个数字都是自身的倍数。我们将展示为什么我们介绍的四种方法生成的长方体的长度仍然是工件长度的倍数。
- 更改长度的顺序 (排列):这只是一个旋转,实际上并没有改变长方体的长度。长方体的长度仍然是该块长度的倍数。
- 将长方体的长度乘以正整数:如果长方体的长度已经是该块长度的倍数,则不会改变。它们只会变成更大的倍数。如果 X = Ax 是 x 的倍数,则对于任何正整数 D,DX = DAx 也是 x 的倍数。
- 用它们的总和 和 LCM 代替两个长度:这就是为什么谐波件很重要的原因;我们需要使用和声作品的定义。假设我们从一个谐波块 (x, y, z) 开始,我们已经从中形成了长方体 (Ax, By, Cz)。长度的顺序无关紧要,因为长方体可以旋转。现在,我们将对长方体的任意两个长度执行第三个操作,比如 Ax 和 By:(Ax, By, Cz) → (Ax + By, LCM(Ax,By), Cz)。现在,由于棋子 (x, y, z) 是泛音的,因此两个长度 x 和 y 中的一个是另一个长度的倍数。假设 y 是 x 的倍数。因此,By 也是 x 的倍数,并且由于 Ax 也是,因此 Ax + By 之和是 x 的倍数。接下来,LCM(Ax,By) 是 Ax 和 By 的最小公倍数,因此根据定义它是 By 的倍数,因此它可以被 y 整除。最后,Cz 当然是 z 的倍数。因此,新长方体的长度 (Ax + By, LCM(Ax,By), Cz) 仍然是该块长度的倍数。
- 第四次手术呢? 由于此操作类似于第三个操作,因此上面给出的参数可以适用于这种情况。我们把它留作一种练习。
我们已经证明,在任何和声作品上以任何顺序重复执行这四个操作,将产生一个长方体的长度是该作品长度的倍数。需要注意的是,在我们讨论第三次操作(和第四次)时,我们依赖于这个乐曲是和声的事实。当一个 piece 不是 harmonic 时,参数就失败了。这是 harmonic 和 non-harmonic 作品之间的主要区别。对于泛音,与前两种方法相比,第三种和第四种方法不会产生额外的形状。
因此,由谐波块形成的任何长方体都可以具有相同方向的所有块。因此,如果我们试图用相同的谐波块形成一个长方体,那么尝试将它们都面向同一方向就足够了。如果这是不可能的,那么根本无法形成长方体。
由于一个 1×2×2 的块是谐波的,所以由这个块的副本形成的任何长方体都必须具有长度 A、B 和时间 2,对于一些整数 A、B 和 C,长度必须为 C 和时间 2。下图显示了一个 5×4×4 长方体,由 1×2×2 块组成,它们都具有相同的方向。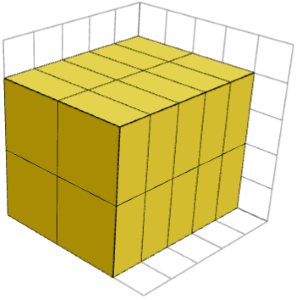
 A、B 和 C 的值是什么?
A、B 和 C 的值是什么?
设置 A、 B 和乘以 2,C 和乘以 2 分别等于 5、4 和 4,我们发现 A = 5 / 1 = 1,B = 4 / 2 = 2,C = 4 / 2 = 2。
 当用谐波片包装时,这些片必须朝向同一方向吗?
当用谐波片包装时,这些片必须朝向同一方向吗?
不!虽然所有棋子总是有可能具有相同的方向,但可能会有其他排列,但它们不会形成新的形状。下图显示了从 1×2×2 块形成 5×4×4 长方体的不同方法。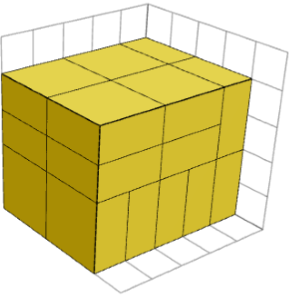
 非和声作品的规则是什么?
非和声作品的规则是什么?
当使用非谐波棋子 x × y × z 时,对于任何整数 A、B、C,可以形成一些大小不是 Ax × By × Cz 的长方体。例如,可以从 1×2×3 块创建 1×5×6 长方体。如前所述,这是第三个操作的结果。
需要注意的是,长方体中的立方体数量必须始终能被该块中的立方体数量整除。当立方体的长度不是棋子不同长度的倍数时,由于第三种和第四种方法,长方体的一个长度将是至少 2 个长度的公倍数。这一事实可用于确定某些长方体是否可以由非谐波块形成。
 回顾我们探索的内容:
回顾我们探索的内容:
 2&乘以4&乘以12块可以形成大小为4&乘以8&乘以36的长方体吗?大小为 10×10×12 的长方体呢?
2&乘以4&乘以12块可以形成大小为4&乘以8&乘以36的长方体吗?大小为 10×10×12 的长方体呢?
由于 4 / 2 = 2,8 / 4 = 2,36 / 12 = 3,因此可以形成 4×8×36 长方体。
10&乘以10×12 长方体的长度之一可以被 12 整除。其他长度是 10 和 10,两者都不能被 4 整除。因此,10&乘以10&乘以12长方体的长度不是该块长度的倍数。由于 12 / 4 = 3 和 4 / 2 = 2,该块是谐波的,因此 10×10×12 的长方体不能由尺寸为 2×4×12 的块形成。
 大小为 1×3×5 的块可以形成大小为 2×15×8 的长方体吗?3×9×14 长方体呢?
大小为 1×3×5 的块可以形成大小为 2×15×8 的长方体吗?3×9×14 长方体呢?
由于 5 不能被 3 整除,因此该棋子不是谐波。我们不能应用我们对和声作品的知识。
可以用这些块形成一个 2×15×8 的长方体。三个 1×3×5 可以形成 1×3×15(或 1×15×3)的形状,其中 5 个不同排列的棋子可以形成 1×15×5 的形状。这两个形状可以用来创建一个 1×15×8 的长方体,其中两个可以形成一个 2×15×8 的长方体。我们可以利用我们讨论的更简洁的操作:(1, 3, 5) → (1, 3 + 5, LCM(3,5)) = (1, 8, 15) → (2, 8, 15) → (2, 15, 8)。
每当 1×3×5 组合时,立方体的总数是 5 的倍数。由于 3 × 9 × 14 不能被 5 整除,因此不能用大小为 1×3×5 的块创建 3×9×14 的长方体。
 谐波和非谐波作品的规则总结
谐波和非谐波作品的规则总结
以下是我们所学到的知识概述:
- 如果长方体的长度是一块长度的倍数,那么它可以由该块的副本形成,而不管该块是否是泛音。这种长方体可以由所有块以相同的方向形成,但也可能存在块具有不同方向的排列。
- 如果一个 piece 是 harmonic,那么任何形成的 cuboid 的长度都必须是 piece 长度的倍数。因此,由谐波块形成的任何长方体都可以使所有块具有相同的方向,尽管这并不总是必要的。
- 如果一个乐曲不是和声的,则可以形成一些长方体,它们的长度不是乐曲长度的倍数(参见第三和第四个操作)。在这种情况下,棋子 不能 都具有相同的方向。使用非谐波块,可以使用前面描述的 4 种方法创建不同形状的长方体。
 这些观察结果仅在三维空间中有效吗?
这些观察结果仅在三维空间中有效吗?
不。在这种情况下,3 维并没有什么特别之处。事实上,将其中一个长度设置为等于 1 等效于将问题减少到 2 维。结果在超过 3 个维度中也有效。例如,1×3×12×24 是谐波。因此,对于某些正整数 A、B、C 和 D,由这些 4 维块形成的任何 4 维长方体都必须具有维度 A、B 和乘以 3、C 和乘以 12 以及 D 和乘以 24。
 如何获得动手拼图?
如何获得动手拼图?
我们无法告诉您如何制作 4 维作品 :)但是在 3-D 中,如果您有许多备用骰子,您可以将它们粘在一起形成碎片。
例如,人们可以使用鞋盒来代替 5×5×5 的盒子。如果一个人对角线握住它,这些棋子就会留在它们所在的位置。
一些谜题的高度为 1(例如,“1×7×10 1”),因此是 2 维谜题。人们可以从方格纸上剪下矩形作为这些拼图的碎片。
 确认
确认
我们在 数学展上看到木质版拼图“5x5x5 1”时,点燃了我们对打包拼图的兴趣。在引用其作者、著名数学家 约翰·霍顿·康威 (John Horton Conway) 之后,我们从他那里找到了谜题“3x3x3 2”、“5x5x5 2”和“5x5x5 3”。
“只用一种类型的工件包装”部分的灵感来自荷兰数学家 de Bruijn 的工作。要了解有关 de Bruijn 对包装矩形块的观察的更多信息,请参阅 这篇文章。你可以 在这里阅读 de Bruijn 对和声特性的证明。





关注或订阅更新: