Заливка©
Общее количество побед: 209822
Гайд по игре в Floodfill
Проблема использования минимального количества цветов для раскрашивания карты имеет долгую историю, как объясняется, например, в этой статье Википедии. Теорема о том, что 4 цвета всегда достаточны для раскрашивания карты плоскости, стала известна как первая большая математическая теорема, которая могла быть доказана только компьютером, а не с помощью «математического» доказательства, созданного человеком.
Не существует алгоритма, который всегда эффективно раскрашивал карты. Под "эффективно" мы подразумеваем, что если количество областей N очень велико, то количество необходимых попыток раскраски растет только как Nk, где k - число, которое не зависит от N. Другими словами, для «эффективных» алгоритмов количество попыток растет только как полином N. Вместо этого известные алгоритмы раскрашивания имеют так называемую экспоненциальную сложность, т.е. количество попыток зависит от N, как 4N.
Если бы было разрешено использовать 5 или 6 цветов, или если бы карте нужно было только 2 цвета, то эффективные алгоритмы были бы известны.
Еще одна возможность получить эффективный метод состоит в том, чтобы отказаться от требования о том, что алгоритм ВСЕГДА эффективен. Такая эвристика (т.е. набор инструкций), которая работает по крайней мере во многих случаях, будет рассмотрена ниже:
- Полезно сначала раскрасить область, которая имеет как можно больше соседей, потому что если эта область получит цвет А, то все ее соседи получат ограничение не получить цвет А. Это уменьшает количество вариантов цвета для этих соседних областей и, таким образом, уменьшает количество последующих попыток, если раскрашивание оказывается сложным.
- Цвет, использованный в самом первом окрашивании, определенно бесплатный.
- В первый раз, когда для раскрашивания области используется второй цвет, этот выбор цвета свободен, если эта область соприкасается с областью первым цветом, т.е. если необходим второй цвет.
- В первый раз, когда для раскрашивания региона используется третий цвет, этот выбор цвета свободен, если этот регион касается региона первым цветом и региона вторым цветом, т.е. если необходим третий цвет.
- Мы должны раскрасить область, для которой остался только один возможный цвет, чтобы мы не могли ошибиться в этой раскраске.
- Количество попыток раскрашивания определенно меньше 4N (пробуя все 4 цвета для всех N регионов). Таким образом, это количество попыток раскрашивания критически зависит от количества регионов N. Следовательно, это полезно, если раскраска разбивает белую (неокрашенную) часть карты на отдельные, разрозненные белые подкарты, которые затем могут быть раскрашены сами по себе. Эти регионы имеют только N1 и N2 регионы (N = N1 + N2), и теперь им требуется не более 4N1 + 4N2 попыток, что намного меньше, чем 4N1 × 4N2 = 4N попыток.
- Если кто-то хочет найти наименьшее количество цветов, которые могут раскрасить данную карту, то сначала нужно проверить, достаточно ли 2 цветов. Это можно сделать эффективно.
Если необходимо использовать только два цвета A и B и один из регионов уже имеет цвет, то обход точки пересечения фиксирует цвет всех остальных регионов: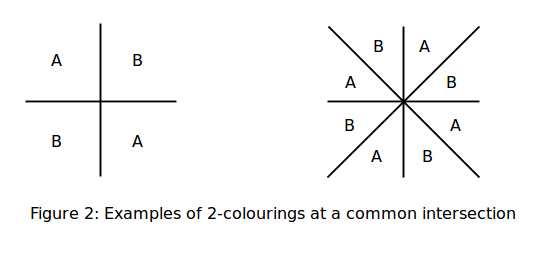
Это правило также полезно для первой попытки раскраски карт, которым требуется 3 или 4 цвета. Например, если область 1 ниже уже имеет цвет А, то области 2 и 4 нуждаются в другом цвете, и мы понятия не имеем, что это может быть, но мы знаем, что раскрашивание области 3 цветом А не создает дополнительных условий для раскрашивания областей 2 и 4, потому что у них уже есть сосед цвета А. На рисунке 3 показана лишь небольшая часть карты, но приведенная выше эвристика может быть более точным для любой карты.
Если все соседи области 3 (на рисунке 3, области 2 и 4) имеют хотя бы одного соседа цвета А (на рисунке 3, область 1), то раскрашивание области 3 цветом А не может быть ошибкой. Причина в том, что раскрашивание области 3 с A не создает никаких новых ограничений для ее соседей, потому что им уже запрещено иметь цвет A. Так что если в процессе дальнейшего окрашивания окажется, что была допущена ошибка (потому что количества цветов недостаточно), то нет смысла давать региону 3 другой цвет, а не А, нужно попробовать еще какую-то раскраску. - Что, если область 3 выше также является диагональным соседом другой области, скажем, области 9, которая уже имеет другой цвет, например, цвет B? Должен ли 3 быть окрашен в цвет А или В? Также здесь полезно проверить всех соседей 3, запрещено ли им уже иметь цвет А или запрещено иметь цвет В. Если ни то, ни другое не так, то мы можем подождать с раскраской 3.






Следите за обновлениями или подписывайтесь на них: