Chomp ©

Поле — це перехресна точка рядка та стовпця, позначена (рядок, стовпець).
Плитка - це зображення на деяких полях.
Позиція складається з усіх полів з плитками.

Почнемо з легких проблем, тобто невеликих позицій. Щоб створити їх, ми натискаємо «Комп'ютер: Вимкнено». Якщо ми потім натиснемо на (2,1) залишиться тільки один ряд плиток.

Що може наступний гравець, тобто ваш суперник, зробити?
- Натиснувши на (1,2), залишається тільки плитка на (1,1), тому ви програли.

Потім давайте натиснемо «Нова гра» і далі (3,1) і (2,2), щоб мати одну плитку в рядку 2 і всі рядки 1.

Що може зробити наступний гравець?
- При натисканні на (1,3) залишається тільки три плитки. Чи бачите, що у вас немає можливості?

Давайте натиснемо на «Нову гру» та натиснемо на (3,1) та (2,3).

Що може зробити наступний гравець?
- Ваш опонент може натиснути на (1,4). Чи бачите, що у вас немає можливості?

Чи можете ви підсумувати, в яких позиціях з плитками тільки в 2 рядах у вас немає можливості виграти гру?
- Якщо верхній ряд має на одну плитку більше ніж 2-ий ряд, то що б ви не робили, ваш опонент завжди може зробити хід так, щоб у верхньому ряду було на одну плитку більше, ніж у 2-му. Тоді незалежно від того, що ви робите, в решті решт вам потрібно буде вибрати плитку (1,1) і програти гру.

Якщо натиснути плитку , то всі плитки знизу та праворуч також видаляються. Це правило має симетрію; тобто вся гра має наступну симетрію: Якщо ми обмінюємося рядками та стовпцями, то правило залишається незмінним: усі плитки праворуч стають усіма плитками знизу, а всі плитки знизу стають усіма плитками праворуч від видаленої плитки. Іншими словами, якщо ми віддзеркалюємо позицію вздовж лінії, що проходить (1,1) і (2,2), то нова позиція може виглядати інакше , але вона має однаковий статус. Переможний хід також буде таким же ходом, тільки дзеркальним.

Позиція з 3 плитками в першому ряду і 2 плитками в другому ряду безнадійна, як ми знаємо. Які плитки мають дзеркальні положення?
- Після дзеркального відображення він має 3 плитки в лівій колонці і 2 плитки в 2-й колонці.

Ми знаємо всі безнадійні позиції, що мають плитку тільки в перших двох рядах. Що говорить нам симетрія про всі безнадійні позиціі з плитками тільки в перших двох колонках?
- Безнадійні позиції з плитками в перших двох колонках - це ті, де перша колонка має на одну плитку більше, ніж друга.

Ось ще одна позиція без можливості: натисніть на «Нова гра» та на (4,1), (2,2) і (1,4).

Якщо опонент робить хід на цій позиції, яка ваша відповідь?
- Потрібно переконатися, що після вашого ходу верхній рядок і перший стовпець знову мають однакову довжину. Повторивши цю закономірність, суперник в підсумку змушений буде взяти плитку (1,1) і програти.

Отже, якщо перший рядок і перший стовпець мають однакову кількість плиток, а інших плиток немає, то позиція безнадійна. Які позиціі можуть бути змінені на таку позицію?
- Якщо позиція має однакову кількість рядків і стовпців, незалежно від того, скільки плиток є де-небудь ще: перехід на (2,2) залишає тільки перший рядок і перший стовпець однакової довжини, не залишаючи супернику можливості. Отже, якщо позиція має таку ж кількість плиток у верхньому рядку, як і в лівому стовпці, тоді ви граєте на (2,2) і виграєте гру.

Щоб добре зіграти в Чомпі, потрібно знати про виграшні і програшні позиції . Виграшна позиція - це та, де можна забезпечити перемогу, якщо одна грає оптимально, незалежно від того, що робить інша сторона. Програшна позиція - це та, де у однієї немає можливості, якщо інша сторона грає оптимально. Наступні моменти - це те, що називають в математиці визначенням. У Чомпі програшні та виграшні позиції визначаються через ці 3 бали:
1. Якщо залишилася тільки одна плитка (у верхньому лівому куті), то це програшна позиція.
2. Позиція є виграшною позицією, якщо існує хід, який призводить до програшної позиції для суперника.
3. Позиція є програшною позицією, якщо кожен хід призводить до виграшної позиції для суперника.
На перший погляд вищенаведені пункти можуть виглядати марними, оскільки виграшні позиції пояснюються програшними позиціями, а програшні позиції пояснюються виграшними позиціями. Тим не менш, визначення базується на виконанні ходів, і кожна послідовність ходів в кінцевому підсумку призводить до позиціі однієї плитки, яка відповідно до пункту 1 є програшною позицією.

Чи можливо, що є такі позиції, де жодна із сторін не може забезпечити перемогу? (складно)
- Сформулюємо невелику теорему і доведемо її. Доказ покаже нам, яким шляхом можна досягти ідеальної ігрової сили. Доведення є доказом шляхом індукції, де показується, що твердження, яке ми хочемо довести, є істинним для одного сегмента, а потім показує, що якщо воно вірне для будь-якого числа N плиток, то воно також має бути вірним для ще однієї плитки, тобто N+1 плитки. Оскільки це твердження вірне для плитки N=1, воно повинно бути вірним для N+1=1+1=2 плиток. Але будучи вірним для N=2, він також повинен бути вірним для N+1=2+1=3 плиток і так далі; тобто для будь-якої кількості плиток.
- Лемма (мала теорема): Кожна позиція є або виграшною, або програшною.
- Доведення індукцією:
- Індукційна основа: Якщо позиція має лише одну плитку, то ця плитка знаходиться у верхньому лівому куті, а потім позиція є програшною позицією за правилом Chomp (показуючи, що лема вірна, якщо присутня лише плитка N=1).
- Індукційна гіпотеза: Ми припускаємо, що лема вірна для всіх позицій до N плиток, тобто позицій з 1,2,..., N плитки або виграють, або програють позиції.
- Крок індукції: Тепер ми хочемо показати, що тоді також усі позиції з плитками N+1 повинні бути або програшними, або виграшними.
- У наступному, P є в довільному положенні з N+1 плитками. Якщо P зменшується на один хід, то нова позиція повинна мати ≤N плиток, тому це програшна або виграшна позиція відповідно до індукційної гіпотези. Якщо P можна зменшити за один хід до програшної позиції, то P є виграшною позицією. Якщо немає, то Р можна знизити за один хід тільки до виграшної позиції. Але якщо позиція може бути зменшена в русі лише до виграшної позиції, то P повинна бути програшною позицією. Це доводить, що P (маючи плитки N+1) є або виграшною, або програшною позицією. Це показує, що всі позиції (з N+2,N+3,... плитки) є або виграшними, або програшними позиціями.
  
  Кінець доказу ∎
- Додатковий коментар: Крок індукції забезпечує метод вирішення для всіх позицій (до певного розміру), виграють вони чи втрачають позиції. Вона визначається наступним:
  
  Один починається з N=1 і позначає цю позицію як програшну позицію. Потім один визначає статус всіх позицій за допомогою 2 плиток, потім з 3 плитками і так далі, кожен раз використовуючи знання про статус менших позицій, і додаючи знову знайдену програшну позицію в список відомих програшних позицій.
- Це дуже ефективний спосіб знайти всі виграшні та програшні позиції до певного розміру. Оскільки цифри стають більшими за розміром, комп'ютерна програма буде корисною. Необхідні інгредієнти наступні:
  - Процедура, яка може ефективно створювати всі позиції N плиток від знання всіх положень менше N плиток
  - Процедура, яка може ефективно перевірити, чи можна звести позицію до іншої заданої позиції.
  Ми залишимо це для вас: подумайте про це докладніше і, можливо, створіть таку комп'ютерну програму.

Скільки програшних і виграшних позицій має рівно 2 плитки?
- Є лише два можливих положення, які мають рівно 2 плитки, 2 плитки у верхньому ряду або дві плитки вздовж лівого стовпчика. Обидві ці позиції є виграшними.

Скільки програшних і виграшних позицій має рівно 3 плитки?
- Всього можливих позицій 3, які мають рівно 3 плитки. Вони складаються з 2 виграшних позицій, і 1 програшної позиції. Чи можете ви розібратися, на яких позиціях вони знаходяться?

Скільки програшних і виграшних позицій мають рівно 4 плитки?
- Є 5 можливих положень, які мають рівно 4 плитки. Всі ці позиції є виграшними позиціями.

Скільки програшних і виграшних позицій має рівно 5 плиток?
- Всього можливих позицій 7, які мають рівно 5 плиток. З цих позицій 3 втрачають позиції і 4 - виграшні. Чи можете ви зрозуміти, які вони?

Прямокутні позиції виграють чи програють?
- На це питання відповідає наступна лема. Доказ є доказом існування. Це лише доведе існування виграшного ходу, не показавши, що це за хід. Тим не менш, знання леми корисно для вашої гри, як пояснено нижче.
- Лема: Всі прямокутні позиції, крім позиції 1-плитки, є виграшними позиціями.
- Доказ: Щоб показати, що це правда, нам потрібно розглянути два можливих випадки:
  1. Видалення плитки в правому нижньому кутку дошки - виграшний хід.
  2. Видалення плитки в правому нижньому кутку не є виграшним ходом.
- Якщо випадок 1 вірний, то це означає, що прямокутник є виграшною позицією, і це підтримує лему.
- Якщо випадок 1 не відповідає дійсності, то потрібно розглянути випадок 2. Згідно з доказом, який ми робили раніше, позиція, отримана в результаті видалення плитки в правому нижньому куті, повинна бути виграшною позицією, а це означає, що вона повинна мати виграшний хід, який існує. Але, оскільки кожен хід в прямокутнику знімає плитку в правому нижньому кутку, положення програшу, отримане в результаті 2-го ходу (виграшного ходу), однакове, незалежно від того, чи виконується виграшний хід після переміщення кута або замість кутового переміщення. Це означає, що переможний хід можна було зіграти відразу, тим самим довівши, що для прямокутної позиції існував виграшний хід.
- Кінець доказу ∎
- Додаткові коментарі: Хоча лема не говорить нам, що таке виграшний хід, вже корисно знати, що прямокутні позиції є виграшними позиціями. Тому не слід робити рух, який створює прямокутне положення (за винятком положення 1x1).

Чи можете ви визначити для будь-якої квадратної дошки, що таке виграшний хід?
- Для всіх квадратів розміром >1 єдиним виграшним ходом є (2,2).

Для яких позицій, схожих на квадрат, той самий хід є виграшним ходом?
- Хід (2,2) також є виграшним ходом для будь-якої позиції, де 1-й рядок і 1-й стовпець мають однакову довжину.

Чи може позиція мати більше одного виграшного ходу?
- Так, позиція може мати більше, ніж один виграшний хід. Врахуйте наступну позицію:
  
  ###
  ##
  #
  
  Ця позиція ради має 3 різні виграшні ходи, які можна зробити. Чи можете ви визначити, що вони собою являють?

Загальна стратегія перемоги на Чомп полягає в тому, щоб створити програшні позиції для свого суперника, щоб у нього не було можливостей.Ми також хочемо уникнути створення виграшних позицій, які суперник може перетворити на програшні для нас позиції.

Ключ до перемоги полягає в тому, щоб знати якомога більше програшних позицій і виявити, як створити їх до того, як це зробить ваш опонент. Розглянемо наступну можливу дошку, яка є відомою програшною позицією:

#######
###
###
#
#
Малюнок 1

Які всі позиції можна перетворити в цю програшну позицію за один хід?

Вищевказана програшна позиція може бути результатом будь-якого переміщення, позначеного знаком + нижче:

#######+
###
###
#
#

#######
###+
###
#
#

#######
###
###
#+
#

#######
###
###
#
#
+

Малюнок 2

Всі ці ходи розташовані у вирізаних кутах. Будь-який такий рух + також вирізає плитки, які можуть з'явитися на зображеннях нижче з ?:

#######+?
###
###
#
#

#######
###+???
###????
#
#

#######
###
###
#+?
#??

#######
###
###
#
#
+
?

Малюнок 3

Плитка + необхідна, а ? плитка необов'язкова. У лівій виграшній позиції верхній ряд може бути витягнутий довільно вправо з більшою кількістю '?', а в правій виграшній позиції перший стовпець може бути витягнутий довільно до низу з більшою кількістю '?'. Всі ці позиції також є виграшними позиціями. Якщо ми хочемо зробити хід в такому положенні, ми візьмемо + плитку, а значить і все ? Підключені плитки також будуть видалені, в результаті чого втрачається позиція, з якої ми почали.

Чи є більше виграшних чи більше програшних позицій?
- Для кожної програшної позиції існує нескінченно багато позицій, які можна перетворити в цю програшну позицію одним ходом. Тому всі ці нескінченні позицій є виграшними.
- Тому виграшних позицій набагато більше, ніж програшних. Тому найефективніше запам'ятати якомога більше програшних позицій, всі інші позиції є виграшними.

Складіть список програшних позицій, які вам відомі, і по кожній позиції запишіть всі відповідні виграшні позиції і як їх виявити

Наступний приклад показує, що ми маємо на увазі:

Як було показано раніше, коли позиція має всього 2 рядки, а верхній ряд має на одну плитку більше, ніж другий ряд, то це програшна позиція, як показано нижче:

#####
####
Займаючи цю відому програшну позицію, можна визначити, що відповідними виграшними позиціями є:

#####+?
####

#####
####+

#####
####
+???
????

У лівому положенні може бути будь-яка кількість ? праворуч від верхнього ряду, а в правильному положенні може бути будь-яка кількість рядів ? під. Ми можемо підсумувати словами, як виявити ці виграшні позиції (які ви повинні запам'ятати для своєі гри):

- Позиція - це виграшна позиція, яка зводиться до
  #####
  ####
- - Якщо та чи інша позиція має тільки два ряди, а перший ряд не зовсім довший на одну плитку, ніж другий ряд, або
- - Якщо позиція має більше двох рядів, і перший ряд рівно на одну плитку довший, ніж другий ряд.
Але є над чим подумати. Ми не тільки хочемо правильно грати на таких виграшних позиціях, ми також хочемо уникнути ходу, який створює такі виграшні позиції. Це означає, що ми не повинні робити хід там, де залишається тільки два ряди, або де другий ряд має рівно на одну плитку менше, ніж перший ряд.

Підводячи підсумок, ми хочемо створити програшні позиції, але ми також хочемо уникнути створення позицій, які є одним відходом від програшної позиції.

Ще слід зазначити: через згаданої раніше дзеркальної симетрії всі перераховані вище коментарі можна повторити, просто замінивши слово «рядок» словом «колонка».

Вам залишається зібрати більше програшних позицій та відповідних їм виграшних позицій, які є одним відходом.

Що робити, якщо вам доведеться грати на програшній позиції?
- Якщо ви усвідомлюєте, що вам належить зробити хід в програшній позиції, то в теорії у вас немає шансів. Все, що ви можете зробити, це сподіватися, що ваш опонент не знає всіх виграшних ходів для позицій, які ви можете створити своїм наступним ходом. Що ви могли зробити, так це видалити лише одну плитку з кута. Це дає вашому опоненту отриману позицію максимального розміру, і це ускладнює для вашого опонента знання відповідного виграшного ходу.

Як навчитися втрачати позиції самостійно?
- Потрібно було б виконати те, що називається повним пошуком дерева. Перший гравець починає з вгадування ходу, потім другий гравець вгадує хід і так до тих пір, поки один гравець, скажімо, гравець А, не виграє. Тоді гравцеві B дозволяється змінити останній хід, який вони зробили, і це черга гравця А. Якщо на одній позиції у гравця, що грає поруч, скажімо В, закінчуються ходи, тому що всі ходи призводять до програшу, то це програшна позиція, і гравець В може змінити останній хід, зроблений до того, як ця програшна позиція була досягнута.
- Цей «пошук дерева» триває до тих пір, поки не з'ясується, чи є вихідна позиція програшною або який хід гравця 1 перетворює його в програшну позицію.
- Це може бути дуже тривалим процесом, якщо спробувати зробити це на початковій дошці з багатьма плитками. Однак чим більше втрачаючих позицій ми знаємо, тим коротше послідовності ходів до досягнення такої позиції, і, таким чином, весь пошук відбувається набагато швидше. Якби ми знали, що всі містять програшні позиції, то або вихідна позиція була б визнана програшною, або для зведення її до програшної позиції був би необхідний тільки один хід.

Як навчитися втрачати позиції за допомогою комп'ютера?
- На рівні складності «Дуже важко» і позиціях не більше 8 х 15 комп'ютер грає ідеально, тому кожна позиція, що виникає в результаті переміщення комп'ютера, є програшною постіоном! Починати слід з дуже маленьких дощок і грати проти комп'ютера на рівні "Very Hard" і вивчати всі позиції, які генерує комп'ютер. Для кожної такої позиції подумайте, як на кожен ваш хід відповість комп'ютер, перетворивши його знову в меншу програшну позицію. Для кожної програшної позиції також дзеркальне положення (рядки <--> стовпців) є програшною позицією.
- Що є оптимальним першим ходом?
  - У конкурсі стартовою позицією буде прямокутник цукерок. Як було доведено раніше, прямокутник - це виграшна позиція, але який перший хід змінює його в програшну для суперника позицію? Раніше ми дізналися, що оптимальним ходом для квадрата є плитка (2,2), але що робити, якщо прямокутник не є квадратом?
  - Просто перейдіть на «дуже жорсткий» рівень складності і дозвольте комп'ютеру зробити перший крок. Поки прямокутник не більше 8х15, комп'ютер працює оптимально і покаже ідеальний перший хід. Спробуйте різні розміри прямокутників і запам'ятайте оптимальний перший хід, оскільки комп'ютерна гра буде недоступна в дні змагань :).
- Незабаром ви будете неперевершені в легкому і середньому рівні складності.

Чи існують нескінченні сім'ї втрат позицій?
- Ми вже зустрічалися з цими двома сім'ями програшних позицій. N - будь-яке додатне ціле число.
- Ось ще:

Вбудований в гру комп'ютерний гравець використовує різні прийоми для різних ігрових рівнів.

- легкий- Робить випадкові ходи на кожному кроці. Якщо буде виявлена проста виграшна позиція, вона переміститься туди.
- Середнє- Як і раніше рухається хаотично, але володіє більшими знаннями про виграшні і програшні позиції. Дозволить уникнути ходів, які дають супернику доступ до простого виграшного ходу.
- Жорсткий- Має ще більші знання про виграшні позиції. Активно шукає на дошці ходи, які можуть змусити суперника самим зробити програшний хід.
- Дуже важко - Завжди зробить оптимальний хід для будь-якого положення, яке поміщається в прямокутник розміром 8х15.
Чим вище рівень складності, тим складніше буде змусити комп'ютер в програшне положення. Кожен рівень знає набагато більше виграшних і програшних позицій, ніж попередній рівень, і чим важче складність, тим більше виграшних і програшних позицій вам потрібно буде знати, щоб спробувати змусити комп'ютер в програшну позицію.

Наступні коментарі не допоможуть зміцніти в Чомпі, але вони нададуть деякі цікаві факти і дадуть нам ще одну можливість для практики доказів шляхом індукції.

Скільки різних позицій, включаючи порожню дошку, вміщується в прямокутник з рядками P і стовпцями Q?
- Якщо включити порожній прямокутник, то можна обчислити загальну кількість можливих позицій за такою формулою: $\frac{(P+Q)!}{P!Q!}$ Чи можете ви обчислити це число для невеликих P і Q і переконатися, що воно правильне?
- Перше виведення рекурсивної формули
  - Нехай f(P,Q) — кількість позицій у прямокутнику розміру PxQ. Важливим спостереженням є те, що всі позиції мають форму сходів, де кожен ряд має щонайбільше стільки плитки, скільки ряд вище, але не більше.
  - Давайте спочатку почнемо з того, як ми можемо представити всі ці сходи. Один із способів легко створити сходи - почати з лівого нижнього кута дошки, і рухатися або вправо, або вгору. Можна продовжувати робити ці правильні рухи вгору, поки вони не потраплять у верхній правий кут дошки. Ми будемо називати це шляхом, який ми пройшли, щоб дістатися від (P,0) до (0,Q).
  - Кількість позицій така ж, як і кількість шляхів від (P,0) до (0,Q), якщо дозволяється рухатися лише вгору або вправо. Число f(P,Q+1) шляхів для переходу від (P,0) до (0,Q+1) є числом f(P,Q) шляхів, які потрібно отримати від (P,0) до (0,Q), а потім до (0,Q+1) + число f(P-1,Q) шляхів, щоб дістатися від (P,0) до (1,Q), а потім до (1, Q+1) і (0,Q+1) і так далі. Відповідна формула виглядає наступним чином: $f(P,Q+1) = f(P,Q) + f(P-1,Q) + f(P-2,Q) + \ldots + f(1,Q) + f(0,Q)$
  - Ми зараз візьмемо цю формулу і замінимо Р на Р + 1. Якщо замість P включити в формулу P + 1, отримаємо наступне: $f(P+1,Q+1) = f(P+1,Q) + f(P,Q) + f(P-1,Q) + \ldots + f(0,Q)$ $f(P+1,Q+1) = f(P+1,Q) + f(P,Q+1)$ З цього нового виведення ми можемо визначити формулу $f(P,Q) = f(P,Q-1) + f(P-1,Q)$ де $f(P,0) = 1$ і $f(0,Q) = 1$ .
- Альтернативне виведення рекурсивної формули
  - Часто існує кілька способів підрахунку в комбінаторних задачах. Наступне виведення забезпечить інший і більш елегантний спосіб виведення формули.
  - Ми будемо використовувати те саме уявлення, яке ми використовували раніше, де ми хочемо знайти загальну кількість шляхів, які ведуть нас від (P,0) до (0,Q). Ми можемо організувати ці шляхи у дві групи.
  - Шляхи, які починаються з першого переміщення, що йде вправо від (P,0) до (P,1). Ми знаємо, що в цій групі ми будемо мати в цілому шляхи f(P,Q-1) від (P,1) до (0,Q). Ми знаємо це тому, що залишився прямокутник після переміщення один вправо має розмір P x (Q-1).
  - Інша група - це шляхи, які починаються з першого ходу, що йде вгору на один хід від (P,0) до (P-1,0). У цій групі ми знаємо, що є f(P-1,Q) сумарні контури, оскільки отриманий прямокутник буде розміром (P-1) x Q.
  - Тому, оскільки кожен можливий шлях потрапить в одну з цих двох груп, загальна кількість шляхів є сумою цих груп. Це дає нам ту саму формулу $f(P,Q) = f(P,Q-1) + f(P-1,Q)$ .
- Виведення явної формули
  - Замість того, щоб починати контури з правого нижнього кута, давайте повернемо прямокутник таким чином, щоб точка (P,0) була вгорі. Тепер ми можемо візуалізувати шляхи за наступною схемою:
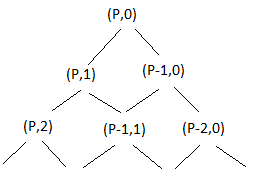
  - Цей тип діаграм відомий як дерево. Ця закономірність буде продовжувати повторюватися, поки ми не пройдемо шлях від (P,0) до (0,Q). Коли це станеться, дерево міститиме всі можливі шляхи, якими можна буде пройти через дошку.
  - Кількість способів потрапити з вершини (P,1) до вузла (I,J) в цьому дереві - це кількість способів дістатися до (I-1,J), а потім спуститися праворуч до (I,J), плюс кількість способів дістатися до(I,J-1), а потім спуститися вліво до (I,J). Іншими словами, це число в трикутнику Паскаля.
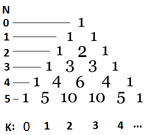
  - Кожне число в трикутнику Паскаля є сумою двох чисел вище. Цифри в лівому стовпці - це підрахунок рядків дошки, починаючи з 0 з порожньою дошкою. Цифри нижче трикутника представляють положення зліва, також починаючи з 0. Число в N'му рядку в позиції K дорівнює ${N \choose K} = \frac{N!}{(N-K)!K!}$ .
  - Ми хочемо знайти число f(p,q), яке є кількістю способів дістатися від (P,0) до (0,Q). Для цього потрібно йти від верхнього P разів вниз вправо, а Q разів вниз ліворуч. Використовуючи структуру дерева, яку ми визначили раніше, це те ж саме, що йти від (0,0) до (P,Q), що йде тільки вліво і вправо на дереві.
  - Однак це змушує нас робити кроки P+Q, тому ми знаходимося в ряду P+Q на дереві. Оскільки ми знаємо, що ми перемістили Q разів вправо, число в трикутнику Паскаля в цій позиції є ${P+Q \choose Q} = \frac{(P+Q)!}{P!Q!}$ .
- Доведення явної формули за допомогою індукції
  - Ми збираємося показати, що наступні формули еквівалентні. $f(P,Q) = \begin{cases}1 & for & P=0 \\1 & for & Q=0 \\f(P,Q-1) + f(P-1,Q) & for & \text{P>0 and Q>0}\end{cases} = \Bigg\{{P+Q \choose Q} = \frac{(P+Q)!}{P!Q!}$
  - Індукційна основа: Ми вже знаємо, що f(0,0) = 1 за визначенням формули. Якщо включити в формулу P=0 і Q=0, отримаємо $\frac{(0+0)!}{0!0!} = \frac{0!}{1} = 1$ . Це показує, що базові формули рівнозначні, що закінчує індукційну основу.
  - Індукційна гіпотеза: Припустимо, що формули еквівалентні для всіх значень P,Q з P+Q = N.
  - Крок індукції: Використовуючи індукційну гіпотезу, доведемо еквівалентність для всіх значень P,Q з P+Q=N+1. Для будь-яких значень P,Q з P+Q=N+1 маємо 3 випадки:
  - Випадок 1:
  - Випадок 2:
  - Випадок 3: $P,Q > 0$ $\begin{align} f(P,Q) &= f(P,Q-1) + f(P-1,Q)\qquad\qquad (+)\\ &= \frac{(P+Q-1)!}{P!(Q-1)!} + \frac{(P-1+Q)!}{(P-1)!Q!}\\ &= \frac{(P+Q-1)!Q}{P!(Q-1)!Q} + \frac{(P-1+Q)!P}{(P-1)!PQ!}\\ &= \frac{(P+Q-1)!}{P!Q!} (Q+P)\\ &= \frac{(P+Q)!}{P!Q!} \end{align}$
  - (+): Якщо P + Q = N + 1, то P + Q-1 = N, тобто за індукційною гіпотезою.
    f(P,Q-1) = $\frac{(P+(Q-1))!}{(P!(Q-1)!)}$ , і аналогічно для f(P-1, Q)
  - Це свідчить про те, що дві формули для f(P,Q) є еквівалентними.
  - Кінець доведення. ∎

Скільки різних позицій мають рядки P і стовпці Q?
- Можна просто використовувати одну і ту ж формулу для всіх позицій, що вписуються в прямокутник з рядками P-1 і стовпцями Q-1, що є f(P-1,Q-1).

Чи є більше виграшних чи більше програшних позицій?

# плитки	# позицій	# втрати позицій	% втрачених позицій
20	627	42	6.69
30	5604	220	3.92
40	37338	1022	2.73
50	204226	4976	2.43
60	966467	20106	2.08
70	4087968	76688	1.87
80	15796476	270142	1.71
90	56634173	897964	1.58

Гіпотеза Карибу

Раніше ми показували, що кожна позиція є або виграшною, або програшною. Доказ дав нам прямий метод визначення крок за кроком для всіх позицій, програють вони чи виграють. Особливим було те, що цей метод не потребував будь-якого пошуку (випробуванні ходів). Це нагадало нам «Решето Ератосфена», щоб визначити всі прості числа до певного розміру.

Читайте про сито Ератосфена, наприклад в інтернеті
- Щоб знайти всі прості числа до розміру N², де N – це деяке ціле число, виконайте такі дії:
- - A: Почніть з простого числа p=2.
  - B: Викреслити всі кратні p до N².
  - С: Знайдіть наступне найбільше число > p, яке ще не перекреслено. Якщо це число дорівнює > N, то алгоритм зупиняється. В іншому випадку зателефонуйте за цим номером p і продовжуйте крок B.
- Всі числа до N 2, які не перекреслені, є простими числами < N². Моделювання цього алгоритму можна знайти на https://en.wikipedia.org/wiki/Sieve_of_Eratosthenes

Ця аналогія надихнула нас на думку про більшу схожість між простими числами і втратою позицій. Це призвело до гіпотези втрати позицій, яка схожа на «Теорему про просте число». Ось деталі.

Таблиця: Аналогії між втратою позицій в chomp і простих числах:

Номери	Чомп
Цілих чисел нескінченно багато.	Позицій Чомпа нескінченно багато.
Є прості числа і факторизируемие числа.	Є програшні позиції і виграшні позиції.
Існує нескінченно багато простих чисел.	Втрачаючих позицій нескінченно багато.
Факторизоване число - це добуток простого числа і числа.	Виграшна позиція - це сума програшної позиції і позиції (тому що те, що вирізається в русі, має форму сходів, а тому є позицією).
Як тільки просте число відоме, людина миттєво знає нескінченно багато факторизованих чисел (всі кратні простому числу).	Після того, як програшна позиція відома, людина миттєво знає нескінченно багато виграшних позицій (всі позиції, що виникають в результаті заповнення кутових прямокутників, включаючи ті нескінченно довгі вздовж верхнього рядка та лівого стовпчика).
Велике число набагато частіше ділиться на мале просте число, ніж на велике просте число.	Велика позиція набагато частіше зводиться до невеликої програшної позиції, ніж до великої програшної.
Щоб визначити, чи є число N простим числом, дуже ефективно знати всі прості числа P до квадратного кореня N. Потім можна перевірити, чи можна N зменшити до P за поділом, тобто пробним поділом N / P.	Щоб визначити, чи є позиція P програшною, необхідно знати всі програшні позиції L, які містяться в P. Потім можна ефективно перевірити, чи можна зменшити P до L за один хід.
"Сито Ератосфена" - це ефективний спосіб визначити всі прості числа до деякого числа N, а також перевірити, чи є дане число простим числом. Даний алгоритм описаний вище.	Подібно до «Сита Ератосфена» починається з програшної позиції {1} і перекреслює всі виграшні позиції, які одним ходом зводяться до цієї програшної позиції. Потім один оглядає всі позиції ще однією плиткою. Всі позиції, які не перекреслені, втрачають позиції.
Решта неефективність ситового алгоритму полягає в багаторазовому закресленні факторізуемих чисел.	Решта неефективність ситового алгоритму полягає в багаторазовому закресленні виграшних позицій.
Щільність простих чисел зменшується з їх розміром; тобто відношення (# простих чисел до деякого цілого числа N) / N зменшується в міру збільшення N.	Щільність втрат позицій зменшується з їх розміром; тобто співвідношення (# втрачених позицій з до N плиток) / (# всіх позицій з N плитками) зменшується в міру збільшення N. (Завдання: Яка формула залежності цього співвідношення від N і як це порівнюється з формулою щільності простих чисел?).
Теорема про просте число: (# простих чисел ≤ N) / (N / log(N)) → 1 як N → нескінченність.	Аналогічна гіпотеза: (# втрати позицій з N плитками) / ((# позицій з N плитками) / log(# позицій з N плитками)) → 0,283... як N → нескінченність.

Таблиця: Відмінності між втратою позицій в Chomp і простими числами:

Номери	Чомп
Множина всіх цілих чисел являє собою повністю впорядковану множину; тобто між будь-якими двома числами людина знає, яка більша.	Множина всіх позицій Чомп є частково впорядкованою множиною. Позиціі можуть повністю міститися на інших позиціях, але не повинні.
Операцією по зменшенню числа до одного з його основних факторів є поділ.	Операція по зниженню положення до програшного положення - це віднімання плиток.
Число можна візуалізувати як відрізок прямої на одновимірній числовій лінії.	Позиція визначається через список чисел, відсортованих за розміром, і, таким чином, є 2D-об'єктом.

Відкриті питання:

Чи є гіпотеза (# втрати позицій з N плитками) / ((# позицій з N плитками) / log(# позицій з N плитками)) → 0,283... як N → нескінченність істинна?

Чи можете ви це довести? (Поки не можемо :-) )

Гра Чомп, в яку грали вище, є версією 2D Чомп. Це означає, що дошка всього 2-х габаритна, що має ширину і висоту.

Чи могли б ви уявити собі версію 3D Чомп?
- Найпростіший спосіб уявити собі додавання нового виміру в гру - це додавання третього виміру на дошку. Замість просто ширини і висоти нова дошка мала б довжину, ширину і висоту. Якби у когось були маленькі кубики, з якими можна було б грати, наприклад, гральні кістки, вони могли б грати в цю 3D-гру, як показано на малюнку нижче.
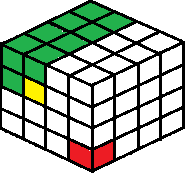
- Роблячи хід, можна було б видалити виділений кубик, а також кожен кубик ліворуч, вище і зверху від вибраного кубика. Зразок переміщення на зображенні підсвічується жовтим кольором, що також видаляє всі зелені сегменти на зображенні. Людина, яка бере останню плитку, показану червоною плиткою на зображенні, є гравцем, який програє гру.
- Щоб полегшити гру за допомогою справжніх кубиків, можна притиснути кубики до кута, наприклад, кута коробки для взуття, так що червона плитка знаходиться в самому кутку коробки, і доступна лише після того, як всі інші кубики також будуть видалені. Використовувати коробку не обов'язково, але це стабілізувало б кубики і полегшило б видалення кубика, не збиваючи всю конструкцію.

А як щодо гри в Чомп у ще більших вимірах?
- Раніше ми визначили, що досить легко додати новий вимір до гри Чомп. Якби хтось хотів грати в Чомп у ще більшому вимірі, ніж 3D, вони продовжували б додавати нові розміри до дошки Чомп. Однак після 3D вже немає можливості імітувати дошку Чомп за допомогою блоків. Однак існує спосіб імітації гри в Чомп за допомогою олівця та паперу, і цей метод дозволяє нам грати в гру в будь-якій кількості вимірів, а не тільки в 2D або 3D.
- Почнемо ми з гри в 2D Чомп на папері. Спосіб імітації гри полягає в тому, щоб спочатку вибрати число, яке має лише 2 різні прості множники. Наприклад, 72 = 2 3 х³ ². Потім запишемо всі фактори цього числа у вигляді прямокутника, як показано нижче.
- 72 36 18 9
  24 12 6 3
  8 4 2 1
- Будь-яке правосусіднє число менше на коефіцієнт 2, а будь-яке сусіднє число під ним менше на коефіцієнт 3. Щоб зробити хід на цій дошці, потрібно вибрати число. Потім ви видалите це число разом із будь-яким із його факторів. Той, хто візьме число 72, програє гру.
- Щоб мати більший початковий прямокутник, можна було знайти більше число, використовуючи формулу 2^P x 3^Q. Замінивши P і Q більшими числами, можна було б отримати більші та більші плати для 2D Chomp.
- Як можна узагальнити це моделювання для більш високих розмірів?
  - Щоб розширити цю олівцево-паперову версію Chomp з 2D до 3D, потрібно просто розширити формулу, яка використовується для пошуку початкового числа. Замість того, щоб вибирати число, яке має лише 2 різні прості множники, можна вибрати число, яке має 3 різні прості множники. Ми можемо використовувати нову формулу, щоб знайти це число, яке виглядає наступним чином: 2^P x 3^Q x 5^R. Потім, використовуючи ті ж методи, що і раніше, гру можна змоделювати в 3-х вимірах. Перехід до ще більших розмірів просто вимагає додавання нових простих чисел до формули, залежно від кількості вимірів, які ви хочете.