Chomp ©

Une case est un carreau formé à l’intersection d’une rangée et d’une colonne.
Une tuile est l’image qui apparaît dans quelques cases.
Une position comprend toutes les cases qui ont des tuiles.

Commençons avec des problèmes faciles, ç.-à-d. des petites positions. Pour les créer, on clique sur ‘Adversaire : Humain’ pour désactiver l’adversaire virtuel. Si on clique sur (2,1), il ne reste qu’une rangée de tuiles.

Que peut faire le joueur 2, votre adversaire?
- Si on clique sur (1,2), seule la tuile sur (1,1) reste, alors vous avez perdu.

Redémarrons et cliquons sur (3,1) et sur (2,2) de sorte qu’il reste une tuile dans la rangée 2 et toutes les tuiles dans la rangée 1.

Que peut faire l’adversaire?
- Si on clique sur (1,3), il ne reste que 3 tuiles. Pouvez-vous voir que vous avez perdu?

Redémarrons et cliquons sur (3,1) et sur (2,3).

Que peut faire l’adversaire?
- Votre adversaire peut cliquer sur (1,4). Pouvez-vous voir que vous avez perdu?

Pouvez-vous résumer dans quelles positions la partie est perdue quand il n’y a des tuiles que dans deux rangées du plateau?
- Si la première rangée a une tuile de plus que la deuxième rangée, il n’y a rien que vous pouvez faire pour empêcher votre adversaire de jouer de façon que la première rangée ait toujours une tuile de plus que la deuxième rangée. Quoi que vous fassiez, vous finirez par sélectionner (1,1) et vous perdrez.

Si on clique sur une tuile elle disparaît, ainsi que toutes les tuiles à droite et plus bas. Cette règle comporte une symétrie. C’est-à-dire le jeu entier comporte la symétrie suivante : si on échange les rangées et les colonnes, cette règle ne change pas ; toutes les tuiles à droite deviennent les tuiles en bas, et toutes les tuiles en bas deviennent toutes les tuiles à droite de la tuile supprimée. Autrement dit, si on trouve le symétrique d’une position réfléchie autour de l’axe qui passe par (1,1) et (2,2), la position résultante peut paraître différente, mais elle garde les mêmes propriétés. La position gagnante sera aussi la même, mais refléchie autour de cet axe.

On sait que la position avec 3 tuiles dans la première rangée et 2 tuiles dans la deuxième rangée est déjà perdue. Où sont les tuiles dans la position réfléchie?
- Après la réflexion autour de l’axe, il y a 3 tuiles dans la première colonne et 2 tuiles dans la deuxième colonne. Qu’est-ce qu’on peut conclure par rapport aux positions perdantes quand il n’y a des tuiles que dans les deux premières colonnes?

Alors on connaît toutes les positions perdantes n'ayant que des tuiles dans les deux premières rangées. Grâce à la symétrie, que peut-on déduire par rapport aux positions perdantes n'ayant que des tuiles dans les deux premières colonnes ?
- Les positions perdantes quand il n’y a des tuiles que dans les deux premières colonnes sont celles où la première colonne a une tuile de plus que la deuxième.

Voici une autre position perdante: Cliquez sur ‘Redémarrer’ et sur (4,1), (2,2) et (1,4).

Après le coup de votre adversaire, quelle est votre réplique?
- Vous devez vous assurer qu’après votre coup, la première rangée et la première colonne ont la même longueur. Si vous continuez à appliquer cette tactique, l’adversaire finira avec la tuile (1,1) et perdra.

Alors, si la première rangée et la première colonne ont le même nombre de tuiles et il n’y a pas d’autres tuiles, il est possible de s’assurer une victoire. Quelles positions peuvent devenir cette position?
- Si une position a le même nombre de rangées et de colonnes, quoi que soit le nombre de tuiles ailleurs : un coup sur (2,2) laisse la première rangée et la première colonne de longueur égale, ce qui assure une perte pour l’adversaire. Donc, si une position a le même nombre de tuiles dans la première colonne que dans la première rangée, il suffit de jouer un coup sur (2,2) pour gagner la partie.

Pour bien jouer à Chomp, il faut connaître les positions gagnantes et perdantes.Une position gagnante est celle où on peut s’assurer une victoire en jouant de façon optimale. Une position perdante est celle où vous ne pouvez pas gagner tant que l’adversaire joue de façon optimale. Les points suivants sont ce que l'on appelle en mathématiques une définition. Dans Chomp, on définit les positions gagnantes et perdantes par les critères suivants:
1. S’il ne reste qu’une tuile (dans la case supérieur gauche), alors c’est une position perdante.
2. Une position est gagnante s’il existe un coup qui donnera une position perdante à l’adversaire.
3. Une position est perdante si tous les coups donnent une position gagnante à l’adversaire.
À première vue, les critères ci-dessus peuvent avoir l’air inutiles parce que les positions gagnantes s’expliquent par des positions perdantes, et les positions perdantes s’expliquent par des positions gagnantes. Pourtant, la définition est fondée sur les coups joués, et toute séquence de coups termine par la position de la tuile unique, ce qui, selon le premier critère, est une position perdante.

Est-ce qu’il y a des positions où aucun joueur ne peut s’assurer une victoire? (niveau difficile)
- Pour traiter cette question, on va formuler un petit théorème et le démontrer. La démonstration nous montrera comment atteindre une force de jeu maximale. Cette démonstration sera une démonstration par recurrence où on montre qu’une déclaration que l’on veut démontrer est vraie pour une tuile et ensuite on montre que si elle est vraie pour n’importe quel nombre N de tuiles alors elle doit être vraie pour une tuile de plus, ç.-à-d. N+1 tuiles. Puisque cette déclaration est vraie pour N=1 tuile, elle doit être vraie pour N+1=1+1=2 tuiles. Mais puisqu’elle est vraie pour N=2 tuiles, elle doit être vraie aussi pour N+1=2+1=3 tuiles, et ainsi de suite, pour tout nombre de tuiles.
- Lemma (petit théorème): Chaque position est soit gagnante soit perdante.
- Démonstration par Induction :
- Initialisation: Si la position n’a qu’une tuile, alors cette tuile est dans le coin supérieur gauche et donc cette position est perdante selon les règles du jeu Chomp. (alors le lemma est vrai quand N=1 tuile est présente).
- Hypothèse: Nous disons que le lemma est vrai pour toutes les positions qui comportent jusqu’à N tuiles, ç.-à-d. les positions avec 1,2,…N tuiles sont soit gagnantes soit perdantes.
- Hérédité: Nous voulons montrer que toutes les positions comportant N+1 tuiles doivent être soit perdantes soit gagnantes.
- Soit P une position quelconque avec N+1 tuiles. Si on réduit P en jouant un coup, alors la nouvelle position doit comporter ≤N tuiles, donc elle est soit gagnante soit perdante selon l’hypothèse. Si on peut réduire P à une position perdante d’un coup, alors P est une position gagnante. Mais si on peut réduire une position à une position gagnante d’un seul coup, alors P doit être une position perdante. Cela démontre que P (comportant N+1 tuiles) est soit gagnante soit perdante. Cela démontre que toutes les positions (comportant N+2, N+3, …tuiles) sont soit gagnantes soit perdantes.
  
  Fin de Démonstration ∎
- Commentaire additionel: L’étape de l’hérédité fournit une méthode pour déterminer si toute position (jusqu’à une dimension donnée) est gagnante ou perdante. Elle se définit ainsi:
  
  On commence avec N=1 et on l’étiquette comme position perdante. Ensuite on détermine le statut de toutes les positions à 2 tuiles, à 3 tuiles, et ainsi de suite, se servant du statut connu des positions plus petites et ajoutant la position perdante la plus récemment identifiée à la liste des positions perdantes connues.
- Ceci est une façon très efficace de trouver toutes les positions gagnantes et perdantes jusqu’à une certaine dimension. Quand les nombres deviennent trop grands, un programme informatique sera utile. Il faudra les ingrédients suivants:
  - Une procédure qui peut créer de façon efficace toutes les positions avec N tuiles à partir des positions connues avec moins de N tuiles.
  - Une procédure qui peut vérifier de façon efficace si on peut réduire une position à une autre position donnée.
  C’est à vous de réfléchir à ce problème et éventuellement d’écrire un tel programme informatique.

Combien de positions perdantes et gagnantes comportent 2 tuiles?
- Il n’y a que 2 positions possibles qui comportent deux tuiles, 2 tuiles dans la première rangée ou 2 tuiles dans la première colonne. Elles sont toutes les deux gagnantes.

Combien de positions perdantes et gagnantes comportent 3 tuiles?
- Il y a 3 positions comportant 3 tuiles, dont 2 gagnantes et 1 perdante. Est-ce que vous pouvez identifier ces positions?

Combien de positions perdantes et gagnantes comportent 4 tuiles?
- Il y a 5 positions possibles comportant 4 tuiles. Toutes ces positions sont gagnantes.

Combien de positions perdantes et gagnantes comportent 5 tuiles?
- Il y a 7 positions possibles comportant 5 tuiles, dont 3 perdantes et 4 gagnantes. Est-ce que vous pouvez les identifier?

Les positions rectangulaires sont-elles gagnantes ou perdantes?
- Le lemme suivant répond à cette question. La démonstration est un théorème d’existence car il démontre l’existence d’un coup gagnant sans le donner. Pourtant, connaître ce lemma peut vous être utile pour jouer comme on explique ci-dessous.
- Lemme : Toutes les positions rectangulaires sont gagnantes à l’exception de la position comportant 1 tuile.
- Démonstration : Pour démontrer la vérité de cette declaration il faut considerer les deux cas possibles suivants:
  1. Retirer la tuile dans le coin inférieur droit est un coup gagnant.
  2. Retirer la tuile dans le coin inférieur droit n’est pas un coup gagnant.
- Si le cas 1 est vrai, alors le rectangle est une position gagnante, ce qui soutient l’hypothèse.
- Si le cas 1 n’est pas vrai, alors on doit considérer le cas 2. Selon la démonstration précédente, quand on enlève la tuile du coin inférieur droit, la position résultante est gagnante, ce qui veut dire qu’un coup gagnant existe. Pourtant, puisque tout coup joué sur un rectangle enlève nécessairement la tuile du coin inférieur droit, la position perdante donnée par le deuxième coup (le coup gagnant) est la même, peu importe si le coup gagnant suit le coup du coin ou à la place du coup du coin. Cela veut dire qu’on a pu jouer le coup gagnant depuis le début, démontrant ainsi qu’un coup gagnant existait pour la position rectangulaire.
- Fin de Démonstration ∎
- Commentaires additionnels: Bien que le lemme ne nous dise pas le coup gagnant, il est déjà utile de savoir que des positons rectangulaires sont des positions gagnantes. Il faut donc éviter de jouer un coup qui crée une position rectangulaire (à l’exception de la position 1x1, bien entendu).

Est-ce que vous pouvez identifier le coup gagnant pour tout plateau carré?
- Pour tous les carrés de largeur >1, le seul coup gagnant et sur (2,2).

Pour quelles positions ressemblant à un carré ce coup n’est-il pas un coup gagnant?
- Le coup (2,2) est un coup gagnant pour toute position où la première rangée et la première colonne ont la même longueur.

Est-ce qu’une position peut avoir plus qu’un coup gagnant?
- Oui, une position peut avoir plus qu’un coup gagnant. Considérez la position suivante:
  
  ###
  ##
  #
  
  Dans cette position, il y a trois coups gagnants possibles. Est-ce que vous pouvez les identifier?

En générale, la stratégie pour gagner à Chomp consiste de créer des positions perdantes pour votre adversaire pour qu’il ne puisse pas gagner. Il faut aussi éviter de créer des positions gagnantes que l’adversaire pourrait transformer en positions perdantes pour vous.

La clé de la victoire est de pouvoir reconnaître la plus de positions perdantes possibles, et de pouvoir détecter comment en créer avant votre adversaire. Considérons le plateau suivant qui montre une position perdante connue:

#######
###
###
#
#
Figure n°1

Quelles sont toutes les positions qui peuvent devenir cette position en un coup?

La position perdante ci-dessus peut résulter de tout coup indiqué par un + ci-dessous:

#######+
###
###
#
#

#######
###+
###
#
#

#######
###
###
#+
#

#######
###
###
#
#
+

Figure n° 2

Ces coups se trouvent tous dans les coins vides. Un tel + coup enleverait aussi toutes les tuiles représentées par ? ci-dessous :

#######+?
###
###
#
#

#######
###+???
###????
#
#

#######
###
###
#+?
#??

#######
###
###
#
#
+
?

Figure n° 3

Les tuiles + sont nécessaires, et les tuiles ? sont facultatives. Dans la position gagnante à gauche, on pourrait ajouter un nombre quelconque de ? à la première rangée, et dans la position gagnante à droite, on pourrait ajouter un nombre quelconque de ? à la première colonne. Toutes ces positions sont également gagnantes. Si on doit jouer un coup dans une telle position, nous prendrons une tuile +, alors toutes les tuiles ? connectées disparaîtront aussi, ce qui crée la position perdante dans laquelle nous avons commencé.

Y a-t-il plus de positions gagnantes ou perdantes ?
- Pour chaque position perdante, il existe un nombre infini de positions qui peuvent se transformer en cette position perdante par un seul mouvement. Tous ces positions infiniment nombreuses sont donc des positions gagnantes.
- Alors, il y a beaucoup plus de positions gagnantes que de positions perdantes. Par conséquent, il est plus efficace de se souvenir d'autant de positions perdantes que possible, toutes les autres positions étant des positions gagnantes.

Dressez une liste de toutes les positions perdantes que vous connaissez, et pour chaque position écrivez toutes les positions gagnantes correspondantes et comment les détecter

L’exemple suivant illustre cette méthode :

Comme l’on a déjà montré, quand une position n’a que deux rangées/colonnes, et que l’une a une tuile de plus que l’autre, celle-ci est une position perdante, comment on montre ci-dessous :

#####
####
À partir de cette position perdante connue, nous pouvons determiner que les positions gagnantes correspondantes sont :

#####+?
####

#####
####+

#####
####
+???
????

Dans la position à gauche, il peut y avoir n’importe quel nombre de ? à la droite de la première rangée, et dans la position à droit, il peut y avoir n’importe quel nombre de ? dessous. Nous pouvons résumons verbalement comment détecter ces positions gagnantes (dont ce serait utile de vous rappeler lors de vos parties futures):

- Une position est gagnante lorsqu'on peut la réduire à la position suivante
  #####
  ####
- - Soit si la position n’a que deux rangées et la première rangée n’est pas plus longue que la deuxième d’une seule tuile, soit
- - Si la position a plus de deux rangées, et que la première rangée est plus longue que la deuxième d’une seule tuile.
Il n’y a pas que ça à considerer. On ne veut pas seulement jouer de façon correcte dans de telles positions gagnantes, on veut aussi éviter de jouer un coup qui crée de telles positions gagnantes. Ceci veut dire qu’il ne faut pas jouer un coup ni quand seulement deux rangées en résulteront, ni quand la deuxième rangée n’aura qu’une tuile de moins que la première rangée.

Pour résumer, nous cherchons à créer des positions perdantes, mais nous voulons aussi éviter de créer des positions qui peuvent devenir une position perdante en un seul coup.

Une autre chose à noter : on peut remplacer le mot « rangée » par le mot « colonne » dans les commentaires ci-dessus qui restent valides grâce à la symétrie mentionnée en haut.

C’est à vous d’agrandir votre liste de positions perdantes et les positions gagnantes qui sont séparées d’un seul coup.

Et s’il faut jouer dans une position perdante?
- Si vous vous rendez compte que vous devez jouer un coup dans une position perdante, théoriquement vous n’avez aucune chance de gagner. Vous ne pouvez rien sauf espérer que votre adversaire ne connaît pas tous les coups gagnants pour les positions que vous pouvez créer avec votre prochain coup. Vous pouvez enlever une seule tuile d’un coin, comme ça vous donnez à votre adversaire une position résultante de dimension maximale, et ce sera plus difficile pour votre adversaire de choisir le coup gagnant correspondant.

Et si vous ne connaissez aucune position perdante?
- Il faudra faire ce qu’on appelle un arbre binaire de recherche. Le joueur A commence par choisir un coup, ensuite le joueur B choisit un coup et ainsi de suite jusqu’à ce qu’un joueur, disons joueur A, gagne. Ensuite le joueur B peut refaire son dernier coup avant le tour du joueur A. Si dans une position, un joueur à son tour n’a plus de coups qui restent à jouer car tous les coups entraînent sa perte, cela est donc une position perdante et donc le joueur B peut modifier le dernier coup joué avant d’atteindre la position perdante.
- Cet ‘arbre de recherche’continue jusqu’à ce qu’il soit clair que la position de depart est une position perdante qu’on identifie quel coup du joueur A a crée cette position perdante.
- Comme vous pouvez imaginer, ceci peut durer longtemps si on essaie de le faire avec un plateau de départ avec beaucoup de tuiles. Plus on connaît de positions perdantes, moins il faut jouer de coups avant d’atteindre une telle position, ce qui rend la recherche moins lente. Si on connaissait toutes les positions perdantes possibles pour un plateau donné, alors soit la position de départ serait reconnue comme perdante, soit il ne faudrait qu’un coup pour la réduire à une position perdante.

Comment apprendre les positions perdantes à l'aide de l'ordinateur?
- Pour le niveau de difficulté "Très Difficile" et les positions inférieures à 8 x 15, l'ordinateur joue de manière parfaite, de sorte que chaque position résultant d'un mouvement de l'ordinateur est une position perdante ! Il faut commencer avec de très petites grilles et jouer contre l'ordinateur au niveau "Très Difficile" et apprendre toutes les positions générées par l'ordinateur. Pour chacune de ces positions, pensez à la façon dont l'ordinateur répondrait à chacun de vos mouvements en le transformant à nouveau en une position perdante plus petite. Pour chaque position perdante, la position miroir (rangées <--> colonnes) est également une position perdante.
- Quel est un premier coup optimal ?
  - Lors du concours, la position de départ sera un rectangle de bonbons. Comme prouvé précédemment, un rectangle est une position gagnante, mais quel est le premier coup qui le transforme en position perdante pour l'adversaire ? On a appris plus tôt que le coup optimal pour un carré est la tuile (2,2) mais que se passe-t-il si le rectangle n'est pas un carré ?
  - Il suffit de basculer vers le niveau de difficulté "Très Difficile" et de laisser l'ordinateur faire le premier coup. Tant que le rectangle n'est pas plus grand que 8x15, l'ordinateur joue de manière optimale et montrera le premier coup parfait. Vous pouvez réessayer avec de différentes dimensions pour voir le premier coup optimal pour chaque grille de jeu, mais souvenez-vous du premier coup optimal car cette fonctionnalité ne sera pas disponible lors des jours de concours :).
- En ce faisant, vous deviendrez vite imbattable aux difficultés facile et moyenne.

Y a-t-il un nombre infini de familles de positions perdantes ?
- On a déjà rencontré ces deux familles de positions perdantes. N est tout entier positif.
- Encore quelques-unes :

L’adversaire virtuel compris dans le jeu se sert des techniques différentes selon le niveau de difficulté du jeu.

- Facile – Il joue des coups au hasard. S’il détecte une position gagnante simple, il la jouera.
- Moyenne – Il joue toujours au hasard, mais il a une meilleure connaissance des positions gagnantes et perdantes. Il évite les coups qui permettraient un coup gagnant simle à l’adversaire.
- Difficile – Il a une connaissance encore plus détaillée des positions gagnantes. Il cherche le plateau pour des coups qui obligeront l’adversaire à faire un coup perdant lui-même.
- Très Difficile - Il jouera toujours le coup optimal pour une position au-dedans des dimensions 8x15.
Plus le niveau de difficulté est haut, plus il est difficile d’obliger l’ordinateur d’entrer dans une position perdante. Chaque niveau connaît plus de positions perdantes et gagnantes que celui qui le précède. Plus le jeu est difficile, plus vous devez connaître de positions perdantes et gagnantes pour obliger l’ordinateur d’entrer dans une position perdante.

Les commentaires suivants ne vous aideront pas à améliorer votre force du jeu en Chomp, mais ils vous fourniront des faits intéressants ainsi qu’une occasion de plus pour pratiquer des démonstrations par induction.

Combien de positions différentes, y compris le plateau vide, pourrait-on voir dans un plateau qui mesure P rangées par Q colonnes?
- En comptant le rectangle vide, on peut calculer le nombre de positions possibles total avec la formule suivante: \[\frac{(P+Q)!}{P!Q!}\]Est-ce que vous pouvez utiliser la formule pour calculer ce nombre pour un petit plateau, et vérifiez qu’elle est correcte?
- Dérivation d'une Première Formule Reccursive
  - Soit f(P,Q) le nombre de positions dans un rectangle de dimensions PxQ. Il est important de constater que tous les plateaux ont la forme d’un escalier, où chaque rangée a au plus le même nombre de tuiles que la rangée là-dessus, mais jamais plus.
  - Commençons en trouvant un moyen de représenter ces escaliers. Un moyen facile de créer un escalier consiste de partir du coin inférieur gauche du plateau et de se déplacer soit à droite soit en haut. On peut continuer de faire ces déplacements à droite et en haut jusqu’à ce qu’on atteigne le coin supérieur droit du plateau. On les appelera un chemin qu’on a suivi pour aller de (P,0) à (0,Q).
  - Le nombre de positions est égal au nombre de chemins de (P,0) à (0,Q), tant qu’on ne puisse se déplacer qu’à droite et en haut. Le nombre f(P,Q+1) de chemins pour aller de (P,0) à (0,Q+1) est égal au nombre f(P,Q) de chemins pour aller de (P,0) à (0,Q) et ensuite à (0,Q+1) + le nombre f(P-1,Q) de chemins pour aller de (P,0) à (1,Q), et ensuite à (1, Q+1) et (0,Q+1), et ainsi de suite. La formule correspondante suit : \[f(P,Q+1) = f(P,Q) + f(P-1,Q) + f(P-2,Q) + \ldots + f(1,Q) + f(0,Q)\]
  - On prend ensuite cette formule et on remplace P par P + 1. Si on remplace P dans la formule par P + 1, ça donne la formule suivante: \[f(P+1,Q+1) = f(P+1,Q) + f(P,Q) + f(P-1,Q) + \ldots + f(0,Q)\] \[f(P+1,Q+1) = f(P+1,Q) + f(P,Q+1)\]De cette nouvelle dérivaion, nous pouvons déterminer la formule \(f(P,Q) = f(P,Q-1) + f(P-1,Q)\) où \(f(P,0) = 1\) et \(f(0,Q) = 1\).
- Une Dérivation Alternative d’une Formule Récursive
  - Souvent il y a plus qu’un moyen de compter dans un problème combinatoire. La dérivation qui suit fournira un moyen plus élégant de dériver la formule.
  - On utilise la même représentation qu’avant, où nous voulons trouver le nombre total de chemins qu’on peut suivre entre (P,0) et (0,Q). On peut classer ces chemins dans deux catégories.
  - Les chemins qui commencent avec un déplacement à droite de (P,0) à (P,1). On sait que dans cette catégorie il y aura un total de (f(P,Q-1)chemis de (P,1) à (Q,0). On le sait car le rectangle qui reste après un déplacement à droite mesure P x (Q-1).
  - L’autre catégorie contient les chemins commençant par un déplacement en haut de (P,0) à (P-1,0). Dans cette catégorie, on sait qu’il y a f(P-1,Q) chemins au total car le rectangle résutant mesure (P-1) x Q.
  - Alors, car tout chemin possible se classe dans une de ces categories, le nombre total de chemins égale la somme de ces catégories. Ce qui nous donne la même formule \(f(P,Q) = f(P,Q-1) + f(P-1,Q)\).
- Dérivation d’une Formule Explicite
  - Au lieu de commencer nos chemins au coin inférieur droit, tournons le rectangle pour que le point (P,0) soit en haut. Nous pouvons alors visualiser les chemins en servant du diagramme suivant:
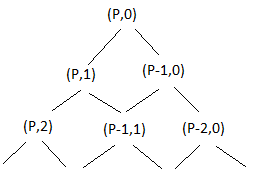
  - On appelle un tel diagramme un arbre. Le motif se répétera jusqu’à ce nous soyons allés de (P,0) à (0,Q). Une fois cela fait, l’arbre contiendra tout chemin possible.
  - Le nombre de façons d’aller de (P,1) à un nœud (I,J) dans cet arbre est le nombre de façons d’atteindre (I-1,J), et ensuite de descendre en bas à droite à (I,J), plus le nombre de façons d’atteindre (I,J-1) et de descendre en bas à gauche à (I,J). Dit autrement, c’est le nombre dans le Triangle de Pascal.
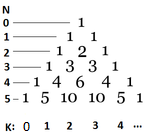
  - Chaque nombre dans le Triangle de Pascal égale la somme des deux nombres là-dessus. Les nombres dans la colonne à gauche comptent les rangées du plateau, commençant par 0 (le plateau vide). Les nombres sous le triangle représentent la position à partir de la gauche, commençant aussi de 0. Le nombre dans la Nème rangée dans la position K est égal à \({N \choose K} = \frac{N!}{(N-K)!K!}\).
  - On veut trouver le nombre f(P,Q) qui égale le nombre de façons d’aller de (P,0) à (0,Q). Pour le faire, il faut se déplacer du coin supérieur gauche P fois en bas à droite et Q fois en bas à gauche. Si on consulte l’arbre déjà défini, ceci est équivaut à aller de (0,0) à (P,Q) en se déplacant qu’à droite et à gauche dans l’arbre.
  - Cependant, cela nous oblige de faire P+Q pas, donc nous sommes dans la rangée P+Q de l’arbre. Puisque nous savons que nous nous sommes déplacés Q fois à droite, le nombre dans le Triangle de Pascale pour cette position est \({P+Q \choose Q} = \frac{(P+Q)!}{P!Q!}\).
- Démonstration d’une Formule Explicite par Induction
  - Ici nous allons montrer que les deux formules suivantes sont égales. \[f(P,Q) = \begin{cases}1 & for & P=0 \\1 & for & Q=0 \\f(P,Q-1) + f(P-1,Q) & for & \text{P>0 and Q>0}\end{cases} = \Bigg\{{P+Q \choose Q} = \frac{(P+Q)!}{P!Q!}\]
  - Initialisation : On sait déjà que f(0,0) = 1 par la definition de la formule. Si on entre P=0 et Q=0 dans la formule, elle nous rend \(\frac{(0+0)!}{0!0!} = \frac{0!}{1} = 1\). Ainsi démontre-t-on que les formules de base sont égales, ce qui suffit pour l’initialisation de la démonstration par recurrence.
  - Hypothèse : Disons que les deux formules sont égales pour toutes les valeurs de P,Q où P+Q=N.
  - Hérédité : On se sert de l’hypothèse pour démontrer l’équivalence pour toutes les valeurs de P,Q où P+Q=N+1. Pour n’importe quelles valeurs de P,Q où P+Q=N+q, nous avons trois cas:
  - Cas 1 :
  - Cas 2 :
  - Cas 3 : \(P,Q > 0\) \[ \begin{align} f(P,Q) &= f(P,Q-1) + f(P-1,Q)\qquad\qquad (+)\\ &= \frac{(P+Q-1)!}{P!(Q-1)!} + \frac{(P-1+Q)!}{(P-1)!Q!}\\ &= \frac{(P+Q-1)!Q}{P!(Q-1)!Q} + \frac{(P-1+Q)!P}{(P-1)!PQ!}\\ &= \frac{(P+Q-1)!}{P!Q!} (Q+P)\\ &= \frac{(P+Q)!}{P!Q!} \end{align} \]
  - (+): Si P + Q = N + 1, alors P + Q – 1 = N, ç.-à-d. par l’hypothèse d'induction.
    f(P,Q-1) = \(\frac{(P+(Q-1))!}{(P!(Q-1)!)}\), et similairement pour f(P-1, Q)
  - Ainsi montre-t-on que les deux formules calculant f(P,Q) sont équivalentes.
  - Fin de Démonstration. ∎

Combien de positions différentes ont un nombre P de rangées et un nombre Q de colonnes ?
- On peut utiliser tout simplement la même formule que celle qui trouve le nombre total de positions possibles dans un rectangle qui a P-1 rangées et Q-1 colonnes, c’est-à-dire f(P-1, Q-1).

Est-ce qu’il y a plus de positions gagnantes ou perdantes?

# de Tuiles	# de positions	# de positions perdantes	% de positions perdantes
20	627	42	6.69
30	5604	220	3.92
40	37338	1022	2.73
50	204226	4976	2.43
60	966467	20106	2.08
70	4087968	76688	1.87
80	15796476	270142	1.71
90	56634173	897964	1.58

Une Hypothèse par Caribou

On a déjà démontré que chaque position est soit perdante soit gagnante. La démonstration a rendu une méthode pour déterminer, étape par étape, si une position est gagnante ou perdante. Ce qui était particulier, c’était le fait que cette méthode ne nécessitait pas de recherche (pas besoin de faire des coups d’essai). Ça nous a rappelé la ‘Crible d’Ératosthène’ qui sert à déterminer les nombres premiers jusqu’à une certaine valeur.

Vous pouvez découvrir la Crible d’Ératosthène, sur l’internet par exemple
- Pour trouver tous les nombres premiers jusqu’à la valeur N², où N est un nombre entier, il faut faire la suite :
- - A: Commencer avec le nombre premier p=2.
  - B: B: Raturer tous les multiples de p jusqu’à N².
  - C: Trouver le prochain nombre >p qu’on n’a pas encore raturé. Si le nombre > N, l’algorithme s’arrête. Sinon, on appelle ce nombre p et on continue avec l’étape B.
- Tous les nombres jusqu’à N² qui ne sont pas raturés sont les nombres premiers <N². On peut trouver une simulation de cet algorithme sur https://en.wikipedia.org/wiki/Sieve_of_Eratosthenes

Cette analogie nous a encouragés à penser à d’autres similitudes partagées par les nombres premiers et les positions perdantes. Elle nous a menés à une hypothèse pour les positions perdantes qui ressemble au ‘Théorème des Nombres Premiers’. Les détails suivront.

Table: Analogies entre les positions perdantes dans Chomp et les nombres premiers:

Nombres	Chomp
Il y a un nombre infini de nombres entiers.	Il y a un nombre infini de positions Chomp.
Il y a des nombres premiers et des nombres composés.	Il y a des positions perdantes et des positions gagnantes.
Il y a un nombre infini de nombres premiers.	Il y a un nombre infini de positions perdantes.
Un nombre composé est le produit d’un nombre premier et un nombre.	Une position gagnante est la somme d’une position perdante et une position (car ce qui est supprimé par un coup a la forme d’un escalier, et est donc une position).
Une fois un nombre premier reconnu, on connaît instantanément un nombre infini de nombres composés (les multiples dudit nombre premier).	Une fois une position perdante reconnue, on connaît instantanément un nombre infini de positions gagnantes (toutes les positions résultant de remplir les rectangles aux coins, y compris ceux qui ont une longueur et une largeur infinie.
Un grand nombre est beaucoup plus susceptible d'être divisible par un petit nombre premier que par un grand nombre premier.	Une grande place est beaucoup plus susceptible d'être réductible à une petite position perdante que d' une grande position perdante.
Afin de déterminer si un nombre N est un nombre premier de façon efficace, il est utile de connaître tous les nombres premiers P jusqu’à la racine carrée de N. On peut alors vérifier si on peut réduire N à P par division (ç.-à-d. en divisant N / P).	Afin de déterminer si ue position P est perdante, il est nécessaire de connaître toutes les positions perdantes L qui sont contenues dans P. On peut alors vérifier de façon efficace si on peut réduire P à L en un coup.
La ‘Crible d’Ératosthène’ est une façon efficace de déterminer tous les nombres premiers jusqu’à un nombre N, mais aussi pour vérifier si un nombre donné est un nombre premier. On a décrit l’algorithme en haut.	Comme dans la ‘Crible d’Ératosthène’, on commence par la position perdante {1}, et on rature toutes les positions gagnantes qui se réduisent à cette position en un seul coup. On analyse ensuite toutes les positions avec une tuile de plus. Toutes les positions qui ne sont pas raturées sont perdantes.
L’aspect le moins efficace de cette ‘crible’ consiste de devoir toujours raturer les nombres composés.	L’aspect le moins efficace de cette ‘crible’ consiste de devoir toujours raturer les positions gagnantes.
La densité des nombres premiers diminue plus les valeurs montent. Ç.-à-d. la proportion (nombre de nombres premiers jusqu’à un nombre enter N) / N diminue au fur et à mesure que N monte.	La densité des positions perdantes diminue plus le plateau et grand. Ç.-à-d. la propotion (nombre de positions perdantes jusqu’à un nombre N de tuiles) / (nombre de toutes les positions avec N tuiles) diminue au fur et à mesure que N monte. (Défi: Quelle est la formule qui calcule la dépendance de cette proportion sur N et quel est le rapport avec la formule qui calcule la densité des nombres premiers?)
Théorème des Nombres Premiers : (nombre de nombres premiers < N) / (N / log(N)) &rarr 1 quand N → l’infini	Hypothèse analogique: (nombre de positions perdantes comportant N tuiles) / ((nombre de positions comportant N tuiles) / log(nombre de positions comportant N tuiles)) → 0,286... quand N → l’infini.

Table: Les Différences entre les positions perdantes dans Chomp et les nombres premiers.

Nombres	Chomp
L’ensemble des nombres entiers est un ensemble bien ordonné ; ç.-à-d. à choisir entre deux nombres donnés, on sait lequel est plus grand.	L’ensemble de toutes les positions Chomp est partiellement ordonné. Une position peut être contenue dans d’autres positions, mais pas nécessairement.
L’opération qui réduit un nombre à un de ses facteurs premiers est la division.	L’opération qui réduit une position à une position perdante est une soustraction de tuiles.
On peut visualiser un nombre comme un segment de droite sur une droite graduée d’une dimension.	Une position se définit par une liste de nombres ordonnés par valeur, elle est donc un object à deux dimensions.

Questions Ouvertes:

Est ce que cette hypothèse, (nombre de positions perdantes comportant N tuiles) / ((nombre de positions comportant N tuiles) / log(nombre de positions comportant N tuiles)) → 0,286... quand N → l’infini, est vraie?

Est-ce que vous pouvez la démontrer? (Nous, pas encore! :-) )

Le jeu de Chomp joué ci-dessus est une version à deux dimensions, le plateau du jeu a une longueur et une largeur.

Pouvez-vous en imaginer une Version 3D?
- La façon la plus simple de concevoir une nouvelle dimension sera d’ajouter une troisième dimension au plateau. En plus d’une longueur et d’une largeur, le nouveau plateau aurait aussi une hauteur. Si on pouvait jouer avec des petits cubes comme des dés, on pourrait jouer à ce jeu 3D comme on le montre ci-dessous.
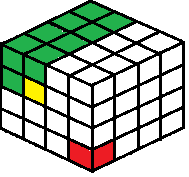
- Quand on joue un coup, on enleverait le cube sélectionné ainsi que tous les cubes supérieurs gauches et en haut du cube sélectionné. Un coup possible est illustré en jaune dans l’image, qui enlève aussi tous les cubes verts. Le joueur qui sélectionne la dernière tuile, ici en rouge, perd la partie.
- Pour rendre le jeu plus facile avec de vrais cubes, on pourrait pousser tous les cubes dans un coin, comme celui d’une boîte à chaussures, pour que la tuile rouge soit dans le coin qui n’est accessible que quand tous les autres cubes sont déjà enlevés. Il n’est pas nécessaire d’utiliser une boîte mais ce serait utile pour stabiliser la structure de sorte qu’on puisse enlever un cube sans le risque de faire tomber la structure entière.

Et Si On Ajoutait Encore Plus de Dimensions?
- On a déjà vu qu’il n’est pas trop difficile d’ajouter une nouvelle dimension au jeu Chomp. Si on voulait jouer un jeu Chomp avec au-délà de 3 dimensions, on pourrait continuer à ajouter des dimensions au plateau. Cependant, au-délà de 3D, il n’est plus possible de simuler le plateau de Chomp avec des cubes. Par contre, il existe une façon de simuler un tel jeu avec un crayon et du papier, et cette méthode permet de jouer le jeu avec tout nombre voulu de dimensions, pas seulement en 2D ou en 3D.
- Pour commencer on joue une partie de Chomp en 2D sur papier. Une façon de simuler le jeu est de sélectionner un nombre qui n’a que 2 facteurs premiers. Par exemple, 72=2³ x 3². On écrit ensuite tous les facteurs de ce nombre sous la forme d’un rectangle, comme ci-dessous.
- 72 36 18 9
  24 12 6 3
  8 4 2 1
- Tout nombre à droite et plus petit par un facteur de 2, et tout nombre en bas est plus petit par un facteur de 3. Pour jouer un coup sur ce plateau, on sélectionne un nombre. On enlève ensuite ce nombre ainsi que tous ses facteurs. Le joueur qui sélectionne le nombre 72 perd la partie.
- Pour commencer avec un rectangle plus grand, on pourrait trouver un plus grand nombre avec la formule 2^P x 3^Q. Plus on met de grands nombres à la place de P et Q, plus le plateau de Chomp en 2D est grand.
- Comment Généraliser cette Simulation aux Autres Dimensions?
  - Pour faire étendre cette version au crayon et au papier de Chomp de 2D à 3D, il faut étendre la formule utilisée pour trouver le nombre de départ. Au lieu de sélectionner un nombre qui n’a que 2 facteurs premiers, on trouverait un nombre qui a 3 facteurs premiers, dont 2^P x 3^Q x 5^R. Ensuite on utiliserait les mêmes méthodes qu’avant pour simuler le jeu en 3 dimensions. Passer aux dimensions encore plus hautes nécessite ajouter encore de nombres premiers aux formules dépendamment du nombre souhaité de dimensions.