Chomp ©

Ein Feld ist der Schnittpunkt einer Zeile und einer Spalte, die mit (Zeile, Spalte) beschriftet sind.
Eine Kachel ist das Bild auf einigen Feldern.
Eine Position besteht aus allen Feldern mit Kacheln.

Beginnen wir mit einfachen Problemen, d.h. kleinen Positionen. Um sie zu erstellen, klicken wir auf 'Computer: Aus'. Wenn wir dann auf (2,1) klicken, bleibt nur noch eine Reihe von Kacheln übrig.

Was kann der nächste Spieler, also der Gegner, tun?
- Mit einem Klick auf (1,2) bleibt nur noch das Plättchen auf (1,1) übrig, so dass Sie verloren haben.

Klicken wir dann auf "Neues Spiel" und auf (3,1) und (2,2), um ein Plättchen in Reihe 2 und die gesamte Reihe 1 zu haben.

Was kann der nächste Spieler tun?
- Mit einem Klick auf (1,3) bleiben nur noch drei Kacheln übrig. Siehst du, dass du keine Chance hast?

Klicken Sie auf "Neues Spiel" und klicken Sie auf (3,1) und (2,3).

Was kann der nächste Spieler tun?
- Dein Gegner kann auf (1,4) klicken. Siehst du, dass du keine Chance hast?

Kannst du zusammenfassen, auf welchen Positionen du mit Plättchen in nur 2 Reihen keine Chance hast, das Spiel zu gewinnen?
- Wenn die oberste Reihe ein Plättchen mehr hat als die 2. Reihe, dann kann dein Gegner immer einen Zug machen, so dass die obere Reihe ein Plättchen mehr hat als die 2. Reihe. Egal, was du tust, irgendwann musst du das Plättchen (1,1) wählen und das Spiel verlieren.

Wenn auf eine Kachel geklickt wird, werden auch alle Kacheln darunter und rechts davon entfernt. Diese Regel weist eine Symmetrie auf. d.h. das ganze Spiel hat folgende Symmetrie: Wenn wir Zeilen und Spalten vertauschen, bleibt die Regel gleich: Alle Plättchen rechts werden zu allen Plättchen darunter und alle Plättchen darunter zu allen Plättchen rechts vom entfernten Plättchen. Mit anderen Worten, wenn wir eine Position entlang der Linie durch (1,1) und (2,2) spiegeln, dann kann die neue Position anders aussehen, aber sie hat den gleichen Status. Der Gewinnzug ist auch derselbe Zug, nur ebenfalls gespiegelt.

Die Stellung mit 3 Plättchen in der ersten Reihe und 2 Plättchen in der zweiten Reihe ist, wie wir wissen, hoffnungslos. Welche Kacheln haben die gespiegelten Positionen?
- Nach der Spiegelung hat es 3 Kacheln in der linken Spalte und 2 Kacheln in der 2. Spalte.

Wir kennen alle hoffnungslosen Stellungen, die nur in den ersten beiden Reihen Kacheln haben. Was sagt uns die Symmetrie über alle hoffnungslosen Stellungen mit Kacheln nur in den ersten beiden Spalten?
- Hoffnungslose Positionen mit Kacheln in den ersten beiden Spalten sind solche, bei denen die erste Spalte ein Plättchen mehr hat als die zweite Spalte.

Hier ist eine weitere Position ohne Chance: Klicken Sie auf "Neues Spiel" und auf (4,1), (2,2) und (1,4).

Wenn der Gegner in dieser Stellung einen Zug macht, was ist deine Antwort?
- Sie müssen sicherstellen, dass nach dem Verschieben die oberste Zeile und die erste Spalte wieder die gleiche Länge haben. Durch die Wiederholung dieses Musters muss der Gegner schließlich das Plättchen (1,1) nehmen und verlieren.

Wenn also die erste Zeile und die erste Spalte die gleiche Anzahl von Kacheln haben und es keine anderen Kacheln gibt, dann ist die Position hoffnungslos. Welche Positionen können in eine solche Position gewechselt werden?
- Wenn eine Stellung die gleiche Anzahl von Reihen und Spalten hat, egal wie viele Plättchen es anderswo gibt: Ein Zug weiter (2,2) lässt nur die erste Reihe und die erste Spalte gleich lang und lässt dem Gegner keine Chance. Wenn also eine Position die gleiche Anzahl von Plättchen in der obersten Reihe wie in der linken Spalte hat, dann spielst du bei (2,2) und gewinnst das Spiel.

Um Chomp gut zu spielen, muss man wissen, wie man Positionen gewinnt und verliert. Eine Gewinnstellung ist eine, in der man einen Gewinn erzwingen kann, wenn man optimal spielt, unabhängig davon, was die andere Seite tut. Eine Verliererstellung ist eine Stellung, in der man keine Chance hat, wenn die andere Seite optimal spielt. Die folgenden Punkte sind das, was man in der Mathematik eine Definition nennt. In Chomp werden Verlust- und Gewinnpositionen durch diese 3 Punkte definiert:
1. Wenn nur noch ein Plättchen übrig ist (in der oberen linken Ecke), dann ist dies eine Verlustposition.
2. Eine Stellung ist eine Gewinnstellung, wenn es einen Zug gibt , der zu einer Verluststellung für den Gegner führt.
3. Eine Stellung ist eine Verluststellung, wenn jeder Zug zu einer Gewinnstellung für den Gegner führt.
Auf den ersten Blick mögen die oben genannten Punkte nutzlos erscheinen, da Gewinnpositionen durch Verlustpositionen erklärt werden und Verlustpositionen durch Gewinnpositionen erklärt werden. Nichtsdestotrotz basiert die Definition auf dem Ausführen von Zügen, und jede Abfolge von Zügen führt schließlich zu der einzelnen Plättchenposition, die gemäß Punkt 1 eine Verlustposition ist.

Ist es möglich, dass es Positionen gibt, in denen keine der beiden Seiten einen Sieg erzwingen kann? (schwierig)
- Wir werden ein kleines Theorem formulieren und beweisen. Der Beweis wird uns den Weg zeigen, wie wir die perfekte Spielstärke erreichen können. Der Beweis ist ein Beweis durch Induktion, bei dem man zeigt, dass die Aussage, die wir beweisen wollen, für eine Kachel wahr ist, und dann zeigt, dass, wenn sie für eine beliebige Anzahl von N Kacheln wahr ist, sie auch für eine weitere Kachel wahr sein muss, d.h. N+1 Kacheln. Da diese Aussage für N=1-Kacheln gilt, muss sie auch für N+1=1+1=2-Kacheln wahr sein. Da es aber für N=2 gilt, muss es auch für N+1=2+1=3 Kacheln wahr sein, und so weiter; d.h. für beliebig viele Kacheln.
- Lemma (kleiner Satz): Jede Position ist entweder eine Gewinn- oder eine Verlustposition.
- Nachweis durch Induktion:
- Induktionsbasis: Wenn die Stellung nur ein Plättchen hat, dann ist dieses Plättchen in der oberen linken Ecke und dann ist die Stellung eine Verlustposition gemäß der Chomp-Regel (die zeigt, dass das Lemma wahr ist, wenn nur N=1 Plättchen vorhanden ist).
- Induktionsvoraussetzung: Wir gehen davon aus, dass das Lemma für alle Positionen mit bis zu N Plättchen gilt, d.h. Positionen mit 1,2,..., N Plättchen sind entweder Gewinn- oder Verlustpositionen.
- Induktionsschritt: Wir wollen nun zeigen, dass auch dann alle Positionen mit N+1-Plättchen entweder Verlierer- oder Gewinnpositionen sein müssen.
- Im folgenden P ist eine beliebige Position mit N+1 Kacheln. Wenn P um einen Zug reduziert wird, muss die neue Stellung ≤N Plättchen haben, also ist es eine Verlust- oder Gewinnstellung gemäß der Induktionshypothese. Wenn P in einem Zug auf eine Verlustposition reduziert werden kann, dann ist P eine Gewinnstellung. Wenn nicht, dann kann P in einem Zug nur auf eine Gewinnstellung reduziert werden. Aber wenn eine Stellung im Zug nur auf eine Gewinnstellung reduziert werden kann, dann muss P eine Verlustposition sein. Dies beweist, dass P (mit N+1 Plättchen) entweder eine Gewinn- oder eine Verliererposition ist. Dies zeigt, dass alle Positionen (mit N+2,N+3,... Plättchen) sind entweder Gewinn- oder Verlustpositionen.
  
  Ende des Beweises ∎
- Ergänzende Bemerkung: Der Induktionsschritt bietet eine Methode, um für alle Positionen (bis zu einer gewissen Größe) zu entscheiden, ob es sich um Gewinn- oder Verlustpositionen handelt. Sie wird wie folgt definiert:
  
  Man beginnt mit N=1 und bezeichnet diese Position als Verlustposition. Man bestimmt dann den Status aller Positionen mit 2 Plättchen, dann mit 3 Plättchen usw., wobei man jedes Mal das Wissen um den Status der kleineren Positionen nutzt und die neu gefundene Verlustposition zur Liste der bekannten Verlustpositionen hinzufügt.
- Dies ist ein sehr effizienter Weg, um alle Gewinn- und Verlustpositionen bis zu einer gewissen Größe zu finden. Wenn die Zahlen größer werden, wäre ein Computerprogramm hilfreich. Notwendige Zutaten sind wie folgt:
  - Eine Prozedur, die effizient alle Positionen von N Kacheln erstellen kann, indem alle Positionen von weniger als N Kacheln bekannt sind
  - Ein Verfahren, mit dem effizient geprüft werden kann, ob eine Position auf eine andere Position reduziert werden kann oder nicht.
  Wir überlassen es Ihnen, mehr darüber nachzudenken und vielleicht ein solches Computerprogramm zu schreiben.

Wie viele Verlust- und Gewinnpositionen haben genau 2 Plättchen?
- Es gibt nur zwei mögliche Positionen, die genau 2 Kacheln haben, 2 Kacheln in der obersten Reihe oder zwei Kacheln entlang der linken Spalte. Beide Positionen sind Gewinnpositionen.

Wie viele Verlust- und Gewinnpositionen haben genau 3 Plättchen?
- Es gibt insgesamt 3 mögliche Positionen, die genau 3 Kacheln haben. Sie bestehen aus 2 Gewinnpositionen und 1 Verlustposition. Können Sie herausfinden, welche Positionen das sind?

Wie viele Verlust- und Gewinnpositionen haben genau 4 Plättchen?
- Es gibt 5 mögliche Positionen, die genau 4 Kacheln haben. Alle diese Positionen sind Gewinnpositionen.

Wie viele Verlust- und Gewinnpositionen haben genau 5 Plättchen?
- Es gibt insgesamt 7 mögliche Positionen, die genau 5 Kacheln haben. Von diesen Positionen sind 3 Verlustpositionen und 4 Gewinnpositionen. Können Sie herausfinden, welche das sind?

Gewinnen oder verlieren rechteckige Positionen?
- Das folgende Lemma beantwortet diese Frage. Der Beweis ist ein Existenzbeweis. Es wird nur die Existenz eines Gewinnzugs beweisen, ohne zu zeigen, was der Zug ist. Nichtsdestotrotz ist es für Ihr Spiel nützlich, das Lemma zu kennen, wie unten erläutert.
- Lemma: Alle rechteckigen Positionen mit Ausnahme der 1-Kachel-Position sind Gewinnpositionen.
- Beweis: Um zu zeigen, dass dies wahr ist, müssen wir zwei mögliche Fälle betrachten:
  1. Das Entfernen der Kachel in der unteren rechten Ecke des Spielbretts ist ein gewinnbringender Schachzug.
  2. Das Entfernen der Kachel in der unteren rechten Ecke ist kein Gewinn.
- Wenn Fall 1 wahr ist, dann bedeutet das, dass das Rechteck eine Gewinnposition ist, und das unterstützt das Lemma.
- Wenn Fall 1 nicht wahr ist, müssen wir Fall 2 betrachten. Nach dem Beweis, den wir zuvor gemacht haben, muss die Stellung, die sich aus dem Entfernen des Plättchens in der unteren rechten Ecke ergibt, dann eine Gewinnstellung sein, was bedeutet, dass es einen Gewinnzug geben muss. Da jedoch jeder Zug in einem Rechteck das Plättchen in der unteren rechten Ecke entfernt, ist die Verluststellung, die sich aus dem 2. Zug (dem Gewinnzug) ergibt, die gleiche, unabhängig davon, ob der Gewinnzug nach dem Eckzug oder anstelle des Eckzugs gespielt wird. Das bedeutet, dass der Gewinnzug sofort hätte gespielt werden können, was beweist, dass ein Gewinnzug für die rechteckige Stellung existiert.
- Ende des Beweises ∎
- Ergänzende Anmerkungen: Obwohl das Lemma uns nicht sagt, was der Gewinnzug ist, ist es bereits hilfreich zu wissen, dass rechteckige Stellungen Gewinnstellungen sind. Man sollte daher keinen Zug machen, der eine rechteckige Position erzeugt (außer der 1x1-Position).

Können Sie für ein beliebiges quadratisches Brett bestimmen, was der Gewinnzug ist?
- Bei allen Feldern der Größe >1 ist der einzige Gewinnzug auf (2,2).

Für welche Stellungen, die einem Feld ähneln, ist derselbe Zug ein Gewinnzug?
- Der Zug (2,2) ist auch ein Gewinnzug für jede Position, in der die 1. Reihe und die 1. Spalte gleich lang sind.

Kann eine Stellung mehr als einen Gewinnzug haben?
- Ja, eine Position kann mehr als einen Gewinnzug haben. Betrachten Sie die folgende Position:
  
  ###
  ##
  #
  
  Diese Brettstellung hat 3 verschiedene Gewinnzüge, die gemacht werden können. Können Sie feststellen, welche das sind?

Die allgemeine Strategie, um bei Chomp zu gewinnen, besteht darin, Verlustpositionen für Ihren Gegner zu schaffen, damit er keine Chance hat. Wir wollen auch vermeiden, Gewinnstellungen zu schaffen, die der Gegner wieder in Verliererstellungen für uns verwandeln kann.

Der Schlüssel zum Sieg liegt darin, so viele Verlustpositionen wie möglich zu kennen und zu erkennen, wie man eine bildet, bevor es der Gegner tut. Betrachten wir das folgende mögliche Spielbrett, bei dem es sich um eine bekannte Verlustposition handelt:

#######
###
###
#
#
Abbildung 1

Was sind all die Positionen, die in einem Zug in diese Verlustposition verwandelt werden können?

Die obige Verlustposition kann aus jeder Bewegung resultieren, die unten mit einem + gekennzeichnet ist:

#######+
###
###
#
#

#######
###+
###
#
#

#######
###
###
#+
#

#######
###
###
#
#
+

Abbildung 2

Diese Bewegungen befinden sich alle in den ausgeschnittenen Ecken. Eine solche +-Bewegung schneidet auch Kacheln aus, die in den folgenden Bildern mit ? erscheinen können:

#######+?
###
###
#
#

#######
###+???
###????
#
#

#######
###
###
#+?
#??

#######
###
###
#
#
+
?

Abbildung 3

Die Kacheln + sind notwendig, und das ? Kacheln sind optional. In der linken Gewinnposition kann die obere Reihe beliebig nach rechts mit mehr '?' verlängert werden, und in der rechten Gewinnposition kann die erste Spalte beliebig nach unten mit mehr '?' verlängert werden. Alle diese Positionen sind auch Gewinnpositionen. Wenn wir in einer solchen Stellung einen Zug machen, nehmen wir ein +-Plättchen und damit alle ? Verbundene Kacheln werden ebenfalls entfernt, was zu der Ausgangsposition führt.

Gibt es mehr Gewinn- oder mehr Verlustpositionen?
- Für jede Verlustposition gibt es unendlich viele Positionen, die durch einen einzigen Zug in diese Verlustposition verwandelt werden können. All diese unendlich vielen Positionen sind daher Gewinnpositionen.
- Daher gibt es viel mehr Gewinnpositionen als Verlustpositionen. Daher ist es am effektivsten, sich so viele Verlustpositionen wie möglich zu merken, alle anderen Positionen sind Gewinnpositionen.

Erstellen Sie eine Liste der Verlustpositionen, die Sie kennen, und schreiben Sie für jede Position alle entsprechenden Gewinnpositionen auf und wie Sie sie erkennen können

Das folgende Beispiel zeigt, was wir meinen:

Wie bereits gezeigt, handelt es sich bei einer Position, die nur 2 Reihen hat und die oberste Reihe eine Kachel mehr als die zweite Reihe hat, um eine Verlustposition, wie unten gezeigt:

#####
####
Ausgehend von dieser bekannten Verlustposition können wir feststellen, dass die entsprechenden Gewinnpositionen sind:

#####+?
####

#####
####+

#####
####
+???
????

In der linken Position kann es eine beliebige Anzahl von ? Rechts neben der obersten Zeile und an der richtigen Position kann sich eine beliebige Anzahl von Zeilen von ? unter. Wir können in Worten zusammenfassen, wie man diese Gewinnstellungen erkennt (die Sie sich für Ihr Spiel merken sollten):

- Eine Position ist eine Gewinnposition, die sich auf
  #####
  ####
- - Wenn entweder die Position nur zwei Reihen hat und die erste Reihe nicht genau eine Kachel länger ist als die zweite Reihe, oder
- - Wenn die Position mehr als zwei Reihen hat und die erste Reihe genau eine Kachel länger ist als die zweite Reihe.
Aber es gibt noch mehr zu bedenken. Wir wollen in solchen Gewinnstellungen nicht nur richtig spielen, sondern auch vermeiden, einen Zug zu machen, der solche Gewinnstellungen schafft. Das bedeutet, dass wir keinen Zug machen sollten, bei dem nur noch zwei Reihen übrig sind oder bei dem die zweite Reihe genau ein Plättchen weniger hat als die erste Reihe.

Zusammenfassend lässt sich sagen, dass wir Verlustpositionen schaffen wollen, aber wir wollen auch vermeiden, Positionen zu schaffen, die nur eine Bewegung von einer Verlustposition entfernt sind.

Eine weitere Sache, die zu beachten ist: Aufgrund der bereits erwähnten Spiegelsymmetrie können alle obigen Kommentare wiederholt werden, indem einfach das Wort "Zeile" durch das Wort "Spalte" ersetzt wird.

Es liegt an Ihnen, weitere Verlustpositionen und die entsprechenden Gewinnpositionen zu sammeln, die nur einen Zug entfernt sind.

Was ist, wenn Sie auf verlorenem Posten spielen müssen?
- Wenn Sie feststellen, dass Sie in einer Verlustposition einen Zug machen müssen, dann haben Sie theoretisch keine Chance. Alles, was Sie tun können, ist zu hoffen, dass Ihr Gegner nicht alle Gewinnzüge für die Stellungen kennt, die Sie mit Ihrem nächsten Zug erstellen können. Was Sie tun können, ist, nur eine einzelne Kachel aus einer Ecke zu entfernen. Dadurch erhält Ihr Gegner eine resultierende Stellung von maximaler Größe und es wird für Ihren Gegner schwieriger, den entsprechenden Gewinnzug zu kennen.

Wie lernt man das Verlieren von Positionen auf eigene Faust?
- Man müsste eine sogenannte vollständige Baumsuche durchführen. Der erste Spieler beginnt damit, einen Zug zu erraten, dann errät der zweite Spieler einen Zug und so weiter, bis ein Spieler, z.B. Spieler A, gewinnt. Dann darf Spieler B den letzten Zug ändern und als nächstes ist Spieler A an der Reihe. Wenn in einer Stellung dem Spieler, der als nächstes spielt, z.B. B, die Züge ausgehen, weil alle Züge zu einer Niederlage führen, dann ist dies eine Verluststellung, und Spieler B kann den letzten Zug ändern, der vor dem Erreichen dieser Verluststellung gemacht wurde.
- Diese "Baumsuche" wird so lange fortgesetzt, bis klar ist, ob die Startposition eine Verluststellung ist oder welcher Zug von Spieler 1 sie in eine Verluststellung verwandelt.
- Dies kann ein sehr langwieriger Prozess sein, wenn man versucht, dies auf einem anfänglichen Brett mit vielen Plättchen zu tun. Je mehr Verlustpositionen wir jedoch kennen, desto kürzer sind die Zugfolgen, bevor eine solche Position erreicht wird, und somit ist die gesamte Suche viel schneller. Wenn wir wüssten, dass alle Verlustpositionen enthalten sind, dann würde entweder die Startposition als Verlustposition erkannt werden, oder es wäre nur ein Zug notwendig, um sie auf eine Verlustposition zu reduzieren.

Wie lernt man, Positionen mit dem Computer zu verlieren?
- Im Schwierigkeitsgrad "Sehr schwer" und Stellungen, die nicht größer als 8 x 15 sind, spielt der Computer perfekt, so dass jede Stellung, die sich aus einem Computerzug ergibt, eine verlorene Position ist! Man sollte mit sehr kleinen Brettern beginnen und im Level "Sehr schwer" gegen den Computer spielen und alle Stellungen lernen, die der Computer generiert. Überlegen Sie sich für jede dieser Stellungen, wie jeder Ihrer Züge vom Computer beantwortet werden würde, um ihn wieder in eine kleinere Verlustposition zu verwandeln. Für jede Verlustposition ist auch die gespiegelte Position (Zeilen <--> , Spalten) eine Verlustposition.
- Was ist ein optimaler erster Zug?
  - Im Wettbewerb ist die Startposition ein Rechteck aus Bonbons. Wie bereits bewiesen, ist ein Rechteck eine Gewinnstellung, aber was ist der erste Zug, der es in eine Verluststellung für den Gegner verwandelt? Wir haben vorhin gelernt, dass der optimale Zug für ein Quadrat die Kachel (2,2) ist, aber was ist, wenn das Rechteck kein Quadrat ist?
  - Wechseln Sie einfach in den Schwierigkeitsgrad "sehr schwer" und lassen Sie den Computer den ersten Schritt machen. Solange das Rechteck nicht größer als 8x15 ist, spielt der Computer optimal und zeigt den perfekten ersten Zug. Probieren Sie verschiedene Rechteckgrößen aus und merken Sie sich den optimalen ersten Zug, da das Computerspiel an den Wettkampftagen :) nicht verfügbar ist.
- Bald wirst du im leichten und mittleren Schwierigkeitsgrad unschlagbar sein.

Gibt es unendlich viele Familien von Verlustpositionen?
- Wir haben diese beiden Familien von Verliererpositionen bereits kennengelernt. N ist eine beliebige positive ganze Zahl.
- Hier sind noch mehr:

Der in das Spiel eingebaute Computerspieler verwendet verschiedene Techniken für verschiedene Spielniveaus.

- Leicht- Führt in jeder Runde zufällige Züge aus. Wenn eine einfache Gewinnposition erkannt wird, bewegt er sich dorthin.
- Mittel- Bewegt sich immer noch zufällig, hat aber ein größeres Wissen über Gewinn- und Verlustpositionen. Vermeidet Züge, die dem Gegner Zugang zu einem einfachen Gewinnzug geben.
- Schwer- Verfügt über ein noch größeres Wissen über Gewinnpositionen. Sucht aktiv auf dem Brett nach Zügen, die den Gegner dazu zwingen können, selbst einen verlorenen Zug zu machen.
- Sehr schwer - Macht immer den optimalen Zug für jede Position, die in ein Rechteck der Größe 8x15 passt.
Je höher der Schwierigkeitsgrad, desto schwieriger wird es, den Computer in eine verlorene Position zu zwingen. Jedes Level kennt viel mehr Gewinn- und Verlustpositionen als das vorherige Level, und je schwieriger der Schwierigkeitsgrad, desto mehr Gewinn- und Verlustpositionen müssen Sie kennen, um zu versuchen, den Computer in eine Verlustposition zu zwingen.

Die folgenden Bemerkungen werden nicht dazu beitragen, in Chomp stärker zu werden, aber sie werden einige interessante Tatsachen liefern und uns eine weitere Gelegenheit geben, Beweise durch Induktion zu üben.

Wie viele verschiedene Positionen, einschließlich der leeren Tafel, passen in ein Rechteck mit P-Zeilen und Q-Spalten?
- Wenn wir das leere Rechteck einbeziehen, können wir die Gesamtzahl der möglichen Positionen mit der folgenden Formel berechnen: \[\frac{(P+Q)!}{P!Q!}\]Können Sie diese Zahl für ein kleines P und Q berechnen und überprüfen, ob sie korrekt ist?
- Erste Herleitung einer rekursiven Formel
  - Sei f(P,Q) die Anzahl der Positionen in einem Rechteck der Größe PxQ. Eine wichtige Beobachtung ist, dass alle Positionen die Form einer Treppe haben, wobei jede Reihe höchstens so viele Kacheln hat wie die Reihe darüber, aber nicht mehr.
  - Beginnen wir zunächst mit einer Möglichkeit, wie wir all diese Treppen darstellen können. Eine Möglichkeit, eine Treppe einfach zu erstellen, besteht darin, in der unteren linken Ecke des Bretts zu beginnen und sich entweder nach rechts oder nach oben zu bewegen. Man kann diese Züge nach rechts und nach oben so lange machen, bis sie in der oberen rechten Ecke des Bretts ankommen. Wir bezeichnen dies als einen Weg , den wir genommen haben, um von (P,0) nach (0,Q) zu gelangen.
  - Die Anzahl der Positionen ist die gleiche wie die Anzahl der Pfade von (P,0) bis (0,Q), solange man sich nur nach oben oder nach rechts bewegen darf. Die Anzahl f(P,Q+1) der Pfade, die von (P,0) nach (0,Q+1) gelangen sollen, ist die Anzahl f(P,Q) der Pfade, die von (P,0) nach (0,Q) und dann nach (0,Q+1) + die Anzahl f(P-1,Q) der Pfade, die von (P,0) nach (1,Q) und dann nach (1, Q+1) und (0,Q+1) usw. Die entsprechende Formel lautet wie folgt:\[f(P,Q+1) = f(P,Q) + f(P-1,Q) + f(P-2,Q) + \ldots + f(1,Q) + f(0,Q)\]
  - Wir nehmen nun diese Formel und ersetzen P durch P + 1. Wenn wir P + 1 anstelle von P in die Formel einsetzen, erhalten wir Folgendes: \[f(P+1,Q+1) = f(P+1,Q) + f(P,Q) + f(P-1,Q) + \ldots + f(0,Q)\] \[f(P+1,Q+1) = f(P+1,Q) + f(P,Q+1)\]Aus dieser neuen Ableitung können wir die Formel \(f(P,Q) = f(P,Q-1) + f(P-1,Q)\) wo \(f(P,0) = 1\) und \(f(0,Q) = 1\).
- Eine alternative Herleitung einer rekursiven Formel
  - Es gibt oft mehrere Möglichkeiten, bei kombinatorischen Problemen zu zählen. Die folgende Ableitung bietet eine andere und elegantere Möglichkeit, die Formel abzuleiten.
  - Wir verwenden die gleiche Darstellung, die wir zuvor verwendet haben, wobei wir die Gesamtzahl der Pfade finden möchten, die uns von (P,0) nach (0,Q) führen. Wir können diese Pfade in zwei Gruppen einteilen.
  - Pfade, die mit dem ersten Zug beginnen, der von (P,0) nach (P,1) nach rechts führt. Wir wissen, dass wir in dieser Gruppe insgesamt f(P,Q-1)-Pfade von (P,1) bis (0,Q) haben. Wir wissen das, weil das verbleibende Rechteck nach dem Verschieben nach rechts die Größe P x (Q-1) hat.
  - Die andere Gruppe sind Pfade, die mit dem ersten Zug beginnen und einen Zug von (P,0) nach (P-1,0) gehen. In dieser Gruppe wissen wir, dass es f(P-1,Q) Gesamtpfade gibt, da das resultierende Rechteck die Größe (P-1) x Q hat.
  - Da also jeder mögliche Pfad in eine dieser beiden Gruppen fällt, ist die Gesamtzahl der Pfade die Summe dieser Gruppen. Daraus ergibt sich die gleiche Formel \(f(P,Q) = f(P,Q-1) + f(P-1,Q)\).
- Ableitung einer expliziten Formel
  - Anstatt Pfade in der unteren rechten Ecke zu beginnen, drehen wir das Rechteck so, dass sich der Punkt (P,0) oben befindet. Wir können nun die Pfade anhand des folgenden Diagramms visualisieren:
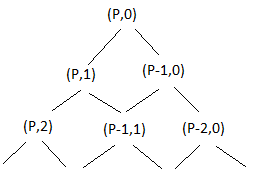
  - Diese Art von Diagramm wird als Baum bezeichnet. Dieses Muster wiederholt sich so lange, bis wir von (P,0) nach (0,Q) gereist sind. Wenn das passiert, enthält der Baum alle möglichen Pfade, die man auf der ganzen Linie einschlagen kann.
  - Die Anzahl der Möglichkeiten, um von oben (P,1) zu einem Knoten (I,J) in diesem Baum zu gelangen, ist die Anzahl der Wege, um zu (I-1,J) zu gelangen, und dann nach rechts hinunter zu (I,J), plus die Anzahl der Wege, um zu (I,J-1) zu gelangen, und dann nach links hinunter zu (I,J). Mit anderen Worten, dies ist die Zahl im Pascalschen Dreieck.
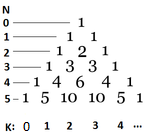
  - Jede Zahl im Pascalschen Dreieck ist die Summe der beiden oben genannten Zahlen. Die Zahlen in der linken Spalte zählen die Reihen des Bretts, beginnend bei 0 mit einem leeren Brett. Die Zahlen unterhalb des Dreiecks stellen die Position von links dar, ebenfalls beginnend bei 0. Die Zahl in der N-ten Zeile an der Position K ist gleich \({N \choose K} = \frac{N!}{(N-K)!K!}\).
  - Wir wollen die Zahl f(p,q) finden, die die Anzahl der Wege ist, um von (P,0) nach (0,Q) zu gelangen. Um das zu tun, muss man von oben P mal rechts und Q mal links unten gehen. Mit der Baumstruktur, die wir zuvor definiert haben, ist dies dasselbe, als würde man von (0,0) nach (P,Q) gehen, wobei man im Baum nur nach links und rechts geht.
  - Dies führt jedoch dazu, dass wir P+Q-Schritte machen, sodass wir uns in der Zeile P+Q im Baum befinden. Da wir wissen, dass wir Q mal nach rechts verschoben haben, ist die Zahl im Pascalschen Dreieck an dieser Stelle \({P+Q \choose Q} = \frac{(P+Q)!}{P!Q!}\).
- Nachweis der expliziten Formel durch Induktion
  - Wir werden zeigen, dass die folgenden Formeln äquivalent sind. \[f(P,Q) = \begin{cases}1 & for & P=0 \\1 & for & Q=0 \\f(P,Q-1) + f(P-1,Q) & for & \text{P>0 and Q>0}\end{cases} = \Bigg\{{P+Q \choose Q} = \frac{(P+Q)!}{P!Q!}\]
  - Induktionsbasis: Wir wissen bereits, dass f(0,0) = 1 durch die Formeldefinition ist. Wenn wir P=0 und Q=0 in die Formel einsetzen, erhalten wir \(\frac{(0+0)!}{0!0!} = \frac{0!}{1} = 1\). Dies zeigt, dass die Basisformeln äquivalent sind, wodurch die Induktionsbasis abgeschlossen ist.
  - Induktionsvoraussetzung: Nehmen wir an, dass die Formeln für alle Werte von P,Q mit P+Q = N äquivalent sind.
  - Induktionsschritt: Mit Hilfe der Induktionshypothese beweisen wir die Äquivalenz für alle Werte P,Q mit P+Q=N+1. Für alle Werte P,Q mit P+Q=N+1 haben wir 3 Fälle:
  - Fall 1:
  - Fall 2:
  - Fall 3: \(P,Q > 0\) \[ \begin{align} f(P,Q) &= f(P,Q-1) + f(P-1,Q)\qquad\qquad (+)\\ &= \frac{(P+Q-1)!}{P!(Q-1)!} + \frac{(P-1+Q)!}{(P-1)!Q!}\\ &= \frac{(P+Q-1)!Q}{P!(Q-1)!Q} + \frac{(P-1+Q)!P}{(P-1)!PQ!}\\ &= \frac{(P+Q-1)!}{P!Q!} (Q+P)\\ &= \frac{(P+Q)!}{P!Q!} \end{align} \]
  - (+): Wenn P + Q = N + 1, dann P + Q-1 = N, d.h. durch Induktionshypothese.
    f(P,Q-1) = \(\frac{(P+(Q-1))!}{(P!(Q-1)!)}\), und ähnlich für f(P-1, Q)
  - Dies zeigt, dass die beiden Formeln für f(P,Q) äquivalent sind.
  - Ende des Beweises. ∎

Wie viele verschiedene Positionen haben P-Zeilen und Q-Spalten?
- Man kann einfach die gleiche Formel für alle Positionen verwenden, die in ein Rechteck mit P-1-Zeilen und Q-1-Spalten passen, nämlich f(P-1,Q-1).

Gibt es mehr Gewinn- oder mehr Verlustpositionen?

# der Kacheln	# der Positionen	# der Verlustpositionen	% der Verlustpositionen
20	627	42	6.69
30	5604	220	3.92
40	37338	1022	2.73
50	204226	4976	2.43
60	966467	20106	2.08
70	4087968	76688	1.87
80	15796476	270142	1.71
90	56634173	897964	1.58

Eine Hypothese von Caribou

Zuvor haben wir gezeigt, dass jede Position entweder eine Gewinn- oder eine Verlustposition ist. Der Beweis gab uns eine direkte Methode, um Schritt für Schritt für alle Positionen festzustellen, ob sie verlieren oder gewinnen. Das Besondere ist, dass diese Methode keine Suche (Ausprobieren von Zügen) benötigte. Es erinnerte uns an das "Sieb des Eratosthenes", um alle Primzahlen bis zu einer gewissen Größe zu bestimmen.

Lesen Sie mehr über das Sieb des Eratosthenes, zum Beispiel im Internet
- Um alle Primzahlen bis zur Größe N² zu finden, wobei N eine ganze Zahl ist, würde man folgendermaßen vorgehen:
- - A: Beginnen Sie mit der Primzahl p=2.
  - B: Alle Vielfachen von p bis N² durchstreichen.
  - C: Finde die nächstgrößere Zahl > p, die noch nicht durchgestrichen ist. Wenn diese Zahl > N ist, stoppt der Algorithmus. Andernfalls rufen Sie diese Nummer p an und fahren Sie mit Schritt B fort.
- Alle Zahlen bis N 2, die nicht durchgestrichen sind, sind alle Primzahlen < N². Eine Simulation dieses Algorithmus finden Sie auf https://en.wikipedia.org/wiki/Sieve_of_Eratosthenes

Diese Analogie inspirierte uns dazu, über weitere Ähnlichkeiten zwischen Primzahlen und Verlustpositionen nachzudenken. Dies führte zu einer Hypothese für verlorene Positionen, die dem "Primzahlsatz" ähnelt. Hier sind die Details.

Tabelle: Analogien zwischen Verlustpositionen in Chomp- und Primzahlen:

Zahlen	Kauen
Es gibt unendlich viele ganze Zahlen.	Es gibt unendlich viele Chomp-Positionen.
Es gibt Primzahlen und faktorisierbare Zahlen.	Es gibt Verlustpositionen und Gewinnpositionen.
Es gibt unendlich viele Primzahlen.	Es gibt unendlich viele Verlustpositionen.
Eine faktorisierbare Zahl ist das Produkt einer Primzahl und einer Zahl.	Eine Gewinnstellung ist die Summe aus einer Verlustposition und einer Position (denn was bei einem Zug ausgeschnitten wird, hat die Form einer Treppe und ist daher eine Position).
Sobald eine Primzahl bekannt ist, kennt man sofort unendlich viele faktorisierbare Zahlen (alle Vielfache der Primzahl).	Sobald eine Verlustposition bekannt ist, kennt man sofort unendlich viele Gewinnpositionen (alle Positionen, die sich aus dem Füllen von Eckrechtecken ergeben, einschließlich der unendlich langen entlang der oberen Reihe und der linken Spalte).
Es ist viel wahrscheinlicher, dass eine große Zahl durch eine kleine Primzahl teilbar ist als durch eine große Primzahl.	Es ist viel wahrscheinlicher, dass eine große Position auf eine kleine Verlustposition reduziert werden kann als auf eine große Verlustposition.
Um festzustellen, ob eine Zahl N eine Primzahl ist, ist es sehr effizient, alle Primzahlen P bis zur Quadratwurzel von N zu kennen. Dann kann man prüfen, ob N durch Division, also durch eine Probedivision N/P, auf P reduziert werden kann.	Um festzustellen, ob eine Position P eine Verlustposition ist, ist es notwendig, alle Verlustpositionen L zu kennen, die in P enthalten sind. Man kann dann effizient prüfen, ob P in einem Zug auf L reduziert werden kann.
Das "Sieb des Eratosthenes" ist eine effiziente Methode, um alle Primzahlen bis zu einer bestimmten Zahl N zu bestimmen, aber auch um zu überprüfen, ob eine gegebene Zahl eine Primzahl ist. Dieser Algorithmus ist oben beschrieben.	Ähnlich wie beim "Sieb des Eratosthenes" beginnt man mit der {1} der Verliererstellung und streicht alle Gewinnstellungen durch, die sich in einem Zug auf diese Verluststellung reduzieren. Man inspiziert dann alle Positionen mit einer weiteren Kachel. Alle Positionen, die nicht durchgestrichen sind, sind Verlustpositionen.
Die verbleibende Ineffizienz des Siebalgorithmus besteht darin, faktorisierbare Zahlen wiederholt durchzustreichen.	Die verbleibende Ineffizienz des Siebalgorithmus besteht darin, Gewinnpositionen wiederholt durchzustreichen.
Die Dichte von Primzahlen nimmt mit ihrer Größe ab; d.h. das Verhältnis (# von Primzahlen bis zu einer ganzen Zahl N) / N nimmt mit zunehmendem N ab.	Die Dichte der Verlustpositionen nimmt mit ihrer Größe ab; d.h. das Verhältnis (# der Verlustpositionen mit bis zu N Kacheln) / (# aller Positionen mit N Plättchen) nimmt mit zunehmendem N ab. (Herausforderung: Wie lautet die Formel für die Abhängigkeit dieses Verhältnisses von N und wie verhält sich das im Vergleich zur Formel für die Dichte der Primzahlen?).
Satz der Primzahlen: (# der Primzahlen ≤ N) / (N / log(N)) → 1 als N → unendlich.	Analoge Hypothese: (# der Verlustpositionen mit N Kacheln) / ((# der Positionen mit N Kacheln) / log(# der Positionen mit N Kacheln)) → 0,283... wie N → unendlich.

Tabelle: Unterschiede zwischen Verlustpositionen in Chomp und Primzahlen:

Zahlen	Kauen
Die Menge aller ganzen Zahlen ist eine vollständig geordnete Menge; d.h. zwischen zwei beliebigen Zahlen weiß man, welche größer ist.	Die Menge aller Chomp-Positionen ist eine teilweise geordnete Menge. Positionen können vollständig in anderen Positionen enthalten sein, müssen es aber nicht.
Die Operation, um eine Zahl auf einen ihrer Primfaktoren zu reduzieren, ist die Division.	Die Operation, um eine Position auf eine Verlustposition zu reduzieren, ist die Subtraktion von Kacheln.
Eine Zahl kann als Liniensegment auf einem eindimensionalen Zahlenstrahl visualisiert werden.	Eine Position wird durch eine Liste von Zahlen definiert, die nach Größe sortiert sind, und ist somit ein 2D-Objekt.

Offene Fragen:

Ist die Hypothese (# der Verlustpositionen mit N Kacheln) / ((# der Positionen mit N Kacheln) / log(# der Positionen mit N Kacheln)) → 0,283... als N → unendlich wahr?

Können Sie es beweisen? (Das können wir noch nicht :-) )

Das oben gespielte Chomp-Spiel ist eine Version von 2D Chomp. Das bedeutet, dass die Platine nur 2-dimensional ist und eine Breite und eine Höhe hat.

Könntest du dir eine Version von 3D Chomp vorstellen?
- Der einfachste Weg, sich vorzustellen, dem Spiel eine neue Dimension hinzuzufügen, besteht darin, dem Spielbrett eine dritte Dimension hinzuzufügen. Statt nur einer Breite und einer Höhe hätte das neue Brett eine Länge, eine Breite und eine Höhe. Wenn man kleine Würfel zum Spielen hätte, wie z.B. Würfel, könnte man dieses 3D-Spiel spielen, wie im Bild unten gezeigt.
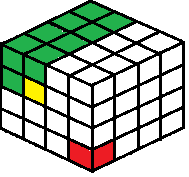
- Wenn man einen Zug macht, entfernt man den ausgewählten Würfel sowie jeden Würfel links, über und oben vom ausgewählten Würfel. Ein Beispielzug wird im Bild gelb hervorgehoben, wodurch auch alle grünen Kacheln im Bild entfernt werden. Die Person, die das letzte Plättchen nimmt, das durch die rote Kachel im Bild angezeigt wird, ist der Spieler, der das Spiel verliert.
- Um das Spielen mit echten Würfeln zu erleichtern, kann man die Würfel gegen eine Ecke, z.B. die Ecke eines Schuhkartons, schieben, so dass sich das rote Plättchen in der äußersten Ecke der Schachtel befindet und erst zugänglich ist, wenn auch alle anderen Würfel entfernt wurden. Die Verwendung eines Kastens ist nicht notwendig, aber er würde die Würfel stabilisieren und es einfacher machen, den Würfel zu entfernen, ohne die gesamte Struktur umzustoßen.

Wie wäre es, Chomp in noch mehr Dimensionen zu spielen?
- Wir haben bereits festgestellt, dass es einfach genug ist, einem Chomp-Spiel eine neue Dimension hinzuzufügen. Wenn man Chomp in einer noch höheren Dimension als 3D spielen wollte, würde man dem Chomp-Brett immer wieder neue Dimensionen hinzufügen. Nach 3D gibt es jedoch keine Möglichkeit mehr, ein Chomp-Brett mit Blöcken zu simulieren. Es gibt jedoch eine Möglichkeit, das Spiel mit Bleistift und Papier zu simulieren, und diese Methode ermöglicht es uns, das Spiel in einer beliebigen Anzahl von Dimensionen zu spielen, nicht nur in 2D oder 3D.
- Wir beginnen mit einer Partie 2D Chomp auf Papier. Eine Möglichkeit, das Spiel zu simulieren, besteht darin, zunächst eine Zahl auszuwählen, die nur 2 verschiedene Primfaktoren hat. Beispiel: 72 = 2 3 x³ ². Wir schreiben dann alle Faktoren dieser Zahl in Form eines Rechtecks auf, wie unten gezeigt.
- 72 36 18 9
  24 12 6 3
  8 4 2 1
- Jede rechte Nachbarzahl ist um den Faktor 2 kleiner und jede benachbarte Zahl darunter ist um den Faktor 3 kleiner. Um auf diesem Brett einen Zug zu machen, würde man eine Zahl auswählen. Sie würden dann diese Zahl zusammen mit allen ihren Faktoren entfernen. Wer die Zahl 72 nimmt, verliert das Spiel.
- Um ein größeres Anfangsrechteck zu erhalten, könnte man eine größere Zahl finden, indem man die Formel 2^P x 3^Q verwendet. Durch das Ersetzen von P und Q durch größere Zahlen erhält man immer größere Spielbretter für 2D-Chomp.
- Wie kann man diese Simulation für höhere Dimensionen verallgemeinern?
  - Um diese Bleistift- und Papierversion von Chomp von 2D auf 3D zu erweitern, muss man lediglich die Formel erweitern, die zur Ermittlung der Startnummer verwendet wird. Anstatt eine Zahl zu wählen, die nur 2 verschiedene Primfaktoren hat, würde man eine Zahl wählen, die 3 verschiedene Primfaktoren hat. Wir können eine neue Formel verwenden, um diese Zahl zu finden, die wie folgt lautet: 2^P x 3^Q x 5^R. Dann kann das Spiel mit den gleichen Methoden wie zuvor in 3 Dimensionen simuliert werden. Um zu noch größeren Dimensionen zu gelangen, müssen Sie der Formel einfach neue Primzahlen hinzufügen, abhängig von der Anzahl der gewünschten Dimensionen.