Chomp
Jumlah bilangan permainan: 1848453
Jumlah kemenangan: 160507
Jumlah kemenangan: 160507
Cara Bermain:
- Permainan ini dimainkan oleh dua pemain, sama ada anda dan rakan, atau anda menentang komputer.
- Setiap pemain akan bergilir-gilir mengambil gula-gula dari petak di bawah.
- Apabila sekeping gula-gula dipilih, semua gula-gula di bawah dan di sebelah kanan gula tersebut juga dikeluarkan dari papan.
Cara Menang:
- Pemain yang mengambil gula-gula terakhir dari kedudukan kiri atas sekali kalah.
Tiada komen buat masa ini
Giliran Pemain 1
Access to 'Some food for thought' (SFFT) for the iChomp game can be purchased in the online shop
Jika anda hanya mahu menjadi lebih baik dalam permainan secepat mungkin kemudian terus ke 'Lebih Banyak Mengenai Cara Bermain' >> 'Bagaimana untuk belajar kehilangan kedudukan dengan komputer?'.
Makanan berikut untuk pemikiran berbeza dalam kesukaran. Sebahagian daripadanya sesuai untuk pelajar sekolah rendah, sebagai contoh, item "Mari Cuba Sesuatu". Item lain menunjukkan bukti matematik dan faedah yang mungkin diperoleh daripada mereka. Ini adalah bahan sekolah menengah. Sila lihat sendiri apa yang sesuai untuk anda atau Kelab Matematik Sekolah Caribou anda.
Anda memanfaatkan sepenuhnya aktiviti dengan berfikir terlebih dahulu sebelum mengembangkan jawapan kepada soalan-soalan.
Selamat bercuba.
- Medan ialah titik silang baris dan lajur, dilabelkan (baris, lajur).
- Jubin adalah gambar pada beberapa medan.
- Kedudukan terdiri daripada semua bidang dengan jubin.
- Mari kita mulakan dengan soalan mudah, iaitu kedudukan kecil. Untuk menciptanya, kita klik 'Komputer: Henti'. Jika kita kemudian klik pada (2,1) hanya satu baris jubin yang tersisa.
-
- Dengan mengklik pada (1,2) hanya jubin pada (1,1) yang tersisa, jadi anda kalah.
- Marilah kita klik 'Permainan Baru' dan pada (3,1) dan (2,2) untuk mempunyai satu jubin dalam baris 2 dan semua baris 1.
-
- Dengan mengklik pada (1,3) hanya tiga jubin yang tersisa. Bolehkah anda melihat bahawa anda tidak mempunyai peluang?
- Mari klik pada 'Permainan Baru' dan klik pada (3,1) dan (2,3).
-
- Lawan anda boleh klik pada (1,4). Bolehkah anda melihat bahawa anda tidak mempunyai peluang?
-
 Bolehkah anda meringkaskan kedudukan mana dengan jubin dalam hanya 2 baris anda tidak mempunyai peluang untuk memenangi permainan?
Bolehkah anda meringkaskan kedudukan mana dengan jubin dalam hanya 2 baris anda tidak mempunyai peluang untuk memenangi permainan?
- Jika baris atas mempunyai satu jubin lebih daripada baris ke-2, maka tidak kira apa yang anda lakukan, lawan anda sentiasa boleh bergerak supaya baris atas mempunyai satu jubin lebih daripada baris ke-2. Kemudian tidak kira apa yang anda lakukan, akhirnya anda perlu memilih jubin (1,1) dan kalah dalam permainan.
- Jika jubin diklik, semua jubin di bawah dan di sebelah kanan juga dikeluarkan. Peraturan ini mempunyai simetri; iaitu keseluruhan permainan mempunyai simetri berikut: Jika kita menukar baris dan lajur maka peraturan tetap sama: semua jubin di sebelah kanan menjadi semua jubin di bawah dan semua jubin di bawah menjadi semua jubin di bawah menjadi semua jubin di sebelah kanan jubin dikeluarkan. Dalam erti kata lain, jika kita mencerminkan kedudukan di sepanjang garis yang melalui (1,1) dan (2,2) maka kedudukan baru mungkin kelihatan berbeza, tetapi ia mempunyai status yang sama. Langkah menang juga akan menjadi langkah yang sama, hanya dicerminkan juga.
-
 Kedudukan dengan 3 jubin dalam baris pertama dan 2 jubin dalam baris kedua tidak ada harapan, seperti yang kita tahu. Apakah jubin yang ada pada kedudukan cermin?
Kedudukan dengan 3 jubin dalam baris pertama dan 2 jubin dalam baris kedua tidak ada harapan, seperti yang kita tahu. Apakah jubin yang ada pada kedudukan cermin?
- Selepas mencerminkannya mempunyai 3 jubin di lajur kiri dan 2 jubin dalam lajur ke-2.
-
 Kita tahu semua kedudukan tanpa harapan mempunyai jubin hanya dalam dua baris pertama. Apakah simetri memberitahu kita tentang semua kedudukan tanpa harapan dengan jubin hanya dalam dua lajur pertama?
Kita tahu semua kedudukan tanpa harapan mempunyai jubin hanya dalam dua baris pertama. Apakah simetri memberitahu kita tentang semua kedudukan tanpa harapan dengan jubin hanya dalam dua lajur pertama?
- Posisi tanpa harapan dengan jubin dalam dua lajur pertama ialah tempat lajur pertama mempunyai satu jubin lebih daripada lajur kedua.
- Berikut adalah kedudukan lain tanpa peluang: Klik 'Permainan Baru' dan pada (4,1), (2,2) dan (1,4).
-
- Anda perlu memastikan bahawa selepas anda mengalihkan baris atas dan lajur pertama sekali lagi mempunyai panjang yang sama. Dengan mengulangi corak ini, pemain lawan akhirnya perlu mengambil jubin (1,1) dan kalah.
-
 Jadi, jika baris pertama dan lajur pertama mempunyai bilangan jubin yang sama dan tidak ada jubin lain maka kedudukan itu tidak ada harapan. Kedudukan manakah yang boleh diubah menjadi kedudukan sedemikian?
Jadi, jika baris pertama dan lajur pertama mempunyai bilangan jubin yang sama dan tidak ada jubin lain maka kedudukan itu tidak ada harapan. Kedudukan manakah yang boleh diubah menjadi kedudukan sedemikian?
- Jika kedudukan mempunyai bilangan baris dan lajur yang sama, tidak kira berapa banyak jubin yang terdapat di tempat lain: bergerak pada (2,2) meninggalkan hanya baris pertama dan lajur pertama dengan panjang yang sama, meninggalkan pemain lawan tiada peluang. Jadi jika kedudukan mempunyai bilangan jubin yang sama di baris atas seperti dalam lajur kiri maka anda bermain di (2,2) dan memenangi permainan.
- Untuk bermain Chomp dengan baik, seseorang perlu tahu tentang menang dan kehilangan kedudukan. Kedudukan yang menang adalah salah satu di mana seseorang boleh menguatkuasakan kemenangan jika seseorang bermain secara optimum, tidak kira apa yang pihak lain lakukan. Kedudukan kalah adalah satu di mana seseorang tidak mempunyai peluang jika pemain lain bermain secara optimum. Perkara-perkara berikut adalah apa yang dipanggil dalam matematik definisi. Dalam Chomp, kedudukan kalah dan menang ditakrifkan melalui 3 mata ini:
- Jika hanya satu jubin yang tersisa (di sudut kiri atas), maka ini adalah kedudukan yang kalah.
- Kedudukan adalah kedudukan yang menang jika wujud gerakan yang mengakibatkan kedudukan kalah bagi pemain lawan.
- Kedudukan adalah kedudukan kalah jika setiap gerakan menghasilkan kedudukan kemenangan untuk pemain lawan.
- Pada pandangan pertama kedudukan di atas mungkin kelihatan tidak berguna kerana kedudukan kemenangan dijelaskan oleh kedudukan kalah, dan kedudukan kalah dijelaskan oleh kedudukan kemenangan. Walau bagaimanapun, definisi ini berdasarkan pergerakan prestasi, dan setiap urutan pergerakan akhirnya membawa kepada kedudukan jubin tunggal yang mengikut titik 1 adalah kedudukan yang kalah.
-
 Adakah mungkin terdapat kedudukan di mana kedua-dua pihak tidak boleh menguatkuasakan kemenangan? (sukar)
Adakah mungkin terdapat kedudukan di mana kedua-dua pihak tidak boleh menguatkuasakan kemenangan? (sukar)
- Kita akan merumuskan teorem kecil dan membuktikannya. Bukti akan menunjukkan kepada kita cara bagaimana untuk mencapai kekuatan bermain yang sempurna. Bukti adalah bukti dengan induksi di mana seseorang menunjukkan bahawa pernyataan yang ingin kita buktikan adalah benar untuk satu jubin dan kemudian menunjukkan bahawa jika benar untuk mana-mana nombor N jubin maka ia juga mesti benar untuk satu lagi jubin, iaitu jubin N + 1. Oleh kerana pernyataan ini benar untuk jubin N = 1, ia mesti benar untuk jubin N + 1 = 1 = 1 = 2. Tetapi menjadi benar untuk N = 2, ia juga mesti benar untuk N + 1 = 2 + 1 = 3 jubin, dan sebagainya; iaitu untuk sebarang bilangan jubin.
- Lemma (teorem kecil): Setiap kedudukan adalah sama ada menang atau kedudukan kalah.
- Bukti oleh induksi:
- Pangkalan Induksi: Jika kedudukan hanya mempunyai satu jubin maka jubin ini berada di sudut kiri atas dan kemudian kedudukan itu adalah kedudukan yang kalah mengikut peraturan Chomp (menunjukkan bahawa lemma adalah benar jika hanya jubin N = 1 hadir).
- Hipotesis induksi: Kita menganggap lemma adalah benar untuk semua kedudukan dengan sehingga N, iaitu kedudukan dengan 1,2,..., N jubin sama ada menang atau kalah kedudukan.
- Langkah induksi: Kita kini mahu menunjukkan bahawa semua kedudukan dengan N+1 mesti sama ada kalah atau menang.
- Dalam P berikut adalah kedudukan sewenang-wenangnya dengan jubin N + 1. Jika P dikurangkan dengan satu langkah maka kedudukan baru mesti mempunyai jubin ≤N, jadi ia adalah kedudukan kalah atau menang mengikut hipotesis induksi. Jika P boleh dikurangkan dalam satu langkah ke kedudukan kalah maka P adalah kedudukan yang menang. Jika tidak, maka P boleh dikurangkan dalam satu langkah hanya ke kedudukan yang menang. Tetapi jika kedudukan boleh dikurangkan dalam bergerak hanya ke kedudukan yang menang maka P mestilah kedudukan yang kalah. Ini membuktikan bahawa P (mempunyai jubin N + 1) sama ada menang atau kedudukan kalah. Ini menunjukkan bahawa semua kedudukan (dengan N+2,N+3,... jubin) sama ada menang atau kalah kedudukan.
Akhir Bukti ∎ - Komen Tambahan: Langkah induksi menyediakan kaedah untuk memutuskan semua kedudukan (sehingga beberapa saiz) sama ada mereka menang atau kehilangan kedudukan. Ia ditakrifkan oleh yang berikut:
Satu bermula dengan N = 1 dan melabelkan kedudukan itu sebagai kedudukan yang kalah. Satu kemudian menentukan status semua kedudukan dengan 2 jubin, kemudian dengan 3 jubin dan sebagainya, setiap kali menggunakan pengetahuan tentang status kedudukan yang lebih kecil, dan menambah kedudukan kehilangan yang baru dijumpai ke senarai kedudukan yang diketahui kalah. - Ini adalah cara yang sangat berkesan untuk mencari semua kedudukan yang menang dan kalah sehingga beberapa saiz. Oleh kerana bilangannya semakin besar, program komputer akan membantu. Bahan-bahan yang diperlukan adalah seperti berikut:
- Prosedur yang dapat mencipta semua kedudukan jubin N dengan cekap daripada mengetahui semua kedudukan kurang daripada jubin N
- Prosedur yang dapat memeriksa dengan cekap sama ada kedudukan boleh dikurangkan ke kedudukan lain yang diberikan atau tidak.
-
- Terdapat hanya dua kedudukan yang mungkin mempunyai tepat 2 jubin, 2 jubin di baris atas, atau dua jubin di sepanjang lajur kiri. Kedua-dua jawatan ini adalah kedudukan yang menang.
-
- Terdapat 3 jumlah kedudukan yang mungkin mempunyai tepat 3 jubin. Mereka terdiri daripada 2 kedudukan yang menang, dan 1 kedudukan kalah. Bolehkah anda mengetahui kedudukan mana mereka?
-
- Terdapat 5 kedudukan yang mungkin mempunyai tepat 4 jubin. Semua kedudukan ini adalah kedudukan yang menang.
-
- Terdapat 7 jumlah kedudukan yang mungkin mempunyai tepat 5 jubin. Dari kedudukan ini, 3 kehilangan kedudukan dan 4 memenangi kedudukan. Bolehkah anda mengetahui yang mana mereka?
-
- Lemma berikut menjawab soalan ini. Bukti adalah bukti kewujudan. Ia hanya akan membuktikan kewujudan langkah menang tanpa menunjukkan apa langkah itu. Walau bagaimanapun, mengetahui lemma berguna untuk permainan anda seperti yang dijelaskan di bawah.
- Lemma: Semua kedudukan segi empat tepat kecuali kedudukan 1 jubin adalah kedudukan yang menang.
- Bukti: Untuk menunjukkan ini adalah benar, kita perlu mempertimbangkan dua kes yang mungkin:
- Mengeluarkan jubin di sudut kanan bawah papan adalah langkah yang menang.
- Mengeluarkan jubin di sudut kanan bawah bukanlah langkah yang menang.
- Jika kes 1 adalah benar, maka itu bermakna segi empat tepat adalah kedudukan yang menang, dan ini menyokong lemma.
- Jika kes 1 tidak benar, maka kita perlu mempertimbangkan kes 2. Mengikut bukti yang kami lakukan sebelum ini, kedudukan yang terhasil daripada mengeluarkan jubin di sudut kanan bawah mesti menjadi kedudukan yang menang, yang bermaksud ia mesti mempunyai langkah menang yang wujud. Tetapi, kerana setiap pergerakan dalam segi empat tepat menghilangkan jubin di sudut kanan bawah, kedudukan kalah yang terhasil daripada gerakan ke-2 (langkah kemenangan) adalah sama sama ada gerakan kemenangan dimainkan selepas pergerakan sudut atau bukannya gerakan sudut. Ini bermakna bahawa langkah kemenangan boleh dimainkan dengan segera, sekali gus membuktikan bahawa langkah kemenangan wujud untuk kedudukan segi empat tepat.
- Akhir Bukti ∎
- Komen tambahan: Walaupun lemma tidak memberitahu kita apa langkah kemenangan, sudah berguna untuk mengetahui bahawa kedudukan segi empat tepat memenangi kedudukan. Oleh itu, seseorang tidak boleh membuat langkah yang mewujudkan kedudukan segi empat tepat (kecuali kedudukan 1x1).
-
- Untuk semua segi empat sama saiz >1 satu-satunya langkah kemenangan ialah pada (2,2).
-
 Untuk kedudukan mana yang serupa dengan segi empat sama adalah langkah yang sama dengan langkah menang?
Untuk kedudukan mana yang serupa dengan segi empat sama adalah langkah yang sama dengan langkah menang?
- Pergerakan (2,2) juga merupakan langkah menang untuk sebarang kedudukan di mana baris 1 dan lajur 1 mempunyai panjang yang sama.
-
- Ya kedudukan boleh mempunyai lebih daripada satu langkah menang. Pertimbangkan kedudukan berikut:
###
##
#
Kedudukan lembaga ini mempunyai 3 gerakan kemenangan berbeza yang boleh dibuat. Bolehkah anda menentukan apa itu?
- Ya kedudukan boleh mempunyai lebih daripada satu langkah menang. Pertimbangkan kedudukan berikut:
- Strategi umum untuk menang di Chomp adalah untuk mencipta kedudukan kalah untuk lawan anda supaya mereka tidak mempunyai peluang. Kita juga mahu mengelak daripada mencipta kedudukan kemenangan yang pihak lawan boleh kembali menjadi kehilangan kedudukan buat kita.
- Kunci untuk menang adalah mengetahui sebanyak mungkin kehilangan kedudukan, dan untuk mengesan cara membuatnya sebelum lawan anda melakukannya. Mari kita pertimbangkan papan yang mungkin berikut, yang merupakan kedudukan kehilangan yang diketahui:
#######
###
###
#
#
- Rajah 1
-
- Kehilangan kedudukan di atas boleh disebabkan oleh sebarang pergerakan yang ditandakan dengan + di bawah:
Rajah 2 Langkah-langkah ini semuanya terletak di sudut-sudut yang dipotong. Mana-mana + bergerak sedemikian juga akan memotong jubin yang mungkin muncul dalam imej di bawah dengan ?:#######+
###
###
#
########
###+
###
#
########
###
###
#+
########
###
###
#
#
+ -
Rajah 3#######+?
###
###
#
########
###+???
###????
#
########
###
###
#+?
#??#######
###
###
#
#
+
? - + jubin diperlukan, dan ? jubin adalah pilihan. Dalam kedudukan kemenangan kiri, baris atas boleh dilanjutkan sewenang-wenangnya ke kanan dengan lebih banyak '?', dan dalam kedudukan kemenangan yang betul, lajur pertama boleh dilanjutkan sewenang-wenangnya ke bahagian bawah dengan lebih banyak '?'. Semua jawatan ini juga memenangi kedudukan. Sekiranya kita bergerak dalam kedudukan sedemikian, kita akan mengambil + jubin, dan oleh itu semua ? jubin yang disambungkan juga akan dikeluarkan, mengakibatkan kedudukan kehilangan yang kami mulakan.
- Kehilangan kedudukan di atas boleh disebabkan oleh sebarang pergerakan yang ditandakan dengan + di bawah:
-
- Bagi setiap kedudukan yang kalah terdapat banyak kedudukan yang boleh diubah menjadi kedudukan kalah ini dengan satu langkah. Oleh itu, semua jawatan yang tidak terhingga banyak memenangi kedudukan.
- Sebarang kedudukan mempunyai sekurang-kurangnya 2 penjuru. Kedudukan kalah dalam Rajah 1 mempunyai 4 penjuru yang merupakan tempat di mana a + ditunjukkan dalam Rajah 2. Sebarang kedudukan yang mempunyai # di + dan mungkin #'s di sebelah kanan + dan / atau di bawah + (di mana pada masa ini ? ditunjukkan dalam Rajah 3), semuanya akan ditukar kepada kedudukan yang kalah apabila + diklik.
- Dalam kedudukan dengan + di baris atas (gambar rajah paling kiri dalam Rajah 3) boleh menjadi 0, 1, 2, 3, ... banyak # di sebelah kanannya. Semua kedudukan yang tidak terhingga ini akan berubah menjadi kedudukan kalah tunggal dengan mengklik +. Begitu juga, dalam gambarajah paling kanan Rajah 3, di bawah + boleh ada sewenang-wenangnya banyak salib berganda dan semua kedudukan yang tak terhingga ini berubah menjadi kedudukan kalah tunggal dengan mengklik +
- Oleh itu, terdapat lebih banyak kedudukan yang menang daripada kehilangan kedudukan. Oleh itu, adalah paling berkesan untuk mengingati seberapa banyak kehilangan kedudukan yang mungkin, semua kedudukan lain memenangi kedudukan.
-
 Buat senarai kehilangan kedudukan yang anda tahu, dan untuk setiap kedudukan tulis semua kedudukan kemenangan yang sepadan dan bagaimana untuk mengesannya
Buat senarai kehilangan kedudukan yang anda tahu, dan untuk setiap kedudukan tulis semua kedudukan kemenangan yang sepadan dan bagaimana untuk mengesannya
- Contoh berikut menunjukkan apa yang kami maksudkan:
- Seperti yang ditunjukkan sebelum ini, apabila kedudukan hanya mempunyai 2 baris, dan baris atas mempunyai satu jubin lebih daripada baris kedua, daripada ini adalah kedudukan kalah, seperti yang ditunjukkan di bawah:
- #####
#### - Mengambil kedudukan kalah yang diketahui ini, kita boleh menentukan bahawa kedudukan kemenangan yang sepadan adalah:
-
#####+?
#########
####+#####
####
+???
???? - Di kedudukan kiri, boleh ada nombor? di sebelah kanan baris atas, dan di kedudukan yang betul, boleh ada bilangan baris? di bawahnya. Kita boleh meringkaskan dengan kata-kata bagaimana untuk mengesan kedudukan kemenangan ini (yang harus anda ingat untuk permainan anda):
-
- Kedudukan adalah kedudukan yang menang yang berkurangan kepada
#####
#### - - Jika sama ada kedudukan hanya mempunyai dua baris, dan baris pertama tidak betul-betul satu jubin lebih lama maka baris kedua, atau
- - Jika kedudukan mempunyai lebih daripada dua baris, dan baris pertama adalah betul-betul satu jubin lebih lama maka baris kedua.
- Kedudukan adalah kedudukan yang menang yang berkurangan kepada
- Tetapi ada lebih banyak lagi yang perlu difikirkan juga. Kami bukan sahaja mahu bermain dengan betul di posisi kemenangan seperti itu, kami juga mahu mengelak daripada membuat langkah yang mencipta kedudukan kemenangan sedemikian. Ini bermakna kita tidak boleh membuat pergerakan di mana hanya dua baris kekal, atau di mana baris kedua mempunyai satu jubin kurang kemudian baris pertama.
- Untuk meringkaskan, kita mahu mencipta kedudukan kalah, tetapi kita juga mahu mengelak daripada mencipta kedudukan yang mana satu bergerak jauh daripada kedudukan kalah.
- Satu lagi perkara yang perlu diperhatikan: kerana simetri cermin yang disebutkan sebelumnya, semua komen di atas boleh diulang dengan hanya menggantikan perkataan "baris" dengan perkataan "lajur".
- Ia diserahkan kepada anda untuk mengumpul lebih banyak kedudukan kalah dan kedudukan kemenangan yang sepadan yang merupakan satu langkah jauh.
-
- Jika anda menyedari bahawa anda perlu bergerak dalam kedudukan yang kalah, maka secara teori anda tidak mempunyai peluang. Apa yang boleh anda lakukan ialah berharap lawan anda tidak tahu semua gerakan kemenangan untuk kedudukan yang boleh anda buat dengan langkah seterusnya. Apa yang boleh anda lakukan ialah hanya mengeluarkan jubin tunggal dari sudut. Ini memberikan lawan anda kedudukan saiz maksimum, dan ia menjadikannya lebih sukar bagi lawan anda untuk mengetahui langkah kemenangan yang sepadan.
-
- Seseorang perlu melakukan apa yang dikenali sebagai carian pokok lengkap. Pemain pertama bermula dengan meneka gerakan, kemudian pemain kedua meneka gerakan dan sebagainya sehingga seorang pemain, kata pemain A, menang. Kemudian pemain B dibenarkan menukar langkah terakhir yang mereka buat dan ia adalah giliran pemain A seterusnya. Jika dalam satu kedudukan pemain yang bermain seterusnya, katakan B, kehabisan gerakan kerana semua gerakan membawa kepada kerugian, maka ini adalah kedudukan kalah, dan pemain B boleh mengubah langkah terakhir yang dibuat sebelum kedudukan kalah ini dicapai.
- 'Pencarian pokok' ini berterusan sehingga jelas sama ada kedudukan permulaan adalah kedudukan kalah atau gerakan pemain 1 yang mengubahnya menjadi posisi kalah.
- Ini boleh menjadi proses yang sangat panjang jika seseorang cuba melakukannya pada papan awal dengan banyak jubin. Walau bagaimanapun, semakin banyak kehilangan kedudukan yang kita tahu semakin pendek urutan pergerakan sebelum kedudukan sedemikian dicapai, dan dengan itu keseluruhan carian jauh lebih cepat. Jika kita tahu semua kedudukan yang kalah, maka sama ada kedudukan permulaan akan diiktiraf sebagai kedudukan kalah, atau hanya satu langkah yang diperlukan untuk mengurangkannya ke kedudukan yang kalah.
-
- Dalam tahap kesukaran 'Sangat Keras' dan kedudukan tidak lebih besar daripada 8 x 15 komputer bermain dengan sempurna sehingga setiap kedudukan yang terhasil daripada langkah komputer adalah postion yang kalah! Seseorang harus bermula dengan papan yang sangat kecil dan bermain melawan komputer di tahap 'Sangat Keras' dan belajar semua kedudukan yang dihasilkan oleh komputer. Untuk setiap kedudukan sedemikian fikirkan bagaimana setiap langkah anda akan dijawab oleh komputer mengubahnya lagi menjadi kedudukan kehilangan yang lebih kecil. Bagi setiap kedudukan yang kalah juga kedudukan cermin (baris <--> lajur) ialah kedudukan yang kalah.
-
- Dalam pertandingan ini kedudukan permulaan akan menjadi segi empat tepat gula-gula. Seperti yang terbukti sebelum ini, segi empat tepat adalah kedudukan yang menang, tetapi apakah langkah pertama yang mengubahnya menjadi kedudukan kalah bagi lawan? Kami belajar sebelum ini bahawa langkah optimum untuk segi empat sama adalah jubin (2,2) tetapi bagaimana jika segi empat tepat bukan segi empat sama?
- Hanya tukar ke tahap kesukaran 'sangat keras' dan biarkan komputer membuat langkah pertama. Selagi segi empat tepat tidak lebih besar daripada 8x15, komputer bermain secara optimum dan akan menunjukkan langkah pertama yang sempurna. Cuba saiz segi empat tepat yang berbeza dan ingat langkah pertama yang optimum kerana permainan komputer tidak akan tersedia pada hari pertandingan :).
- Tidak lama lagi anda akan tiada tandingan dalam tahap kesukaran yang mudah dan sederhana.
-
- Kami sudah bertemu dengan dua keluarga yang kehilangan kedudukan ini. N ialah sebarang integer positif.
- N jubin dalam lajur 1 (kiri) dan jubin N dalam baris 1 (atas),
- Jubin N dalam baris 1 dan jubin N-1 dalam baris ke-2 termasuk versi cerminnya dengan lajur baris <-->.
- Berikut adalah lagi:
- Jubin 3+2N dalam baris 1, jubin 2+2N dalam lajur 1, 1 jubin pada (2,2), N>=0,
- Jubin 3+2N dalam lajur 1, 3 jubin dalam lajur ke-2, jubin 4+2N dalam baris 1,
- Jubin 6+2N dalam lajur 1, 3 jubin dalam lajur ke-2, jubin 5+2N dalam baris 1,
- serta versi cermin (baris <--> lajur) mereka.
- Pemain komputer yang dibina ke dalam permainan menggunakan teknik yang berbeza untuk tahap permainan yang berbeza.
-
- Mudah- Membuat pergerakan rawak setiap pusingan. Sekiranya kedudukan kemenangan mudah dikesan, ia akan bergerak ke sana.
- Sederhana- Masih bergerak secara rawak, tetapi mempunyai pengetahuan yang lebih besar untuk menang dan kehilangan kedudukan. Akan mengelakkan gerakan yang memberi akses kepada lawan kepada langkah kemenangan yang mudah.
- Keras- Mempunyai pengetahuan yang lebih besar untuk memenangi kedudukan. Secara aktif mencari papan untuk bergerak yang boleh memaksa lawan untuk membuat gerakan kalah sendiri.
- Sangat sukar - Akan sentiasa membuat langkah optimum untuk mana-mana kedudukan yang sesuai dengan segi empat tepat saiz 8x15.
- Semakin tinggi tahap kesukaran, semakin sukar untuk memaksa komputer menjadi kedudukan yang kalah. Setiap peringkat tahu lebih banyak kedudukan menang dan kalah daripada tahap sebelumnya, dan semakin sukar, semakin banyak kedudukan yang menang dan kalah yang perlu anda ketahui untuk mencuba dan memaksa komputer menjadi kedudukan yang kalah.
- Komen-komen berikut tidak akan membantu untuk menjadi lebih kuat di Chomp, tetapi mereka akan memberikan beberapa fakta menarik dan memberi kita satu lagi peluang untuk mengamalkan bukti dengan induksi.
-
 Berapa banyak kedudukan yang berbeza, termasuk papan kosong, dimuatkan ke dalam segi empat tepat dengan baris P dan lajur Q?
Berapa banyak kedudukan yang berbeza, termasuk papan kosong, dimuatkan ke dalam segi empat tepat dengan baris P dan lajur Q?
- Jika kita memasukkan segi empat tepat kosong, kita boleh mengira jumlah kedudukan yang mungkin menggunakan formula berikut: \[\frac{(P+Q)!}{P!Q!}\]Bolehkah anda mengira nombor itu untuk P dan Q kecil, dan mengesahkan bahawa ia betul?
-
- Biarkan f(P,Q) menjadi bilangan kedudukan dalam segi empat tepat saiz PxQ. Pemerhatian penting ialah semua kedudukan mempunyai bentuk tangga, di mana setiap baris mempunyai jubin yang paling banyak seperti baris di atas, tetapi tidak lebih.
- Mari kita mulakan terlebih dahulu dengan cara kita boleh mewakili semua tangga ini. Salah satu cara untuk membuat tangga dengan mudah adalah dengan bermula di sudut kiri bawah papan, dan sama ada bergerak ke kanan atau ke atas. Seseorang boleh terus membuat ini betul dan bergerak sehingga mereka sampai ke sudut kanan atas papan. Kami akan merujuk kepada ini sebagai jalan yang kami ambil untuk mendapatkan dari (P,0) hingga (0,Q).
- Bilangan kedudukan adalah sama dengan bilangan laluan dari (P,0) hingga (0,Q), selagi seseorang hanya dibenarkan bergerak ke atas atau ke kanan. Nombor f(P,Q+1) laluan untuk mendapatkan dari (P,0) hingga (0,Q+1) ialah nombor f(P,Q) laluan untuk mendapatkan dari (P,0) hingga (0,Q), dan kemudian ke (0,Q+1) + nombor f(P-1,Q) laluan untuk mendapatkan dari (P,0) hingga (1,Q), dan kemudian ke (1, Q+1) dan (0,Q+1), dan sebagainya. Formula yang sepadan adalah seperti berikut:\[f(P,Q+1) = f(P,Q) + f(P-1,Q) + f(P-2,Q) + \ldots + f(1,Q) + f(0,Q)\]
- Kami kini akan mengambil formula ini dan menggantikan P dengan P + 1. Jika kita palamkan P + 1 ke dalam formula dan bukannya P, kita akan mendapat yang berikut: \[f(P+1,Q+1) = f(P+1,Q) + f(P,Q) + f(P-1,Q) + \ldots + f(0,Q)\] \[f(P+1,Q+1) = f(P+1,Q) + f(P,Q+1)\]Daripada terbitan baru ini, kita boleh menentukan formula \(f(P,Q) = f(P,Q-1) + f(P-1,Q)\) Mana \(f(P,0) = 1\) dan \(f(0,Q) = 1\).
-
- Selalunya terdapat beberapa cara untuk dikira dalam masalah gabungan. Terbitan berikut akan menyediakan cara yang berbeza dan lebih elegan untuk memperoleh formula.
- Kami akan menggunakan perwakilan yang sama yang kami gunakan sebelum ini, di mana kami ingin mencari jumlah laluan yang membawa kami dari (P,0) hingga (0,Q). Kita boleh mengatur laluan ini kepada dua kumpulan.
- Laluan yang bermula dengan langkah pertama pergi ke kanan dari (P,0) ke (P,1). Kami tahu bahawa dalam kumpulan ini, kami akan mempunyai sejumlah laluan f(P,Q-1) dari (P,1) hingga (0,Q). Kami tahu ini kerana segi empat tepat yang tinggal selepas bergerak satu ke kanan adalah saiz P x (Q-1).
- Kumpulan lain adalah laluan yang bermula dengan langkah pertama naik satu bergerak dari (P,0) ke (P-1,0). Dalam kumpulan ini, kita tahu terdapat jumlah laluan f(P-1,Q), kerana segi empat tepat yang terhasil adalah saiz (P-1) x Q.
- Oleh itu, kerana setiap laluan yang mungkin akan jatuh ke dalam salah satu daripada dua kumpulan ini, jumlah laluan adalah jumlah kumpulan ini. Ini memberi kita formula yang sama \(f(P,Q) = f(P,Q-1) + f(P-1,Q)\).
-
- Daripada memulakan laluan dari sudut kanan bawah, mari kita putar segi empat tepat supaya titik (P,0) berada di bahagian atas. Kita kini boleh menggambarkan laluan dengan gambar rajah berikut:
-
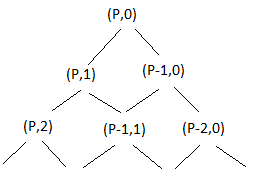
- Gambar rajah jenis ini dikenali sebagai pokok. Corak ini akan terus berulang sehingga kita telah mengembara dari (P,0) hingga (0,Q). Apabila itu berlaku, pokok itu akan mengandungi setiap laluan yang mungkin boleh diambil di seberang papan.
- Bilangan cara untuk pergi dari atas (P,1) ke nod (I,J) di pokok ini adalah bilangan cara untuk sampai ke (I-1,J), dan kemudian turun terus ke (I,J), ditambah dengan bilangan cara untuk sampai ke (I, J-1), dan kemudian turun kiri ke (I,J). Dalam erti kata lain ini adalah nombor dalam Segitiga Pascal.
-
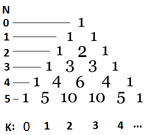
- Setiap nombor dalam Segitiga Pascal adalah jumlah dua nombor di atas. Nombor dalam lajur kiri mengira baris papan, bermula dari 0 dengan papan kosong. Nombor di bawah segitiga mewakili kedudukan dari kiri, juga bermula dari 0. Nombor dalam baris N'th dalam kedudukan K adalah sama dengan \({N \choose K} = \frac{N!}{(N-K)!K!}\).
- Kami ingin mencari nombor f (p, q), yang merupakan bilangan cara untuk mendapatkan dari (P,0) hingga (0,Q). Untuk melakukan itu seseorang perlu pergi dari atas P kali ke kanan dan Q kali ke kiri. Menggunakan struktur pokok yang kita takrifkan sebelum ini, ini sama seperti pergi dari (0,0) hingga (P,Q) hanya pergi kiri dan kanan di pokok itu.
- Walau bagaimanapun, ini menyebabkan kita membuat langkah P + Q, jadi kita berturut-turut P + Q di pokok itu. Oleh kerana kita tahu bahawa kita telah memindahkan Q kali ke kanan, nombor dalam Segitiga Pascal dalam kedudukan ini adalah \({P+Q \choose Q} = \frac{(P+Q)!}{P!Q!}\).
-
- Kami akan menunjukkan bahawa formula berikut adalah setara. \[f(P,Q) = \begin{cases}1 & for & P=0 \\1 & for & Q=0 \\f(P,Q-1) + f(P-1,Q) & for & \text{P>0 and Q>0}\end{cases} = \Bigg\{{P+Q \choose Q} = \frac{(P+Q)!}{P!Q!}\]
- Pangkalan Induksi: Kita sudah tahu bahawa f(0,0) = 1 mengikut definisi formula. Jika kita palamkan P=0 dan Q=0 ke dalam formula, kita akan dapat \(\frac{(0+0)!}{0!0!} = \frac{0!}{1} = 1\). Ini menunjukkan bahawa formula asas adalah bersamaan, yang menyelesaikan asas induksi.
- Hipotesis induksi: Mari kita anggap bahawa formula adalah bersamaan untuk semua nilai P,Q dengan P+Q = N.
- Langkah induksi: Menggunakan hipotesis induksi, kami membuktikan kesetaraan untuk semua nilai P, Q dengan P + Q = N + 1. Untuk sebarang nilai P, Q dengan P + Q = N + 1, kami mempunyai 3 kes:
- Kes 1:
- \(f(N+1,0) = 1\)
- \(f(N+1,0) = \frac{(N+1+0)!}{(N+1)!0!} = \frac{(N+1)!}{(N+1)!} = 1\)
- Kes 2:
- \(f(0,N+1) = 1\)
- Kes ini akan berfungsi sama seperti kes 1.
- Kes 3: \(P,Q > 0\) \[ \begin{align} f(P,Q) &= f(P,Q-1) + f(P-1,Q)\qquad\qquad (+)\\ &= \frac{(P+Q-1)!}{P!(Q-1)!} + \frac{(P-1+Q)!}{(P-1)!Q!}\\ &= \frac{(P+Q-1)!Q}{P!(Q-1)!Q} + \frac{(P-1+Q)!P}{(P-1)!PQ!}\\ &= \frac{(P+Q-1)!}{P!Q!} (Q+P)\\ &= \frac{(P+Q)!}{P!Q!} \end{align} \]
- (+): Jika P + Q = N + 1, maka P + Q-1 = N, iaitu dengan hipotesis induksi.
f(P,Q-1) = \(\frac{(P+(Q-1))!}{(P!(Q-1)!)}\), dan begitu juga untuk f(P-1, Q) - Ini menunjukkan bahawa kedua-dua formula untuk f(P,Q) adalah setara.
- Akhir bukti. ∎
-
- Seseorang hanya boleh menggunakan formula yang sama untuk semua kedudukan yang dipasang ke dalam segi empat tepat dengan baris P-1 dan lajur Q-1, iaitu f(P-1,Q-1).
-
- Jika kedudukan mempunyai jubin N, maka pemain 1 mempunyai pilihan N untuk langkah pertama. Mampu bergerak terlebih dahulu memberi kelebihan kepada pemain 1, dan itu bermakna terdapat lebih banyak kedudukan kemenangan daripada kehilangan kedudukan. Dalam item terdahulu, ia ditubuhkan berapa banyak kehilangan kedudukan antara kedudukan dengan 2,3,4 atau 5 jubin. Berikut adalah beberapa nombor yang mengesahkan trend bahawa lebih banyak jubin kedudukan, semakin tinggi kebarangkalian bahawa ia adalah kedudukan yang menang.
-
# jubin # jawatan # kehilangan kedudukan % kehilangan kedudukan 20 627 42 6.69 30 5604 220 3.92 40 37338 1022 2.73 50 204226 4976 2.43 60 966467 20106 2.08 70 4087968 76688 1.87 80 15796476 270142 1.71 90 56634173 897964 1.58 -
 Apakah fungsi 2 argumen '# kedudukan' dan '# kedudukan yang kalah' memberikan kira-kira nilai yang sama untuk setiap baris jadual di atas?
Apakah fungsi 2 argumen '# kedudukan' dan '# kedudukan yang kalah' memberikan kira-kira nilai yang sama untuk setiap baris jadual di atas?
- Jawapannya diberikan dalam item penemuan berikut.
- Terdahulu kami menunjukkan bahawa setiap kedudukan sama ada menang atau kalah. Bukti memberi kita kaedah langsung untuk menentukan langkah demi langkah untuk semua kedudukan sama ada mereka kalah atau menang. Apa yang istimewa ialah kaedah ini tidak memerlukan carian (mencuba bergerak). Ia mengingatkan kita tentang 'Sieve of Eratosthenes' untuk menentukan semua nombor perdana sehingga beberapa saiz.
-
- Untuk mencari semua nombor perdana sehingga saiz N2, di mana N ialah beberapa nombor bulat, seseorang akan melakukan perkara berikut:
- J: Mulakan dengan nombor perdana p = 2.
- B: Menyeberangi semua gandaan p sehingga N2.
- C: Cari nombor terbesar seterusnya > p yang belum diseberang lagi. Jika nombor itu > N, maka algoritma berhenti. Jika tidak, hubungi nombor ini p dan teruskan dengan langkah B.
- Semua nombor sehingga N 2 yang tidak diseberang adalah semua nombor perdana < N2. Seseorang boleh mencari simulasi algoritma ini pada https://en.wikipedia.org/wiki/Sieve_of_Eratosthenes
- Analogi ini memberi inspirasi kepada kita untuk memikirkan lebih banyak persamaan antara nombor perdana dan kehilangan kedudukan. Ia membawa kepada hipotesis untuk kehilangan kedudukan yang serupa dengan 'Teorem Nombor Perdana'. Berikut adalah butirannya.
- Jadual: Analogi antara kehilangan kedudukan dalam chomp dan nombor perdana:
Nombor Chomp Terdapat banyak nombor bulat tak terhingga. Terdapat banyak jawatan Chomp. Terdapat nombor perdana dan nombor yang boleh diambil kira. Terdapat kehilangan kedudukan dan kedudukan yang menang. Terdapat banyak nombor perdana. Terdapat banyak kedudukan yang kalah. Nombor yang boleh difaktorkan ialah produk nombor perdana dan nombor. Kedudukan yang menang adalah jumlah kedudukan yang kalah dan kedudukan (kerana apa yang dipotong dalam langkah mempunyai bentuk tangga, dan oleh itu adalah kedudukan). Sebaik sahaja nombor perdana diketahui, seseorang tahu serta-merta banyak nombor yang boleh difaktorkan (semua gandaan nombor perdana). Sebaik sahaja kedudukan kalah diketahui, seseorang tahu serta-merta banyak kedudukan yang menang (semua kedudukan yang terhasil daripada mengisi segi empat tepat sudut, termasuk yang panjang tanpa had di sepanjang baris atas dan lajur kiri). Sebilangan besar lebih cenderung dapat dibahagikan dengan nombor perdana yang kecil daripada dengan nombor perdana yang besar. Kedudukan yang besar lebih cenderung dikurangkan kepada kedudukan kalah yang kecil daripada kedudukan kalah yang besar. Untuk menentukan sama ada nombor N adalah nombor perdana, sangat berkesan untuk mengetahui semua nombor perdana P sehingga punca kuasa dua N. Kemudian, seseorang boleh menyemak sama ada N boleh dikurangkan kepada P mengikut bahagian, iaitu oleh bahagian percubaan N / P. Untuk menentukan sama ada kedudukan P adalah kedudukan yang kalah, adalah perlu untuk mengetahui semua kehilangan kedudukan L yang terkandung dalam P. Seseorang kemudian boleh menyemak dengan cekap sama ada P boleh dikurangkan kepada L dalam satu langkah. 'Sieve of Eratosthenes' adalah cara yang cekap untuk menentukan semua nombor perdana sehingga beberapa nombor N, tetapi juga untuk memeriksa sama ada nombor yang diberikan adalah nombor perdana. Algoritma ini diterangkan di atas. Begitu juga dengan 'Sieve of Eratosthenes' yang bermula dengan kedudukan kalah {1}, dan melintasi semua kedudukan kemenangan yang berkurangan kepada kedudukan yang kalah dalam satu gerakan. Satu kemudian memeriksa semua kedudukan dengan satu lagi jubin. Semua jawatan yang tidak dilangkau kehilangan kedudukan. Baki ketidakcekapan algoritma penapis terdiri daripada menyebarkan nombor yang boleh difaktorkan berulang kali. Ketidakcekapan algoritma penapis yang tinggal terdiri daripada menyeberangi kedudukan kemenangan berulang kali. Ketumpatan nombor perdana berkurangan dengan saiznya; iaitu nisbah (# nombor perdana sehingga beberapa nombor bulat N) / N berkurangan apabila N meningkat. Ketumpatan kehilangan kedudukan berkurangan dengan saiznya; iaitu nisbah (# kehilangan kedudukan dengan jubin N) / (# semua kedudukan dengan jubin N) berkurangan apabila N meningkat. (Cabaran: Apakah formula untuk pergantungan nisbah ini pada N dan bagaimana ia dibandingkan dengan formula untuk ketumpatan nombor perdana?). Teorem nombor perdana: (# perdana ≤ N) / (N / log(N)) → 1 sebagai N → infiniti. Hipotesis analog: (# kehilangan kedudukan dengan jubin N) / ((# kedudukan dengan jubin N) / log (# kedudukan dengan jubin N)) → 0.283... sebagai N → infiniti. - Jadual: Perbezaan antara kehilangan kedudukan dalam Chomp dan nombor perdana:
Nombor Chomp Set semua nombor bulat adalah set yang dipesan sepenuhnya; iaitu antara dua nombor, seseorang tahu yang mana lebih besar. Set semua kedudukan Chomp adalah set yang sebahagiannya diperintahkan. Jawatan boleh terkandung sepenuhnya dalam jawatan lain, tetapi tidak perlu. Operasi untuk mengurangkan bilangan kepada salah satu faktor utamanya adalah pembahagian. Operasi untuk mengurangkan kedudukan ke kedudukan yang kalah adalah penolakan jubin. Nombor boleh digambarkan sebagai segmen baris pada baris nombor satu dimensi. Kedudukan ditakrifkan melalui senarai nombor yang diisih mengikut saiz dan dengan itu ialah objek 2D. - Soalan Terbuka:
- Adakah hipotesis (# kehilangan kedudukan dengan jubin N) / ((# kedudukan dengan jubin N) / log (# kedudukan dengan jubin N)) → 0.283... sebagai N → infiniti benar?
- Bolehkah anda membuktikannya? (Kita belum boleh :-) )
- Permainan Chomp yang dimainkan di atas adalah versi 2D Chomp. Ini bermakna papan hanya 2 dimensi, mempunyai lebar dan ketinggian.
-
- Cara paling mudah untuk membayangkan menambah dimensi baru pada permainan adalah dengan menambah dimensi ketiga ke papan. Daripada hanya lebar dan ketinggian, papan baru akan mempunyai panjang, lebar dan ketinggian. Jika seseorang mempunyai sedikit kiub untuk dimainkan, seperti dadu, mereka boleh memainkan permainan 3D ini seperti yang ditunjukkan dalam gambar di bawah.
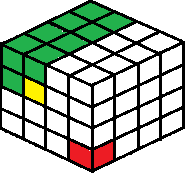
- Apabila bergerak, seseorang akan mengeluarkan kiub yang dipilih, serta setiap kiub ke kiri, di atas dan atas kiub yang dipilih. Langkah sampel diserlahkan dalam warna kuning dalam imej, yang juga menghilangkan semua jubin hijau dalam imej juga. Orang yang mengambil jubin terakhir, yang ditunjukkan oleh jubin merah dalam imej, adalah pemain yang kehilangan permainan.
- Untuk menjadikan bermain permainan lebih mudah dengan kiub sebenar, seseorang boleh menolak kiub ke sudut, seperti sudut kotak kasut, supaya jubin merah berada di sudut kotak, dan hanya boleh diakses sebaik sahaja semua kiub lain telah dikeluarkan juga. Menggunakan kotak ia tidak perlu, tetapi ia akan menstabilkan kiub dan memudahkan untuk mengeluarkan kiub tanpa mengetuk keseluruhan struktur.
-
- Terdahulu kami memutuskan bahawa ia cukup mudah untuk menambah dimensi baru kepada permainan Chomp. Jika seseorang mahu bermain Chomp dalam dimensi yang lebih tinggi daripada 3D, mereka akan terus menambah dimensi baru ke papan Chomp. Walau bagaimanapun, selepas 3D tidak ada cara untuk mensimulasikan papan Chomp menggunakan blok lagi. Walau bagaimanapun, terdapat cara untuk mensimulasikan permainan chomp menggunakan pensil dan kertas, dan kaedah ini membolehkan kita bermain permainan dalam beberapa dimensi, bukan hanya 2D atau 3D.
- Kami akan mulakan dengan bermain permainan 2D Chomp di atas kertas. Cara seseorang boleh mensimulasikan permainan adalah dengan terlebih dahulu memilih nombor yang hanya mempunyai 2 faktor utama yang berbeza. Contohnya, 72 = 2 3 x3 2. Kami kemudian menulis semua faktor nombor ini dalam bentuk segi empat tepat, seperti yang ditunjukkan di bawah.
72 36 18 9 24 12 6 3 8 4 2 1 - Mana-mana nombor jiran yang betul adalah lebih kecil dengan faktor 2 dan mana-mana nombor jiran di bawahnya adalah lebih kecil dengan faktor 3. Untuk bergerak di papan ini, seseorang akan memilih nombor. Anda kemudian akan mengalih keluar nombor itu, bersama-sama dengan mana-mana faktornya. Sesiapa yang mengambil nombor 72 kehilangan permainan.
- Untuk mempunyai segi empat tepat awal yang lebih besar, seseorang boleh mencari nombor yang lebih besar menggunakan formula 2P x 3Q. Dengan menggantikan P dan Q dengan nombor yang lebih besar, seseorang akan mendapat papan yang lebih besar dan lebih besar untuk Chomp 2D.
-
- Untuk memanjangkan versi pensil dan kertas Chomp ini dari 2D ke 3D, seseorang hanya perlu memanjangkan formula yang digunakan untuk mencari nombor permulaan. Daripada memilih nombor yang hanya mempunyai 2 faktor perdana yang berbeza, seseorang akan memilih nombor yang mempunyai 3 faktor perdana yang berbeza. Kita boleh menggunakan formula baru untuk mencari nombor ini seperti berikut: 2P x 3Q x 5R. Kemudian, menggunakan kaedah yang sama seperti sebelum ini, permainan boleh disimulasikan dalam 3 dimensi. Pergi ke dimensi yang lebih besar hanya memerlukan menambah nombor perdana baru ke formula, bergantung kepada bilangan dimensi yang anda mahukan.
- Laman Wikipedia Chomp - https://en.wikipedia.org/wiki/Chomp.
- Permainan Chomp - https://www.win.tue.nl/~aeb/games/chomp.html.
- Permainan Jenis Nim Ingin Tahu - https://www.jstor.org/stable/pdf/2319446.pdf?_=1469549612831.
- Tempoh Poset-Permainan - http://e.math.hr/dvijeigre/byrnes/main.pdf.
- Chomp, Ulangan, dan Kekacauan - http://www.math.rutgers.edu/~zeilberg/mamarim/mamarimPDF/byrnes.pdf.
- Chomp Tiga Baris - http://www.math.rutgers.edu/~zeilberg/mamarim/mamarimPDF/chomp.pdf.
- Penambahbaikan pada Chomp - https://www.emis.de/journals/INTEGERS/papers/cg1/cg1.pdf.
- Sieve laman Wikipedia Eratosthenes - https://en.wikipedia.org/wiki/Sieve_of_Eratosthenes.
- Dan rujukan yang dipetik di halaman ini.





Ikuti atau langgan untuk kemas kini: