Chomp
Total number of plays: 1848453
Total number of wins: 160507
Total number of wins: 160507
How To Play:
- The game is played with two players, either you and a friend, or you against the computer.
- Each player will take turns taking candy from the grid below.
- When a piece of candy is selected, all the pieces below and to the right of that piece are also removed from the board.
How To Win:
- The player who takes the last piece of candy from the top left position loses the game.
No comments at the moment
Player 1's Turn
Access to 'Some food for thought' (SFFT) for the iChomp game can be purchased in the online shop
If you just want to get better in the game as fast as possible then advance to 'More About How to Play' >> 'How to learn losing positions with the computer?'.
The following food for thought varies in difficulty. Some of it is suitable for elementary school students, for example, the item "Let's Try Something Out". Other items demonstrate mathematical proofs and the benefit one may get from them. This is high school material. Please see for yourself what is suitable for you or your Caribou School Math Club.
You get the most out of the activities by first thinking for a while before expanding the answers to the questions.
Have fun.
- A field is the cross-point of a row and column, labelled (row, col).
- A tile is the picture on some fields.
- A position consists of all the fields with tiles.
- Let us start with easy problems, i.e. small positions. To create them we click 'Computer: Off'. If we then click on (2,1) only one row of tiles is left.
-
- By clicking on (1,2) only the tile on (1,1) is left, so you lost.
- Let us then click 'New Game' and on (3,1) and (2,2) to have one tile in row 2 and all of row 1.
-
- By clicking on (1,3) only three tiles are left. Can you see that you have no chance?
- Let's click on 'New Game' and click on (3,1) and (2,3).
-
- Your opponent can click on (1,4). Can you see that you have no chance?
-
- If the top row has one tile more than the 2nd row, then no matter what you do, your opponent can always make a move so that the top row has one more tile than the 2nd row. Then no matter what you do, eventually you will need to pick the (1,1) tile and lose the game.
- If a tile is clicked, all tiles below and to the right are removed as well. This rule has a symmetry; i.e. the whole game has the following symmetry: If we exchange rows and columns then the rule stays the same: all tiles to the right become all tiles below and all tiles below become all tiles to the right of the removed tile. In other words, if we mirror a position along the line going through (1,1) and (2,2) then the new position may look different, but it has the same status. The winning move will also be the same move, only mirrored as well.
-
 The position with 3 tiles in the first row and 2 tiles in the second row is hopeless, as we know. What tiles do the mirrored positions have?
The position with 3 tiles in the first row and 2 tiles in the second row is hopeless, as we know. What tiles do the mirrored positions have?
- After mirroring it has 3 tiles in the left column and 2 tiles in the 2nd column.
-
 We know all hopeless positions having tiles only in the first two rows. What does the symmetry tell us about all hopeless positions with tiles only in the first two columns?
We know all hopeless positions having tiles only in the first two rows. What does the symmetry tell us about all hopeless positions with tiles only in the first two columns?
- Hopeless positions with tiles in the first two columns are those where the first column has one more tile than the second column.
- Here is another position without a chance: Click 'New Game' and on (4,1), (2,2) and (1,4).
-
- You need to make sure that after your move the top row and the first column are again of same length. By repeating this pattern, the opponent will eventually have to take the (1,1) tile and lose.
-
 So, if the first row and first column have the same number of tiles and there are no other tiles then the position is hopeless. Which positions can be changed into such a position?
So, if the first row and first column have the same number of tiles and there are no other tiles then the position is hopeless. Which positions can be changed into such a position?
- If a position has the same number of rows and columns, no matter how many tiles there are anywhere else: a move on (2,2) leaves just the first row and first column of equal length, leaving the opponent no chance. So if a position has the same number of tiles in the top row as in the left column then you play at (2,2) and win the game.
- To play Chomp well, one needs to know about winning and losing positions. A winning position is one where one can enforce a win if one plays optimally, no matter what the other side does. A losing position is one where one has no chance if the other side plays optimally. The following points are what one calls in mathematics a definition. In Chomp, losing and winning positions are defined through these 3 points:
- If only one tile is left (in the top left corner), then this is a losing position.
- A position is a winning position if there exists a move that results in a losing position for the opponent.
- A position is a losing position if every move results in a winning position for the opponent.
- At first glance the above points may look useless because winning positions are explained by losing positions, and losing positions are explained by winning positions. Nevertheless, the definition is based on performing moves, and every sequence of moves does eventually lead to the single tile position which according to point 1 is a losing position.
-
- We will formulate a small theorem and prove it. The proof will show us the way how to reach perfect playing strength. The proof is a proof by induction where one shows that the statement which we want to prove is true for one tile and then show that if it is true for any number N of tiles then it must also be true for one more tile, i.e. N+1 tiles. Since this statement is true for N=1 tile, it must be true for N+1=1+1=2 tiles. But being true for N=2, it then must also be true for N+1=2+1=3 tiles, and so on; i.e. for any number of tiles.
- Lemma (small theorem): Each position is either a winning or a losing position.
- Proof by induction:
- Induction Base: If the position has only one tile then this tile is in the top left corner and then the position is a losing position according to the rule of Chomp (showing that the lemma is true if only N=1 tile is present).
- Induction hypothesis: We assume the lemma is true for all positions with up to N tiles, i.e. positions with 1,2,..., N tiles are either winning or losing positions.
- Induction step: We now want to show that then also all positions with N+1 tiles must be either losing or winning positions.
- In the following P is an arbitrary position with N+1 tiles. If P is reduced by one move then the new position must have ≤N tiles, so it is a losing or a winning position according to induction hypothesis. If P can be reduced in one move to a losing position then P is a winning position. If not, then P can be reduced in one move only to a winning position. But if a position can be reduced in on move only to a winning position then P must be a losing position. This proves that P (having N+1 tiles) is either a winning or a losing position. This shows that all positions (with N+2,N+3,... tiles) are either winning or losing positions.
End of Proof ∎ - Additional Comment: The induction step provides a method to decide for all positions (up to some size) whether they are winning or losing positions. It is defined by the following:
One starts with N=1 and labels that position as a losing position. One then determines the status of all positions with 2 tiles, then with 3 tiles and so on, each time using the knowledge of the status of the smaller positions, and adding the newly found losing position to the list of known losing positions. - This is a very efficient way to find all winning and losing positions up to some size. As the numbers get larger in size, a computer program would be helpful. Necessary ingredients are as follows:
- A procedure that can efficiently create all positions of N tiles from knowing all positions of less than N tiles
- A procedure that can efficiently check whether or not a position can be reduced to another given position.
-
- There are only two possible positions that have exactly 2 tiles, 2 tiles in the top row, or two tiles along the left column. Both of these positions are winning positions.
-
- There are 3 total possible positions that have exactly 3 tiles. They consist of 2 winning positions, and 1 losing positions. Can you figure out which positions they are?
-
- There are 5 possible positions that have exactly 4 tiles. All of these positions are winning positions.
-
- There are 7 total possible positions that have exactly 5 tiles. From these positions, 3 are losing positions and 4 are winning positions. Can you figure out which ones they are?
-
- The following lemma answers this question. The proof is an existence proof. It will only prove the existence of a winning move without showing what the move is. Nevertheless, knowing the lemma is useful for your play as explained below.
- Lemma: All rectangular positions except the 1-tile position are winning positions.
- Proof: To show this is true we need to consider two possible cases:
- Removing the tile in the lower right corner of the board is a winning move.
- Removing the tile in the lower right corner is not a winning move.
- If case 1 is true, then that means that the rectangle is a winning position, and this supports the lemma.
- If case 1 is not true, then we need to consider case 2. According to the proof we did earlier, the position resulting from removing the tile in the lower right corner must then be a winning position, which means it must have a winning move that exists. But, because each move in a rectangle removes the tile in the lower right corner, the losing position resulting from the 2nd move (the winning move) is the same whether the winning move is played after the corner move or instead of the corner move. This means that the winning move could have been played right away, thus proving that a winning move existed for the rectangular position.
- End of Proof ∎
- Additional Comments: Although the lemma does not tell us what the winning move is, it already is helpful to know that rectangular positions are winning positions. One therefore should not make a move that creates a rectangular position (except the 1x1 position).
-
- For all squares of size >1 the only winning move is on (2,2).
-
- The move (2,2) is also a winning move for any position where the 1st row and 1st column have same length.
-
- Yes a position can have more then one winning move. Consider the following position:
###
##
#
This board position has 3 different winning moves that can be made. Can you determine what they are?
- Yes a position can have more then one winning move. Consider the following position:
- The general strategy for winning at Chomp is to create losing positions for your opponent so that they have no chance. We also want to avoid creating winning positions that the opponent can turn back into losing positions for us.
- The key to winning is to know as many losing positions as possible, and to detect how to create one before your opponent does. Let's consider the following possible board, which is a known losing position:
#######
###
###
#
#
- Figure 1
-
- The above losing position can result from any move marked with a + below:
Figure 2 These moves are all situated in the cut out corners. Any such + move will also cut out tiles that may appear in the images below with ?:#######+
###
###
#
########
###+
###
#
########
###
###
#+
########
###
###
#
#
+ -
Figure 3#######+?
###
###
#
########
###+???
###????
#
########
###
###
#+?
#??#######
###
###
#
#
+
? - The + tiles are necessary, and the ? tiles are optional. In the left winning position, the top row can be extended arbitrarily to the right with more '?', and in the right winning position, the first column can be extended arbitrarily to the bottom with more '?'. All of these positions are also winning positions. If we are to make a move in such a position, we will take a + tile, and therefore all the ? tiles connected will also be removed, resulting in the losing position we started with.
- The above losing position can result from any move marked with a + below:
-
- For each losing position there are infinitely many positions which can be turned into this losing position by a single move. All of those infinitely many positions are therefore winning positions.
- Any position has at least 2 corners. The losing position in Figure 1 has 4 corners which are the places where a + is shown in Figure 2. Any position which has a # at the + and possibly #'s to the right of the + and/or underneath the + (where currently ? are shown in Figure 3), all of them would be converted to the losing position when + is clicked.
- In the position with the + in the top row (left-most diagram in Figure 3) can be 0, 1, 2, 3, ... many # to its right. All of these infinitely many positions would be turned into the single losing position by clicking +. Similarly, in the right-most diagram of Figure 3, underneath + there can be arbitrarily many double-crosses and all of these infinitely many positions are turned into the single losing position by clicking the +
- Therefore, there are a lot more winning positions than losing positions. Therefore, it is most effective to remember as many losing positions as possible, all other positions are winning positions.
-
 Make a list of losing positions that you know, and for each position write down all the corresponding winning positions and how to detect them
Make a list of losing positions that you know, and for each position write down all the corresponding winning positions and how to detect them
- The following example shows what we mean:
- As shown earlier, when the position has only 2 rows, and the top row has one tile more than the second row, than this is a losing position, as shown below:
- #####
#### - Taking this known losing position, we can determine that the corresponding winning positions are:
-
#####+?
#########
####+#####
####
+???
???? - In the left position, there can be any number of ? to the right of the top row, and in the right position, there can be any number of rows of ? underneath. We can summarize in words how to detect these winning positions (which you should remember for your play):
-
- A position is a winning position that reduces to
#####
#### - - If either the position has only two rows, and the first row is not exactly one tile longer then the second row, or
- - If the position has more than two rows, and the first row is exactly one tile longer then the second row.
- A position is a winning position that reduces to
- But there is more to think about as well. We not only want to play correctly in such winning positions, we also want to avoid making a move that creates such winning positions. This means that we should not make a move where only two rows remain, or where the second row has exactly one tile less then the first row.
- To summarize, we want to create losing positions, but we also want to avoid creating positions which are one move away from a losing position.
- Another thing to note: due to the mirror symmetry mentioned earlier, all the above comments can be repeated by simply replacing the word "row" with the word "column".
- It is left to you to collect more losing positions and their corresponding winning positions which are one move away.
-
- If you realize that you have to make a move in a losing position, then in theory you have no chance. All you can do is hope that your opponent does not know all winning moves for the positions that you can create with your next move. What you could do is only remove a single tile from a corner. This gives your opponent a resulting position of maximal size, and it makes it more difficult for your opponent to know the corresponding winning move.
-
- One would have to perform what is known as a complete tree search. The first player starts by guessing a move, then the second player guesses a move and so on until one player, say player A, wins. Then player B is allowed to change the last move they made and it is player A's turn next. If in one position the player playing next, say B, runs out of moves because all moves lead to a loss, then this is a losing position, and player B can change the last move made before this losing position was reached.
- This 'tree search' continues until it is clear whether the starting position is a losing position or which move of player 1 turns it into a losing position.
- This can be a very lengthy process if one tries to do it on an initial board with many tiles. However, the more losing positions we know the shorter the sequences of moves are before such a position is reached, and thus the whole search is much faster. If we knew all contained losing positions, then either the starting position would be recognized as a losing position, or only one move would be necessary to reduce it to a losing position.
-
- In the difficulty level 'Very Hard' and positions not bigger than 8 x 15 the computer plays perfectly so each position that results from a computer move is a losing postion! One should start with very small boards and play against the computer in the 'Very Hard' level and learn all the positions that the computer generates. For each such position think of how each one of your moves would be answered by the computer turning it again into a smaller losing position. For each losing position also the mirrored position (rows <--> columns) is a losing position.
-
- In the contest the starting position will be a rectangle of candies. As proven earlier, a rectangle is a winning position, but what is the first move changing it into a losing position for the opponent? We learned earlier that the optimal move for a square is the (2,2) tile but what if the rectangle is not a square?
- Simply change to the 'very hard' difficulty level and let the computer make the first move. As long as the rectangle is not bigger than 8x15, the computer plays optimally and will show the perfect first move. Try different rectangle sizes and remember the optimal first move because the computer play will not be available on contest days :).
- Soon you will be unbeatable in easy and medium difficulty level.
-
- We already met these two families of losing positions. N is any positive integer.
- N tiles in the 1st (left) column and N tiles in the 1st (top) row,
- N tiles in the 1st row and N-1 tiles in the 2nd row including its mirrored version with row <--> column.
- Here are more:
- 3+2N tiles in 1st row, 2+2N tiles in 1st column, 1 tile at (2,2), N>=0,
- 3+2N tiles in the 1st column, 3 tiles in the 2nd column, 4+2N tiles in the 1st row,
- 6+2N tiles in the 1st column, 3 tiles in the 2nd column, 5+2N tiles in the 1st row,
- plus their mirrored (row <--> column) versions.
- The computer player built into the game uses different techniques for different playing levels.
-
- Easy - Makes random moves each turn. If a simple winning position is detected, it will move there.
- Medium - Still moves randomly, but has a greater knowledge of winning and losing positions. Will avoid moves that give the opponent access to a simple winning move.
- Hard - Has an even larger knowledge of winning positions. Actively searches the board for moves that can force the opponent to make a losing move themselves.
- Very Hard - Will always make the optimal move for any position that fits into an 8x15 size rectangle.
- The higher the difficulty level, the harder it will be to force the computer into a losing position. Each level knows many more winning and losing positions than the previous level, and the harder the difficulty, the more winning and losing positions you will need to know to try and force the computer into a losing position.
- The following comments will not help to get stronger in Chomp, but they will provide some interesting facts and give us another opportunity for practising proofs by induction.
-
 How many different positions, including the empty board, fit into a rectangle with P rows and Q columns?
How many different positions, including the empty board, fit into a rectangle with P rows and Q columns?
- If we include the empty rectangle, we can calculate the total number of positions possible using the following formula: \[\frac{(P+Q)!}{P!Q!}\]Can you compute that number for a small P and Q, and verify that it is correct?
-
- Let f(P,Q) be the number of positions in a rectangle of size PxQ. An important observation is that all positions have the shape of a staircase, where each row has at most as many tiles as the row above, but not more.
- Lets first start with a way we can represent all of these staircases. One way to easily create a staircase is to start at the bottom left corner of the board, and either move right or up. One can keep making these right and up moves until they get to the top right corner of the board. We will refer to this as a path that we took to get from (P,0) to (0,Q).
- The number of positions is the same as the number of paths from (P,0) to (0,Q), as long as one is only allowed to move up or to the right. The number f(P,Q+1) of paths to get from (P,0) to (0,Q+1) is the number f(P,Q) of paths to get from (P,0) to (0,Q), and then to (0,Q+1) + the number f(P-1,Q) of paths to get from (P,0) to (1,Q), and then to (1,Q+1) and (0,Q+1), and so on. The corresponding formula is as follows:\[f(P,Q+1) = f(P,Q) + f(P-1,Q) + f(P-2,Q) + \ldots + f(1,Q) + f(0,Q)\]
- We will now take this formula and replace P with P + 1. If we plug P + 1 into the formula instead of P, we get the following: \[f(P+1,Q+1) = f(P+1,Q) + f(P,Q) + f(P-1,Q) + \ldots + f(0,Q)\] \[f(P+1,Q+1) = f(P+1,Q) + f(P,Q+1)\]From this new derivation, we can determine the formula \(f(P,Q) = f(P,Q-1) + f(P-1,Q)\) where \(f(P,0) = 1\) and \(f(0,Q) = 1\).
-
- There are often several ways to count in combinatorial problems. The following derivation will provide a different and more elegant way to derive the formula.
- We will use the same representation that we used before, where we want to find the total numbers of paths that take us from (P,0) to (0,Q). We can organize these paths into two groups.
- Paths that start with the first move going to the right from (P,0) to (P,1). We know that in this group, we will have a total of f(P,Q-1) paths from (P,1) to (0,Q). We know this because the remaining rectangle after moving one to the right is of size P x (Q-1).
- The other group is paths that start with the first move going up one move from (P,0) to (P-1,0). In this group, we know there are f(P-1,Q) total paths, since the resulting rectangle will be of size (P-1) x Q.
- Therefore, since every possible path will fall into one of these two groups, the total number of paths is the sum of these groups. This gives us the same formula \(f(P,Q) = f(P,Q-1) + f(P-1,Q)\).
-
- Instead of starting out paths from the bottom right corner, let's rotate the rectangle so that the point (P,0) is at the top. We can now visualize the paths by the following diagram:
-
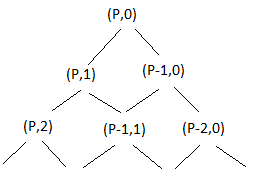
- This type of diagram is known as a tree. This pattern will keep on repeating until we have travelled from (P,0) to (0,Q). When that happens, the tree will contain every possible path one can take across the board.
- The number of ways to get from the top (P,1) to a node (I,J) in this tree is the number of ways to get to (I-1,J), and then going down right to (I,J), plus the number of ways to get to(I,J-1), and then going down left to (I,J). In other words this is the number in Pascal's Triangle.
-
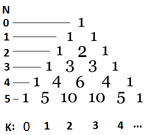
- Each number in Pascal's Triangle is the sum of the two numbers above. The numbers in the left column are counting the rows of the board, starting from 0 with an empty board. The numbers below the triangle represent the position from the left, also starting from 0. The number in the N'th row in position K is equal to \({N \choose K} = \frac{N!}{(N-K)!K!}\).
- We want to find the number f(p,q), which is the number of ways to get from (P,0) to (0,Q). To do that one has to go from the top P times down right and Q times down left. Using the tree structure we defined earlier, this is the same as going from (0,0) to (P,Q) going only left and right in the tree.
- However, this causes us to make P+Q steps, so we are in row P+Q in the tree. Since we know that we have moved Q times to the right, the number in Pascal's Triangle in this position is \({P+Q \choose Q} = \frac{(P+Q)!}{P!Q!}\).
-
- We are going to show that the following formulas are equivalent. \[f(P,Q) = \begin{cases}1 & for & P=0 \\1 & for & Q=0 \\f(P,Q-1) + f(P-1,Q) & for & \text{P>0 and Q>0}\end{cases} = \Bigg\{{P+Q \choose Q} = \frac{(P+Q)!}{P!Q!}\]
- Induction Base: We already know that f(0,0) = 1 by the formula definition. If we plug P=0 and Q=0 into the formula, we get \(\frac{(0+0)!}{0!0!} = \frac{0!}{1} = 1\). This shows that the base formulas are equivalent, which finishes the induction base.
- Induction Hypothesis: Let's assume that the formulas are equivalent for all values of P,Q with P+Q = N.
- Induction Step: Using the induction hypothesis, we prove equivalence for all values P,Q with P+Q=N+1. For any values P,Q with P+Q=N+1, we have 3 cases:
- Case 1:
- \(f(N+1,0) = 1\)
- \(f(N+1,0) = \frac{(N+1+0)!}{(N+1)!0!} = \frac{(N+1)!}{(N+1)!} = 1\)
- Case 2:
- \(f(0,N+1) = 1\)
- This case will work the same as case 1.
- Case 3: \(P,Q > 0\) \[ \begin{align} f(P,Q) &= f(P,Q-1) + f(P-1,Q)\qquad\qquad (+)\\ &= \frac{(P+Q-1)!}{P!(Q-1)!} + \frac{(P-1+Q)!}{(P-1)!Q!}\\ &= \frac{(P+Q-1)!Q}{P!(Q-1)!Q} + \frac{(P-1+Q)!P}{(P-1)!PQ!}\\ &= \frac{(P+Q-1)!}{P!Q!} (Q+P)\\ &= \frac{(P+Q)!}{P!Q!} \end{align} \]
- (+): If P + Q = N + 1, then P + Q-1 = N, i.e. by induction hypothesis.
f(P,Q-1) = \(\frac{(P+(Q-1))!}{(P!(Q-1)!)}\), and similarly for f(P-1, Q) - This shows that the two formulas for f(P,Q) are equivalent.
- End of proof. ∎
-
- One can simply use the same formula for all positions fitting into a rectangle with P-1 rows and Q-1 columns, which is f(P-1,Q-1).
-
- If a position has N tiles, then player 1 has N options for the first move. Being able to move first gives player 1 an advantage, and that should mean that there are more winning positions than losing positions. In an earlier item it was established how many losing positions are among the positions with 2,3,4 or 5 tiles. Here are some numbers which confirm the trend that the more tiles a position has, the higher the probability that it is a winning position.
-
# of tiles # of positions # of losing positions % of losing positions 20 627 42 6.69 30 5604 220 3.92 40 37338 1022 2.73 50 204226 4976 2.43 60 966467 20106 2.08 70 4087968 76688 1.87 80 15796476 270142 1.71 90 56634173 897964 1.58 -
 What function of the 2 arguments '# of positions' and '# of losing positions' gives roughly the same value for each row of the above table?
What function of the 2 arguments '# of positions' and '# of losing positions' gives roughly the same value for each row of the above table?
- The answer is given in the following discovery item.
- Earlier we showed that each position is either a winning or a losing position. The proof gave us a direct method to determine step by step for all positions whether they are losing or winning. What was special is that this method did not need any search (trying out moves). It reminded us of the 'Sieve of Eratosthenes' to determine all prime numbers up to some size.
-
- To find all prime numbers up to size N2, where N is some whole number, one would do the following:
- A: Start with the prime number p=2.
- B: Cross out all multiples of p up to N2.
- C: Find the next biggest number > p that is not crossed out yet. If that number is > N, then the algorithm stops. Otherwise, call this number p and continue with step B.
- All numbers up to N2 that are not crossed out are all prime numbers < N2. One can find a simulation of this algorithm on https://en.wikipedia.org/wiki/Sieve_of_Eratosthenes
- This analogy inspired us to think of more similarities between prime numbers and losing positions. It led to a hypothesis for losing positions that is similar to the 'Prime Number Theorem'. Here are the details.
- Table: Analogies between losing positions in chomp and prime numbers:
Numbers Chomp There are infinitely many whole numbers. There are infinitely many Chomp positions. There are prime numbers and factorizable numbers. There are losing positions and winning positions. There are infinitely many prime numbers. There are infinitely many losing positions. A factorizable number is the product of a prime number and a number. A winning position is the sum of a losing position and a position (because what is cut out in a move has the shape of a staircase, and therefore is a position). Once a prime number is known, one knows instantly infinitely many factorizable numbers (all multiples of the prime number). Once a losing position is known, one knows instantly infinitely many winning positions (all positions resulting from filling corner rectangles, including those infinitely long ones along the top row and left column). A large number is much more likely to be divisible by a small prime number than by a large prime number. A large position is much more likely to be reducible to a small losing position than to a large losing position. To determine whether a number N is a prime number, it is very efficient to know all prime numbers P up to the square root of N. Then, one can check whether N can be reduced to P by division, i.e. by a trial division N / P. To determine whether a position P is a losing position, it is necessary to know all losing positions L that are contained in P. One can then efficiently check whether P can be reduced to L in one move. The 'Sieve of Eratosthenes' is an efficient way to determine all prime numbers up to some number N, but also to check whether a given number is a prime number. This algorithm is described above. Similarly to the 'Sieve of Eratosthenes' one starts with the losing position {1}, and crosses out all winning positions that reduce to that losing position in one move. One then inspects all positions with one more tile. All positions that are not crossed out are losing positions. The remaining inefficiency of the sieve algorithm consists of crossing out factorizable numbers repeatedly. The remaining inefficiency of the sieve algorithm consists with crossing out winning positions repeatedly. The density of prime numbers decreases with their size; i.e. the ratio (# of prime numbers up to some whole number N) / N decreases as N increases. The density of losing positions decreases with their size; i.e. the ratio (# of losing positions with up to N tiles) / (# of all positions with N tiles) decreases as N increases. (Challenge: What is the formula for the dependence of this ratio on N and how does that compare to the formula for the density of prime numbers?). Prime number theorem: (# of primes ≤ N) / (N / log(N)) → 1 as N → infinity. Analogous hypothesis: (# of losing positions with N tiles) / ((# of positions with N tiles) / log(# of positions with N tiles)) → 0.283... as N → infinity. - Table: Differences between losing positions in Chomp and prime numbers:
Numbers Chomp The set of all whole numbers is a completely ordered set; i.e. between any two numbers, one knows which is bigger. The set of all Chomp positions is a partially ordered set. Positions can be completely contained in other positions, but need not. The operation to reduce a number to one of its prime factors is division. The operation to reduce a position to a losing position is subtraction of tiles. A number can be visualized as a line segment on a one dimensional number line. A position is defined through a list of numbers sorted by size and thus is a 2D object. - Open Questions:
- Is the hypothesis (# of losing positions with N tiles) / ((# of positions with N tiles) / log(# of positions with N tiles)) → 0.283... as N → infinity true?
- Can you prove it? (We can't yet :-) )
- The Chomp game played above is a version of 2D Chomp. This means that the board is only 2 dimensional, having a width and a height.
-
- The simplest way to imagine adding a new dimension to the game is by adding a third dimension to the board. Instead of just a width and a height, the new board would have a length, a width and a height. If one had little cubes to play with, such as dice, they could play this 3D game as shown in the picture below.
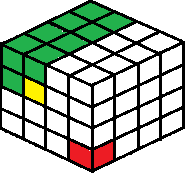
- When making a move, one would remove the cube selected, as well as every cube to the left, above and top of the selected cube. A sample move is highlighted in yellow in the image, which also removes all the green tiles in the image as well. The person who takes the last tile, shown by the red tile in the image, is the player that loses the game.
- To make playing the game easier with real cubes, one can push the cubes against a corner, such as the corner of a shoebox, so that the red tile is in the very corner of the box, and is only accessible once all the other cubes have been removed as well. Using a box it not necessary, but it would stabilize the cubes and make it easier to remove cube without knocking the whole structure over.
-
- Earlier we determined that it is easy enough to add a new dimension to a Chomp game. If one wanted to play Chomp in an even higher dimension than 3D, they would continue to add new dimensions to the Chomp board. However, after 3D there is no way to simulate a Chomp board using blocks any more. There is however a way to simulate the game of chomp using pencil and paper, and this method allows us to play the game in any number of dimensions, not just 2D or 3D.
- We will start by playing a game of 2D Chomp on paper. A way one can simulate the game is by first selecting a number that has only 2 different prime factors. For example, 72 = 23 x 32. We then write down all the factors of this number in the form of a rectangle, as shown below.
72 36 18 9 24 12 6 3 8 4 2 1 - Any right neighbouring number is smaller by a factor of 2 and any neighbouring number underneath is smaller by a factor of 3. To make a move on this board, one would select a number. You would then remove that number, along with any of its factors. Whoever takes the number 72 loses the game.
- To have a larger initial rectangle, one could find a larger number by using the formula 2P x 3Q. By substituting P and Q with larger numbers, one would get larger and larger boards for 2D Chomp.
-
- To extend this pencil and paper version of Chomp from 2D to 3D, one simply needs to extend the formula used to find the starting number. Instead of selecting a number that has only 2 different prime factors, one would select a number that has 3 different prime factors. We can use a new formula to find this number that is as follows: 2P x 3Q x 5R. Then, using the same methods as before, the game can be simulated in 3 dimensions. Going to even larger dimensions simply requires adding new prime numbers to the formula, depending on the number of dimensions you want.
- Chomp Wikipedia page - https://en.wikipedia.org/wiki/Chomp.
- The Game of Chomp - https://www.win.tue.nl/~aeb/games/chomp.html.
- A Curious Nim Type Game - https://www.jstor.org/stable/pdf/2319446.pdf?_=1469549612831.
- Poset-Game Periodicity - http://e.math.hr/dvijeigre/byrnes/main.pdf.
- Chomp, Recurrences, and Chaos - http://www.math.rutgers.edu/~zeilberg/mamarim/mamarimPDF/byrnes.pdf.
- Three-Rowed Chomp - http://www.math.rutgers.edu/~zeilberg/mamarim/mamarimPDF/chomp.pdf.
- Improvements on Chomp - https://www.emis.de/journals/INTEGERS/papers/cg1/cg1.pdf.
- Sieve of Eratosthenes Wikipedia page - https://en.wikipedia.org/wiki/Sieve_of_Eratosthenes.
- And references cited on these pages.





Follow or subscribe for updates: