Фруктовий салат©
Total number of wins: 134290
Як виграти: Перемістіть кожну шторку з правої дошки на один квадрант лівої дошки так, щоб єдині видимі фрукти збігалися з тими, що зображені над дошкою.
Як грати: Натисніть на штору на правій дошці, щоб вибрати її. Після вибору ви можете перемістити шторку, перетягнувши її мишею або сенсорним екраном, а також натискати кнопки під дошкою, щоб перевернути або повернути його. Якщо ви вважаєте, що знайшли рішення, натисніть «Надіслати», щоб перевірити свою відповідь.
Примітка Натомість ви можете використовувати елементи керування клавіатурою (натисніть "Показати елементи керування клавіатурою", щоб відобразити їх). Якщо ви вважаєте, що анімація відволікає, натисніть «Вимкнути анімацію».
| Клавіша зі стрілкою W або UP: Переміщення вибраного штора вгору. | Клавіша зі стрілкою S або ВНИЗ: Переміщення вибраною штору вниз. |
| Клавіша зі стрілкою A або LEFT: Переміщення вибраного штора вліво. | Клавіша зі стрілкою D або RIGHT: Переміщення вибраного штора вправо. |
| Q: Проверніть вибрану штору проти годинникової стрілки. | E: Поверніть вибраний штор за годинниковою стрілкою. |
| F: Переверніть вибрану шторку. | R: Скиньте налаштування плати. |
| Входити: Надішліть свою відповідь. | T: Перехід до наступною штору. |



- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
Ви отримуєте максимальну віддачу від діяльності, спочатку подумавши деякий час, перш ніж розширити відповіді на запитання. Розважатися.
-
У цьому розділі «перевірка штори» означає, коли ви кладете штори десь на дошці і обертаєте/перевертаєте її через усі орієнтації. Слідкуйте за тим, що кожен раз видно, і перевіряйте, чи входять ці фрукти до складу розчину.
- Підказка #1: Знайдіть розділи, куди може потрапити конкретну штору. Зробити це можна, перевіривши однакові штори в кожній секції дошки.
- Підказка #2: Знайдіть те, які штори можуть йти в певному розділі. Це можна зробити, вибравши секцію і перевіривши кожну штори в цьому розділі.
- Підказка #3: Визначте кількість порожніх квадратів, показаних у рішенні. Загальна кількість квадратів, які видно на дошці в будь-який момент часу, дорівнює загальній кількості «отворів» у кожній шторці. В даному випадку виходить 3 + 3 + 3 + 4 = 13 отворів. Щоб знайти загальну кількість видимих порожніх квадратів, відніміть кількість фруктів, які потрібно показати, із загальної кількості видимих квадратів (13). Можна думати про заготовки як про окремий вид фруктів і заповнювати ними ряд видимих фруктів над дошкою, поки не вийде 13.
- Підказка #4: Підрахуйте кількість кожного виду фруктів, які з'являються в питанні. Якщо фрукт взагалі не фігурує в питанні, то це означає, що кожен плід цього типу потрібно покрити. Також слід порахувати кількість кожного виду фруктів, які з'являються на дошці. Це допоможе в разі, якщо кожен однотипний плід потрібно залишити видимим.
- Підказка #5: Почніть зі спроби з'ясувати, куди повинна йти фіолетова штора. Оскільки фіолетова штора єдина, у якої відкритий центр, з'ясувати, куди вона може зайти на дошці, простіше, так як завжди буде видно середній плід її ділянки. Також непогано розмістити зелену штору останньою. Оскільки він має вісім станів (як описано нижче), це може заощадити вам деякий час, якщо ви почекаєте, щоб поставити цу штору до кінця.
- Підказка #6: Використовуйте одну підказку, щоб увімкнути іншу. Навіть якщо підказка не має успіху в розміщенні штори, це може зменшити кількість плодів, які може залишити інша штора. Прикладом цього є те, що питання вимагає, щоб було видно одне яблуко, а конкретна штора завжди розкриває одне яблуко. Це означає, що ніякі інші штори не повинні показувати яблуко, що полегшує розміщення інших штор. Це схоже на гру судоку, де може існувати якесь правило, яке не виправляє розміщення числа, але може обмежити решту варіантів, так що інше правило тепер успішне.
- Підказка #7: Переверніть тільки зелену шторку. Як описано далі, всі штори, крім зеленого, мають дзеркальну симетрію. Тому можна заощадити час, не намагаючись перевернути ці три дзеркальні симетричні штори. Досить спробувати всі їх обертання.
-
Наступні приклади покажуть, що знання підказок з розділу вище допоможе вам вирішити всі головоломки.
- Перш за все, це питання хоче, щоб у нас було показано лише шість бананів. Використовуючи підказку #4, ми бачимо, що всього на дошці всього шість бананів, і ми знаємо, що всі вони повинні бути видимими. Ми також знаємо, що всі інші види фруктів повинні бути покриті.
- Далі, використовуючи підказку #5, ми можемо побачити, що в центрі верхньої правої частини дошки є банан. Це означає, що фіолетова штора повинна йти сюди, оскільки це єдина штора, яка залишає центр видимим. Ми можемо розмістити тут фіолетову штору і повернути її так, щоб не показувалися інші плоди, а потім рухатися далі.
- Тепер ми можемо подивитися на нижню ліву ділянку дошки. Бананів тут немає, а значить, кожен з фруктів в цій секції повинен бути покритий шторою. Використовуючи підказку #2 з трьома шторами, що залишилися, ми бачимо, що зелена штора є єдиною, яка покриває всі ці плоди.
- Тепер ми можемо використовувати підказку #1 на кожному з двох шторами, що залишилися, починаючи з синьої штори. Зробивши це, ми бачимо, що він повинен йти в нижньому правому розділі, оскільки він ніколи не може показати всі три банани у верхній лівій частині. Потім ми поміщаємо рожеву шторку в останню секцію і обертаємо її, щоб показати всі три банани.
- Давайте почнемо з використання підказки #5, щоб визначити, куди повинна йти фіолетова штора. Оскільки верхня права секція має банан в центрі, а нижня ліва секція дошки має помаранчевий в центрі, фіолетова штора не може йти ні в одну з цих двох секцій. Далі, якщо ми використовуємо підказку #1, ми можемо протестувати фіолетову штору у верхній лівій частині та нижній правій частині. Використовуючи підказку #4, ми бачимо, що завжди є яблуко, яке залишається видимим. Це означає, що ми можемо усунути яблуко з плодів, які потрібно залишити видимими, що спрощує питання.
- Тепер ми можемо використовувати підказку #1, спочатку почнемо з рожевої шторки. Тепер, коли ми знаємо, що не можемо показати яблука, ми виявляємо, що єдине місце, куди ця штора може піти, знаходиться у верхньому правому куті.
- Далі давайте перевіримо синю шторку, використовуючи підказку #1 ще раз. Єдине місце, куди ця штора може піти, знаходиться в нижній лівій частині, оскільки він розкриває або банани, або апельсини в інших двох секціях. Тепер ми бачимо, що видно обидві вишні, і тому поки що можемо усунути їх від питання.
- Тепер нам потрібно розмістити решту дві штори таким чином, щоб усі три виноградини, що залишилися, залишалися видимими. Використовуючи підказку #1, ми можемо почати з зеленої штори і побачити, що вона повинна йти в нижній правій частині. Нарешті, ми можемо розмістити фіолетову штору назад у верхній лівій частині, і ми закінчили.
-
Тепер, коли ви знаєте більше про гру та деякі стратегії вирішення питань, давайте вирішимо головоломку для початківців. Натисніть кнопку нижче, щоб відобразити запитання.
-
Тепер давайте вирішимо питання, пов'язане з більш ніж одним видом фруктів. Натисніть кнопку нижче, щоб відобразити запитання.
- Головоломка стає складнішою, коли є більше видів фруктів, які потрібно залишити нерозкритими. Якщо є невелика різноманітність фруктів, наприклад, якщо б ви шукали тільки банани і виноград, ви можете почати з з'ясування того, які розміщення штор залишають видимими тільки ці. Це допомагає зменшити кількість можливих розміщень, і тому головоломку легше вирішити.
- Якщо різноманітності більше, то складніше звузити місця, куди можна розмістити штори, і тому питання складніше. Ось чому важливо використовувати перераховані вище підказки, особливо при спробі вирішити більш складні питання (див. Складний приклад вище).
- Ще одна річ, яка ускладнює головоломку фруктового салату, - це скільки разів вам потрібно поміняти, обертати або перекидати штори, щоб отримати правильну відповідь. Кожне питання на цій веб-сторінці має унікальну відповідь, а це означає, що всі вони мають свій власний набір ходів, які необхідно виконати, щоб отримати правильну відповідь. Ці переміщення не потрібно робити в якомусь певному порядку, і деякі ходи можна замінити іншими (наприклад, триразове обертання фігури вправо те саме, що обертання її один раз вліво). Питання, які мають більший набір ходів, складніші, оскільки знадобиться більше часу, щоб знайти правильну відповідь.
-
Штора може мати різні типи симетрії, дзеркальної симетрії та / або обертальної симетрії. Штора є дзеркально симетрична, якщо перевертання штори має той самий ефект, що й поворот її певну кількість разів. Штора є обертально симетрична, якщо кожне обертання на 90 градусів залишає штору незміненою.
-
Три штори в цій грі дзеркально симетричні. Рожева і фіолетова штори симетричні по діагоналі, а синя симетрична по горизонталі. Зелена штора не є дзеркально симетричною. Для цієї гри не має значення, де знаходиться вісь симетрії, тому що можна обертати кожну штору.



-
Жоден із штор у цій грі не є обертально симетричним. Штори, які мають таку симетрію (але не використовуються в цій грі), включають пряму лінію або форму «X».

-
Штора з дзеркальною симетрією має лише чотири різні стани для перевірки, тому рожева, синя та фіолетова форми мають по чотири стани. Штора, яка не має дзеркальної симетрії, має вісім різних станів для перевірки. Оскільки зелена штора є єдиною, яка не є симетричною, це єдина штора з вісьмома різними станами. Ви можете перевірити це, спробувавши всі обертання кожної штори за годинниковою стрілкою, а потім перевернувши шторку та повернувши її знову.
-
Коли ви починаєте розміщувати штори на дошці, у вас є 4 різні місця для розміщення першою штору, потім 3 різні місця для іншої, 2 різних місця для третього та одне місце, що залишилося для останньої штори. Це залишає нам 4 × 3 × 2 × 1 = 24 розміщення. Це число також можна назвати 4 факторіальним, або 4!.
Три симетричні штори можна повертати чотирма різними способами, як показано раніше. Це дає нам в цілому (4 × 4 × 4) × (4 × 3 × 2 × 1) = 1536 різних розміщень на даний момент.
Нарешті, оскільки зелену штору можна обертати вісьмома різними способами, ми отримуємо в цілому (8 × 4 × 4 × 4) × (4 × 3 × 2 × 1) = 12288 різних розміщень для штор.
-
Тоді буде в цілому (8 × 8 × 8 × 8) × (4 × 3 × 2 × 1) = 98304 різних розміщення штор.
 Для 'n' штор з симетрією і 'm' штор без симетрії знайдіть формулу для розрахунку кількості можливих розміщень штор.
Для 'n' штор з симетрією і 'm' штор без симетрії знайдіть формулу для розрахунку кількості можливих розміщень штор.
-
Скажімо, ми хочемо знайти загальну суму для дошки з 20 симетричними шторами і 5 асиметричними шторами. Замість того, щоб виписувати 20 4 і 5 8, як ми робили раніше, ми можемо створити формулу для спрощення цього обчислення.
З розділу вище ми знаємо, що кількість станів для симетрично дорівнює 4. Ми також бачимо, що для будь-якої кількості симетричних штор загальна кількість розміщень дорівнює 4 n, де 'n' - кількість симетричних штор.
Аналогічно, ми знаємо, що кількість станів для асиметричної штори дорівнює 8, і ми отримуємо загальне число розміщень рівним 8m, де 'm' - кількість асиметричних штор.
Як і раніше, щоб знайти загальну кількість способів розміщення штор (без урахування обертань) на платі, ми використовуємо s!, де 's' - кількість штор.
Множення їх разом дає нам 4n × 8m × s! = t, де 't' - загальна кількість розміщень штор.
Оскільки 22 = 4 і 23 = 8, формулу можна спростити наступним чином:
4n * 8m = (22)n * (23)m
= (22n) * (23m)
= 22n + 3m
Це дає нам остаточну формулу 22n + 3m × s! = t, де 'n' - кількість симетричних штор, 'm' - кількість асиметричних штор, 's' - загальна кількість штор(яку також можна знайти при n + m), а 't' - загальна кількість розміщень штор. Спробуйте застосувати цю формулу, використовуючи цифри для дошки на цій веб-сторінці (одна асиметрична штора і три симетричні штори).
Тепер, коли ми знаємо, що формула правильна, ми можемо з'ясувати кількість розміщень для дошки, описаних на початку цього розділу, з 20 симетричними і 5 асиметричними шторами.
22n + 3m * 25! = t
22(20) + 3(5) * 25! = t
240 + 15 * 25! = t
255 * 25! = t
5.59 x 1041 = t
(Точна відповідь: 558850238169687388730388679609024512000000, або п'ятсот п'ятдесят вісім дуодециліонів, вісімсот п'ятдесят недецильйонів, двісті тридцять вісім децильйонів, сто шістдесят дев'ять нонілліонів, шістсот вісімдесят сім октильйонів, триста вісімдесят вісім септильйонів, сімсот тридцять секстильйонів, триста вісімдесят вісім квінтильйонів, шістсот сімдесят дев'ять квадрильйонів, шістсот дев'ять трильйонів, двадцять чотири мільярди, п'ятсот дванадцять мільйонів.)
-
Хоча знання того, як знайти кількість розміщень, не допоможе вам вирішити головоломки, це все одно корисно. Поки ми розробляли цю гру, нам потрібно було переконатися, що кожне питання має лише одне рішення. Для цього спочатку потрібно було знайти всі можливі місця розміщення для дошки. Для зберігання цих місць розташування ми використовували масив, який має фіксований розмір. Формулою вище ми скористалися для того, щоб визначити, якого розміру повинен бути масив.
-
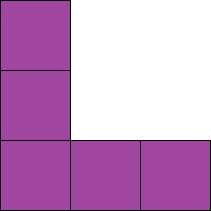
Чотири штори на дошці складаються з менших квадратів. Три з них зроблені з шести квадратів, а інший - з п'яти.
Фігура, яка складається з ряду менших квадратів, називається поліміно. Існують більш конкретні терміни для фігур із певною кількістю квадратів. Гексоміно складаються з шести квадратів, а пентоміно - з п'яти.
Багато відомих ігор використовують поліміно, включаючи Tetris, Blokus і Dominoes. Існують також деякі версії судоку, які використовують поліміно замість квадратів для сітки.
Більше інформації про поліміно можна знайти за адресою:





Слідкуйте за оновленнями або підписуйтесь на них: