Salad trái cây^©

Tổng số người chơi: 389644
Tổng số trận thắng: 133226

Phím mũi tên W hoặc LÊN: Di chuyển rèm đã chọn lên.	Phím mũi tên S hoặc DOWN: Di chuyển rèm đã chọn xuống.
Phím mũi tên A hoặc TRÁI: Di chuyển rèm đã chọn sang trái.	Phím mũi tên D hoặc PHẢI: Di chuyển rèm đã chọn sang phải.
Q: Xoay mù đã chọn ngược chiều kim đồng hồ.	E: Xoay rèm đã chọn theo chiều kim đồng hồ.
F: Lật rèm đã chọn.	R: Đặt lại bảng.
Vào: Gửi câu trả lời của bạn.	T: Đạp xe đến người mù tiếp theo.

Câu hỏi trung gian:

Câu hỏi của chuyên gia:

Bạn tận dụng tối đa các hoạt động bằng cách suy nghĩ một lúc trước khi mở rộng câu trả lời cho các câu hỏi. Chúc vui vẻ.

Một số chiến lược để sử dụng khi giải câu đố Salad trái cây là gì?

Gợi ý # 1: Tìm các phần mà một người mù cụ thể có thể đi. Điều này có thể được thực hiện bằng cách kiểm tra cùng một người mù trong mỗi phần của bảng.

Gợi ý # 2: Tìm những gì rèm có thể đi trong một phần cụ thể. Điều này có thể được thực hiện bằng cách chọn một phần và kiểm tra từng người mù trong phần này.

Gợi ý #3: Xác định số ô vuông trống được hiển thị trong giải pháp. Tổng số ô vuông có thể nhìn thấy trên bảng bất cứ lúc nào bằng tổng số 'lỗ' trong mỗi mù. Trong trường hợp này, có 3 + 3 + 3 + 4 = 13 lỗ. Để tìm tổng số ô vuông trống có thể nhìn thấy, hãy trừ đi số lượng trái cây phải được hiển thị từ tổng số ô vuông có thể nhìn thấy (13).

Gợi ý #4: Đếm số lượng từng loại trái cây xuất hiện trong câu hỏi. Nếu một loại trái cây hoàn toàn không xuất hiện trong câu hỏi, thì điều này có nghĩa là mọi loại trái cây đó cần phải được che phủ. Bạn cũng nên đếm số lượng từng loại trái cây xuất hiện trên bảng. Điều này sẽ giúp ích trong trường hợp mọi loại trái cây cùng loại cần phải được nhìn thấy.

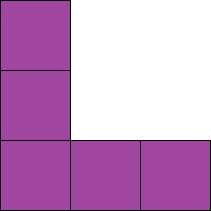
Gợi ý # 5: Bắt đầu bằng cách cố gắng tìm ra nơi người mù màu tím nên đi. Vì rèm tím là người duy nhất có trung tâm mở, việc tìm ra nơi nó có thể đi trên bảng dễ dàng hơn, vì quả giữa của phần của nó sẽ luôn được nhìn thấy. Nó cũng là một ý tưởng tốt để đặt rèm xanh cuối cùng. Vì nó có tám trạng thái (như được mô tả dưới đây), nó có thể giúp bạn tiết kiệm thời gian nếu bạn chờ đợi để đặt rèm này cho đến khi kết thúc.

Gợi ý # 6: Sử dụng một gợi ý để kích hoạt một gợi ý khác. Ngay cả khi một gợi ý không thành công trong việc đặt rèm, nó có thể làm giảm số lượng trái cây có thể bị bỏ lại bởi một người mù khác. Một ví dụ về điều này là nếu một câu hỏi yêu cầu một quả táo được nhìn thấy và một người mù cụ thể luôn tiết lộ một quả táo. Điều này có nghĩa là không có rèm nào khác nên hiển thị một quả táo, điều này giúp người ta dễ dàng đặt các rèm khác hơn. Điều này tương tự như trò chơi Sudoku, nơi có thể có một số quy tắc sẽ không sửa vị trí của một số nhưng có thể giới hạn các tùy chọn còn lại để một quy tắc khác hiện đã thành công.

Hint #7: Flip only the green blind. As described further down, all blinds except the green one have a mirror symmetry. Therefore one can save time by not attempting to flip these three mirror symmetric blinds. Trying all their rotations is enough.

Một số giải pháp có giải thích.

Một câu hỏi dễ

Vui lòng thử và xem bạn có thể đi được bao xa trước khi kiểm tra giải pháp.

Một câu hỏi khó hơn

Vui lòng thử và xem bạn có thể đi được bao xa trước khi kiểm tra giải pháp.

Hãy bắt đầu bằng cách sử dụng Gợi ý # 5 để xác định nơi người mù màu tím nên đi. Vì phần trên cùng bên phải có một quả chuối ở giữa và phần dưới cùng bên trái của bảng có màu cam ở giữa, nên rèm tím không thể đi vào một trong hai phần này. Tiếp theo, nếu chúng ta sử dụng Gợi ý # 1, chúng ta có thể kiểm tra rèm màu tím ở phần trên cùng bên trái và phần dưới cùng bên phải. Sử dụng Gợi ý # 4, chúng ta có thể thấy rằng luôn có một quả táo được nhìn thấy. Điều này có nghĩa là chúng ta có thể loại bỏ táo khỏi các loại trái cây cần được nhìn thấy, điều này giúp đơn giản hóa câu hỏi.

Bây giờ chúng ta có thể sử dụng Gợi ý # 1, chúng ta sẽ bắt đầu với người mù màu hồng trước. Bây giờ chúng tôi biết rằng chúng tôi không thể hiển thị bất kỳ quả táo nào, chúng tôi thấy rằng nơi duy nhất mà người mù này có thể đi là ở phần trên cùng bên phải.

Tiếp theo, hãy kiểm tra rèm xanh, bằng cách sử dụng Gợi ý # 1 một lần nữa. Nơi duy nhất mà người mù này có thể đi là ở phần dưới cùng bên trái, vì nó tiết lộ chuối hoặc cam ở hai phần còn lại. Bây giờ chúng ta có thể thấy rằng cả hai quả anh đào đều có thể nhìn thấy, và vì vậy chúng ta có thể loại bỏ chúng khỏi câu hỏi ngay bây giờ.

Bây giờ, chúng ta cần đặt hai tấm rèm còn lại sao cho cả ba quả nho còn lại đều có thể nhìn thấy được. Sử dụng Gợi ý # 1, chúng ta có thể bắt đầu với rèm màu xanh lá cây và thấy rằng nó phải đi ở phần dưới cùng bên phải. Cuối cùng, chúng ta có thể đặt rèm màu tím trở lại ở phần trên cùng bên trái, và chúng ta đã hoàn tất.

Điều gì làm cho một câu đố Salad trái cây khó hơn?

Có bao nhiêu tấm rèm đối xứng?