Salade de Fruits^©

Nombre total de parties: 389644
Nombre de victoires: 133226

W ou flèche vers le HAUT: Faire déplacer la tuile sélectionnée vers le haut.	S ou flèche vers le BAS: Faire déplacer la tuile sélectionnée vers le bas.
A ou flèche vers la GAUCHE: Faire déplacer la tuile sélectionnée vers la gauche.	D ou flèche vers la DROITE: Faire déplacer la tuile sélectionnée vers la droite.
Q: Faire tourner la tuile sélectionnée dans le sens antihoraire.	E: Faire tourner la tuile sélectionnée dans le sens horaire.
F: Faire retourner la tuile sélectionnée verticalement.	R: Recommencer.
Entrée: Soumettre.	T: Sélectionner la tuile suivante.

Niveau Débutant :

Niveau Intermédiaire :

Niveau Avancé :

Pour en tirer le maximum, il vaut mieux essayer de répondre aux questions par vous-même avant de lire les réponses. Nous espérons que cette discussion vous donnera la banane! :-)

Quelles stratégies adopter pour résoudre un casse-tête « Salade de Fruits »?

Astuce n°1: Identifier les sections où on peut placer une tuile particulière. Pour ce faire, vous pouvez vérifier la tuile dans chaque quadrant de la grille.

Astuce n°2: Identifier quelles tuiles on peut placer sur un quadrant particulier. Pour ce faire, choisissez un quadrant et vérifiez chaque tuile dans ce quadrant.

Astuce n°3: Déterminer le nombre de cases vides visibles dans la solution. Le nombre total de cases visibles sur la grille est toujours égal au nombre de « trous » qu’ont les quatre tuiles. Les tuiles étant toujours les mêmes pour chaque casse-tête, il y aura toujours 3 + 3 + 3 + 4 = 13 trous. Pour déterminer le nombre de cases vides dans la solution, soustrayez le nombre de fruits qui doivent être visibles du nombre total de cases visibles (13). On peut même concevoir que les tuiles sont un autre type de fruit et remplir le nombre de fruits visibles au-dessus de la grille avec ces "fruits" jusqu'à ce qu'il y en a 13.

Astuce n°4: Compter le nombre de chaque fruit figurant dans la question. Si un type de fruit ne figure nulle part dans la question, alors il faut recouvrir chacun de ces fruits dans la grille. Il est utile de savoir qu’il faut laisser découvert chaque fruit d’un certain type, par exemple.

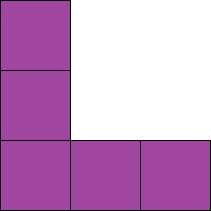
Astuce n°5: Placer la tuile violette en premier. Étant donné que la tuile violette est la seule à avoir la case centrale découverte, c’est la seule dont la case centrale sera visible, et donc son emplacement est le plus facile à trouver. Par ailleurs, il est aussi conseillé de placer la tuile verte en dernier. Puisqu’elle a 8 états (expliqués un peu plus bas), vous pourrez gagner du temps à la placer après les autres.

Astuce n°6: Combiner les astuces pour déterminer un emplacement. Il se peut qu’une seule astuce ne soit pas suffisante pour placer définitivement une tuile. Pourtant, elle peut réduire le nombre de fruits qu’une autre tuile doit laisser découverts. Par exemple, imaginez qu’une question exige qu’une pomme soit visible, et qu’une tuile particulière révèle toujours une pomme. Vous savez alors que les autres tuiles doivent recouvrir toutes les autres pommes. Ceci rappelle un peu le jeu Sudoku, où une règle qui ne force pas le placement d’un chiffre dans une case peut quand même limiter le nombre d’options pour qu’une autre règle puisse réussir à forcer un emplacement.

Astuce n° #7: Ne retourner que la tuile verte. Comme l'on explique ci-dessous, toutes les tuiles excepté la verte ont une symétrie miroir. Alors, on peut gagner du temps en sachant qu'il est inutile de retourner ces trois tuiles symétriques, il suffit donc d'essayer toutes leurs rotations.