Caribou in Covid: Contests are running online as usual. Check out the FAQ for further questions.
300000
59050
Sokoban©
Suggestions on how to play Sokoban
Notation
The following terms will be used throughout this guide:
- move: one step of the worker whether pushing or not pushing a box.
- path: a sequence of moves.
- position: the whole problem with the worker and all boxes being at a certain place.
- solution: a position where each box is sitting on a dot.
- solution path: the sequence of moves from the original position to the solution.
- dead position: a position from which the solution can not be reached.
General Strategy
The shortest solution might contain 100, 300 or even 1000 moves (our simplest game 1 already needs 73 moves, game 8 needs 126 moves). If there are on average, say, 2 possibilities for each move and the solution takes 100 moves then a brute force search would require to search 2100 paths to find the solution. Even for computers this is not possible. We therefore need to:
- recognize early if a position is dead,
- break down the overall goal into sub tasks. If a solution path of 100 moves can be broken down into, say, 10 sub tasks then the complexity of the problem is drastically reduced. Furthermore it might be possible to deduce the order in which the sub tasks need to be completed and then the whole problem becomes easy to solve,
- find restrictions on the solution path,
- think about other heuristics.
About 1) Recognizing dead positions early
1.1) Sometimes it is easy to decide whether a position is dead, one only has to look at the neighbourhood of one single box. All it takes is a 'local' inspection. If a box does not stand on a dot and can not be moved horizontally and not vertically, then the position is dead. The box may be blocked by the wall or by other boxes which also can not be moved.
Examples:
1.2) It is slightly harder to see that a position is dead if the box is next to a wall and it can be pushed but only along the wall on the same side and none of the places it can reach is a dot.
Example:
1.3) In this generalization the box is next to a wall and can be moved to a place where it has not the wall on its side (place A below), but that free neighbouring place A can not be reached by the worker after pushing the box next to A.
Example:
These three cases can be decided locally and without moving the worker. Thus they can be checked out in the initial position and one can mark places as forbidden, say, with ! so that a box may never be pushed on such a place.
1.4) In a further generalization the place A can be reached by the worker but only at the price of putting another box at a forbidden place.
Example:
This explanation is recursive[1], i.e. it characterizes a dead position by using the words 'dead position'. Such dead positions are harder to recognize because they can not be detected by local inspection and might need test moves.
About 2) Formulating Sub Tasks
Examples of sub tasks are:
- Move the worker from A to B,
- Move a certain box from A to B
where each of these tasks is to be accomplished without creating a dead position.
Example for (a): How the worker can pass a box to get to A:
→
→
→
→
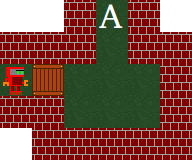All the empty space is needed as the worker has to walk around the box. If there is less empty space then the worker can not pass the box without generating a dead position.
If one knows many such subtasks with their shapes of the corridor by heart then one saves much time by not needing to think about it, here this 9-move-path. More importantly one will not give up because one thinks this sub task is impossible.
A question related to subtasks is how to find them. Subtasks come up, for example, when solving the problem reversely. Suppose a certain dot can only be reached from one side and only by one box. This box consequently needs to be pushed in a particular direction. In order to do so the worker needs to get to the other side of it. A task could be to bring the box and worker in the right position.
Another typical example of coming up with a sub task is the following. It is safe to assume that all interior space in a position is needed for the solution. That means, if the original position has bulky inner spaces, like the 2 times 3 empty area in the above example, then one can ask what is the purpose for that space. It could be that it is needed by the worker to pass a box or it is used to park temporarily a box to free space somewhere else intermediately. So if the bulky space is capable of storing a box temporarily then which box could that be? How can one get this box to this intermediate parking spot?
About 3) Formulating Restrictions on the Solution Path
There are many restrictions on the solution path possible just by looking at the position without trying out moves. Examples are:
3.1) There is a corridor that can be entered by a box but the box can never move through the whole corridor and therefore the space at the end of the corridor can never be reached from the side where the corridor ends.
eg) Point A can never be reached by a box sitting on B and B can not be reached by a box sitting on A by going through the corner.
3.2) A certain dot can be reached only from one side even though there is free space on different sides.
eg) The dot can not be reached by a box from below.
3.3) A certain box can never be moved in a certain direction and therefore can only reach one specific dot.
eg) The box can only reach the dot on its left.
3.4) Because dots can be reached by boxes only from some side it determines the order in which dots must be occupied.
eg) In the following position the left dot has to be occupied before the dot to the right of it.
3.5) It may be clear which point needs to be covered last because the space is needed for the worker to push a box in a certain direction.
eg) The space of the most right dot is needed for the worker to stand and push a box to the left, so the most right dot is the last to be occupied (in the same picture as above).About 4) Other Heuristics
4.1) Any sequence of pushes that can be reversed can and should be tried out, even if it means that the worker has to go a long way in order to push from another side to reverse these pushes. Even if such an exercise looks pointless, the new position may open new possibilities of how to proceed.
4.2) If there is a straight line that separates all dots from at least one box, then this box must cross that line. If this is not possible then the position is dead. If there exists only one way for the box to cross that line then this is a strong restriction for the solution path.
Example of a Complete Solution (Game 8)
(1)
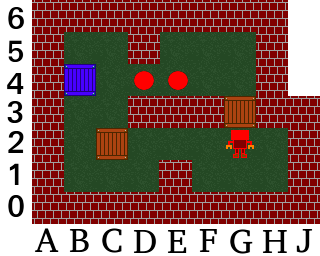
We introduce coordinates to label points. For example, the worker is initially at point G1.
Initially the worker has only the 2 options: a) to go through hole G3, or b) to go through hole E3. Going through G3 does only allow the worker to push the box at B3 to B1 → death. So the worker goes through the hole E3 to B2:
(2)
The only pushes we can make is a) box B3 up to B4 (not to B5 which means death) or box C2 to the right.
We realize that boxes can not be moved to dots on a route through G3 because they could never be moved to the left afterwards (see 1.2).
But in order to move them through the hole B3,C3 we need space in this area, so we need to park one or two boxes on the right and have to get them back afterwards.
We also realize that box B3 can only be moved on the B line and therefore will finally have to end on dot B4.
To move later boxes on C4 and then to push them to the right, the worker must be able to move to A4 but to get there from below, box B3 must be at B2 and spaces B3, C3, C2 must be free, so two boxes must get out of the way and be parked in the lower right.
So, to get box C2 out of the way and get the worker to the left top, we could use example 2.1 and reach
(3)
but pushing down boxes A3 or B3 does not work. The only other option we had in position (2) is to push box B3 up to B4 first and then to do the moves leading to position (3). We get
(4)
Now we can make progress by pushing box C3 down to C2 and move with the worker around to push box F2 to G2 and G3:
(5)
As discussed above, we need spaces B3,C3,C2 free and get box B4 down to B2 so we need to park box C2 temporarily on G2. We get:
(6)
Now we can follow our earlier plan and push box G2 to C4 in order to push it further to the right:
(7)
The question is how far right do we have to push that box C4. Because we still need to push box G3 through the same path we need to get the worker to G4 and to do that we need to push box C4 as far as F4 and move the worker to G4 to push G4 to G3:
(8)
To move box G2 to the left the worker needs to go all the way back counter clockwise to H2.
(9)
The rest is simple: box G2 is pushed to C2, C4, D4
(10)
then box B2 is pushed to B4 and then the worker moves to G4 to finally push box F4 on dot E4.
DONE.
Someone is bankrupt if the person owes someone else money and has no cash money and either has no receipt for having borrowed someone else’s money, or has a receipt for having borrowed someone else’s money but that person is bankrupt.
This explanation of the word bankrupt uses the word bankrupt, and therefore it is called recursive.
Example:
Persons A,B,C have no money, all of them owe some money to person D,
A has a receipt for borrowing money to B,
B has a receipt for borrowing money to C,
C has a receipt for borrowing money to A
but they are as a group bankrupt, each one of them.
Similar but different situation:
Persons A,B,C have no money, all of them owe some money to person D,
A has a receipt for borrowing money to B,
B has a receipt for borrowing money to C,
C has a receipt for borrowing money to F.
Because person F might have money, it may be that none of A,B,C are bankrupt.
To distinguish between the two cases one needs to look at all relations, not only one individually because the above definition of bankruptcy is recursive.
Des Astuces pour Jouer à Sokoban
Notation
Ce guide utilisera les termes suivants :
- coup: un pas du robot, que ce soit une poussée ou un simple déplacement.
- chemin: une séquence de coups.
- position: le puzzle entier décrivant l’emplacement du robot et des boîtes.
- solution: une position où chaque boîte est sur un point rouge
- chemin de solution:la séquence de coups permettant de passer de la position initiale à la solution.
- position morte: une position à partir de laquelle la solution est inatteignable .
Stratégie générale
La solution la plus rapide peut contenir 100, 300, voire 1 000 coups (il faut déjà 73 coups pour compléter notre puzzle le plus simple, dans le 8ème puzzle il faut 126 coups). S’il y a en moyenne deux possibilités pour chaque coup et la solution nécessite 100 coups alors il faudrait chercher 2 100 chemins pour retrouver la solution si on les vérifier un par un. Alors il faut :
- reconnaître les positions mortes au plus tôt,
- diviser l'objectif global en sous-tâches. La complexité du problème est considérablement réduite quand on peut diviser un chemin de solution de 100 coups en 10 sous-tâches par exemple. En plus, il pourrait être possible de déterminer l’ordre dans lequel il faut réaliser les sous-tâches pour faciliter la résolution du problème,
- trouver des restrictions sur le chemin de la solution,
- penser à d'autres heuristiques.
1) 1) Reconnaître les positions mortes au plus tôt
1.1) Parfois il est facile à déterminer qu’une position est morte, il suffit de regarder la région entourant une seule boîte. Une inspection « locale » est suffisante. Si une boîte n’est pas sur un point rouge et ne peut se déplacer horizontalement ni verticalement, la position est morte. La boîte est peut-être bloquée par le mur ou d’autres boîtes qui ne peuvent pas être déplacées non plus.
Exemples:
1.2) Il est un peu plus difficile de voir qu'une position est morte quand la boîte se trouve sur un mur et on peut la pousser mais uniquement le long du même mur où aucune des cases qu’elle peut atteindre n’est un point.
Exemple:
1.3) Dans cette généralisation, la boîte se trouve sur un mur et on peut la déplacer dans une case où elle n’aura pas le mur de côté (la case A ci-dessous), mais le robot ne pourra pas atteindre cette case A car elle sera bloquée par la boîte.
Exemple:
On peut reconnaître ces trois cas localement sans déplacer le robot. Alors on peut les retrouver dès la position initiale pour ensuite les marquer comme « interdits » avec un symbole tel que ! pour éviter de pousser une boîte dans une telle case.
1.4) Prenant cette généralisation plus loin, le robot pourra atteindre la case A mais uniquement s’il condamne une autre boîte.
Exemple:
Cette explication est récursive.[1], c.-à-d. qu’elle définit une position morte en utilisant les mots « position morte ». Il est plus difficile de reconnaître de telles positions mortes car on ne peut pas les détecter localement et il est peut-être nécessaire d’effectuer des coups d’essai.
2) Formuler des sous-tâches
Exemples des sous-tâches:
- Déplacer le robot de A à B,
- Déplacer une boîte de A à B
Où chaque tâche doit être réalisée sans créer de position morte.
Exemple pour (a) : Comment contourner une boîte pour rejoindre la case A:
→→→→
Tout l’espace vide est nécessaire pour que le robot puisse faire le tour de la boîte. Sans cet espace vide le robot ne pourra contourner la boîte sans faire de position morte.
Si on connaît déjà le nombre de sous-tâches ainsi que le plan du labyrinthe, on peut résoudre le problème plus rapidement, dans ce cas-ci le chemin à 9 coups. Encore plus important, on sera plus motivé à compléter la sous-tâche sachant qu’elle n’est pas impossible.
Une question liée à des sous-tâches, c’est comment les identifier, ce qui peut se faire, par exemple, en essayant de résoudre le problème à rebours. Supposons qu’on ne peut atteindre un certain point rouge qu’avec une certaine boîte poussée d’une seule direction. Pour ce faire, le robot doit se mettre dans la case derrière pour pousser la boîte. Une sous-tâche peut consister à mettre la boîte et le robot dans les bonnes cases.
Ce qui suit est une autre manière typique de déterminer des sous-tâches. Il est raisonnable de supposer que tout l’espace intérieur dans une position est nécessaire pour la solution. Ceci veut dire que si la position initiale a plein de gros espaces vides, comme la zone 2×3 vide dans l’exemple ci-dessus, on doit déterminer à quoi sert cet espace. Peut-être est-il est nécessaire pour permettre au robot de contourner une boîte ou pour poser une boîte le temps de libérer de la place ailleurs. Dans ce deuxième cas on se demande ensuite quelle boîte? Et comment mettre la boîte dans cet espace?
3) Formuler des Restrictions sur le Chemin de Solution
Dès la position initiale, sans essayer de coups, on peut identifier plein de restrictions sur la solution. Voici quelques exemples :
3.1) Il existe un couloir qu’une boîte ne peut pas traverser mais dans lequel elle peut pourtant entrer, alors l’espace au bout du couloir sera bloqué.
Une boîte dans la case A ne pourra jamais atteindre B en passant par le coin, ni l’inverse.
3.2) On ne peut atteindre un certain point rouge que par un côté même s’il y a de l’espace sur d’autres côtés.
Par exemple) Le point ne peut pas être atteint par une boîte de dessous.
3.3) On ne peut pas déplacer une certain boîte dans une certaine direction et donc on ne peut la placer que sur un seul point rouge.
Ex) Cette boîte ne peut atteindre que le point rouge sur sa gauche.
3.4) Puisque certains point rouges ne sont accessibles que par certains côtés, l’ordre dans lequel les points seront occupés est déjà déterminé.
Ex. Dans la position suivante le point rouge à gauche doit être occupé avant celui à droite.
3.5) Il est évident dès le départ quel point il faudra couvrir en dernier car l’espace doit d’abord servir à déplacer d’autres boîtes.
Ex) Pour pouvoir pousser une boîte à gauche il faudra utiliser la case occupée par le point le plus à droite, donc il sera le dernier point recouvert par une boîte.4) D’autres Heuristiques
4.1) Il faut essayer toute séquence de poussées réversible, même si le robot doit effectuer beaucoup de déplacements pour défaire ces poussées. Cet exercice a l’air inutile mais la nouvelle position résultante peut révéler la façon de procéder.
4.2) S’il y a une ligne droite séparant tous les points d’au moins une boîte, alors cette boîte doit traverser cette ligne. Si ceci est impossible alors la position est morte. S’il n’existe qu’une seule façon pour faire traverser la boîte alors on identifie ainsi une forte restriction sur le chemin de solution.
Exemple d’une Solution Complète (Jeu 8)
(1)
On assigne des coordonnées pour pouvoir décrire les cases. Par exemple, le robot commence dans la case G1.
Au début le robot n’a que 2 options : a) entrer dans le trou G3, ou b) entrer dans le trou E3. Entrer dans le trou G3 ne lui permettra que de pousser la boîte dans B3 dans B1 → position morte. Alors le robot entrer dans le trou E3 et se met sur B2 :
(2)
Les seules poussées possibles sont a) la boîte B3 à B4 (pas B5, ce sera la mort) ou la boîte C2 à la droite.
On se rend compte qu’on ne pourra pas pousser les boîtes sur un chemin qui passe par G3 car il sera impossible de les pousser à gauche après. (voir 1.2)
Cependant, pour les déplacer à travers le trou B3,C3 il faut y faire de la place, donc il va falloir mettre une ou deux boîtes sur la droite pour revenir les chercher après.
On se rend compte que la boîte B3 ne peut se déplacer que sur la ligne B alors elle finira certainement sur le point B4.
Pour pouvoir mettre des boîtes sur C4 et les pousser à droite, le robot doit pouvoir se mettre sur A4, mais pour y accéder de dessous, il faut poser la boîte B3 sur B2 et les cases B3, C3, C2 doivent être vides, alors il faut dégager deux boîtes et les mettre en bas à droite.
Alors, pour libérer la place occupée par la boîte C2 et mettre le robot en haut à gauche, on pourra suivre l’exemple 2.1 et atteindre
(3)
Mais on ne peut pas pousser les boîtes A3 et B3 en bas. La seule option restante dans la position (2) est de pousser d’abord la boîte de B3 à B4 et ensuite d’effectuer les coups pour atteindre la position (3). On obtient
(4)
Maintenant on peut avancer en poussant la boîte C3 à C2 et puis en déplaçant le robot pour pousser la boîte F2 à G2 et ensuite à G3 :
(5)
Comme mentionné ci-dessus, il faut libérer les cases B3, C3, C2 pour pousser la boîte B4 à B2 donc il faut poser la boîte C2 temporairement sur G2. On obtient :
(6)
Ensuite on peut poursuivre notre programme est pousser la boîte G2 à C4 pour ensuite la pousser à droite :
(7)
Attendez : on doit pousser la boîte C4 à droite, mais de combien de cases? Il faut toujours pousser la boîte G3 le long du même chemin nécessaire pour que le robot atteigne G4. Pour ce faire il faut pousser la boîte C4 à F4, déplacer le robot à G4, et pousser la boîte G4 à G3 :
(8)
Pour pousser la boîte G2 à gauche le robot doit refaire tout le chemin dans le sens antihoraire jusqu’à H2.
(9)
Il ne reste que des coups simples : pousser la boîte G2 à C2, C4, D4.
(10)
Ensuite on pousse la boîte B2 à B4 et le robot se met sur G4 pour pousser la boîte F4 sur le point E4.
TERMINÉ.
Par exemple, on dit que quelqu’un est insolvable s’il doit de l’argent mais n’a pas d’argent liquide et il n’a pas de reçu attestant un emprunt de l’argent à un tiers, ou il a un reçu attestant un emprunt de l’argent à un tiers mais cette tierce personne est insolvable elle aussi.
Cette explication du mot insolvable utilise le mot insolvable alors elle est récursive.
Exemple:
Les personnes A,B,C n’ont pas d’argent, et chacune d’entre elles doit de l’argent à D.
A a un reçu pour avoir fait un emprunt à B,
B a un reçu pour avoir fait un emprunt à C,
C a un reçu pour avoir fait un emprunt à A
Mais l’ensemble est insolvable, chacune d’entre elles.
Une situation similaire mais différente :
Les personnes A,B,C n’ont pas d’argent, et chacune d’entre elles doit de l’argent à D.
A a un reçu pour avoir fait un emprunt à B,,
B a un reçu pour avoir fait un emprunt à C,
C a un reçu pour avoir fait un emprunt à F
Si la personne F a de l’argent, alors ni A ni B ni C ne seront insolvables.
Pour faire la différence entre ces deux cas il faut bien regarder toutes les relations et non une seule, car la susdite définition d’insolvable est récursive.
关于推箱子游戏的建议
符号
本指南将使用以下术语：
- 步数： 工人的步数，推或不推箱子都计入。
- 路径： 一系列动作。
- 位置： 工人和所有箱子在某地特定地方的情况。
- 解决方案： 所有箱子都在红点上的位置。
- 解决方案路径： 从初始位置到解决方案的一系列动作。
- 死局： 无法达到解决方案的路径。
总体战略
最短的解决方案可能包含100,300甚至1000个步数。 （我们最简单的游戏1需要73个动作，游戏8需要126个动作）。 如果平均每个移动有两种可能性，并且解决方案需要100次移动，那么盲目搜索将需要搜索2100个路径以找到解决方案。 即使对于计算机，这也是不可能的。 因此，我们需要：
- 尽早明确一个位置是不是死局，
- 将总体目标分解为子任务。 如果100个步骤的解决方案路径可以分解为，例如，10个子任务，那么问题的复杂性将大大降低。 此外，有可能推断出完成子任务的顺序，然后整个问题变得容易解决，
- 找到解决方案路径上的限制，
- 想想其他探索方法。
关于1：今早找出死局
1.1：有时判断一个位置是否是死局很容易，只需要查看一个单独的箱子附近的情况。 要做的只是“本地”检查。 如果一个箱子不在一个点上并且不能水平移动，也不能垂直移动，那么该位置就是死局。 箱子可能被墙壁或其他也不能移动的箱子挡住。
例如：
1.2：如果箱子靠近墙壁并且它可以被推动但是只能沿着同一侧的墙壁被推动而且它可以到达的任何地方都不是一个点，那么这个位置也是死局，虽然稍微难看出来一点。
例如：
在这种概括的情况中，箱子靠近墙壁并且可以移动到其侧面没有墙壁的地方（下面的位置A），但是将箱子推到A附近后，小工人无法到达A。
例如：
这三种情况可以只看箱子就决定，而不需要移动工人。 因此，可以在初始位置检查是否有此类情况，并可以标记出这些禁止的地方，比如说用！标记。 这样箱子就永远不会被推到这里。
1.4：在进一步概括的情况中，小工人想要到达地点A就不得不把另一个箱子推到一个禁止的地方。
例如：
这种解释是循环的[1], 也就是说，它用死局来描述死局。 这种死局更难以识别，因为它们无法通过“本地”检查发现，并且可能需要一些走步骤来测试。
关于2：制定子任务
子任务的例子如下：
- 把小工人从A移到B，
- 把某个箱子从A移到B
完成这些任务都不应该制造出死局。
（a）的例子：工人怎么样才能绕过箱子到达A？
→→→→
必须要有空间工人才能在箱子周围走动。 如果空的空间较少，那么工人无法在不产生死局的情况下绕过箱子。
如果玩家把大量子任务的路线烂熟于心，那么就可以节省很多时间，在本例中是一个9个步骤。更重要的是，玩家这道这个子任务是可能的，所以不会放弃。
与子任务相关的一个问题是如何找到它们。 例如，当反向解决问题时，就会出现子任务。 假设只能从一侧由一个箱子到达某个点，那么就需要将该箱子推向特定方向。 为了做到这一点，工人需要到达它的另一边。任务就可能是将箱子和工人放在正确的位置。
提出子任务的另一个典型示例如下。 安全地假设解决方案需要一个位置的所有内部空间。 这意味着，如果初始 位置具有庞大的内部空间，如上例中的2*3的空区域，这些空间用来干什么。可能是工人需要这个空间来绕过一个箱子，或者用于临时放一个箱子以便在其他地方释放空间。 因此，如果多余的空间能够临时存放一个箱子，那哪个箱子需要临时存放呢？怎么把这个箱子推到这个中间停放点？
关于3：制定解决方案路径的限制
只需通过查看位置而不尝试移动就可以对解决方案路径进行许多限制。 例如：
3.1：有一个箱子可以进入但不可能贯穿的走廊，因此走廊末端的空间永远不能从走廊结束的一侧到达。
例如，B上的一个盒子永远无法到达A点，并且A上的盒子无法通过拐角到达B。
3.2：即使在不同侧面有空间，某个点也只能从一侧到达。
例如，箱子无法从下面到达的点
3.3：某个盒子永远不能在某个方向上移动，因此只能到达一个特定的点。
例如，该箱子只能到达其左侧的点。
3.4：因为某些点只能从特定的方向到达，所以它决定了到达不同的点的顺序。
例如，在以下位置，左边的点必须在它右边的点之前到达。
3.5：最后到达哪一点可能很清楚，因为工人需要空间来向某个方向推动一个盒子。
例如，工人需要站在最右边的点的空间，并将一个盒子推到左边，所以最右边的点是最后一个到达的点（与上图相同）。关于4：其他探索
4.1：可以并且应该尝试任何可以反转的推动顺序，即使这意味着工人必须走很长的路才能从另一侧推箱子以反转这些推动。即使这样的练习看起来毫无意义，但新位置也可能为如何开展提供新的可能性。
4.2：如果有一条直线将所有点与至少一个箱子分开，则该箱子必须越过该线。如果这是不可能的，那么该位置就是死局。如果盒子只有一种方式穿过该线，则这就是对解决方案路径的巨大限制。
完整解决方案示例，游戏8
(1)
中文：为了标记点，我们引入了坐标。 例如，工人最初在G1点。/p>
最初，工人只有两个选项：A，穿过洞G3，或B，穿过洞E3。穿过G3只能让工人将B3的盒子推到B1，导致死局。所以工人穿过E3到达B2
(2)
我们可以做的唯一移动是A，将箱子从B3推到B4（不是B5，B5是死局），或者是从C2推到右边。
我们意识到盒子不能移动到通过G3的路线上的点，因为在这个它们之后就不能移动到左边了，如1.2中所示。
但是为了让它们通过洞B3，C3，我们需要在这个区域内有空间，所以我们需要在右边停放一个或两个箱子，之后又必须把它们移回来。
我们还意识到盒子B3只能在B线上移动，因此最终必须在B4点结束。
要在C4上移动后面的箱子然后将它们推到右边，工人必须能够移动到A4但是从下面到B4，箱子B3必须在B2处且空间B3，C3，C2必须是空的，所以两个盒子必须移开并停在右下方。
所以，为了让箱子C2不挡路并让工人到达左上方，我们可以使用示例2.1
(3)
但是把箱子A3或B3推下去并不起作用。 我们在位置2唯一的另一个选择是首先将箱子B3推到B4，然后进行到位置3的移动。我们得到了
(4)
现在我们可以通过将箱子C3向下推到C2并与工人一起移动以将方框F2推到G2和G3：
(5)
如上所述，我们需要空间B3，C3，C2空出来，并将箱子B4下移到B2，所以我们需要暂时将箱子C2放在G2。我们得到：
(6)
简体中文：现在我们可以按照我们之前的计划将箱子G2推到C4，以便将其推向右边：
(7)
问题是我们要将盒子C4推到多右边。因为我们仍然需要通过相同的路径推箱子G3，所以我们需要让工人到G4并且为此我们要将箱子C4推到F4并将工人移动到G4以将G4推到G3：
(8)
中文：要将框G2向左移动，工人需要逆时针方向向后移动到H2。
(9)
剩下的很简单：将框G2推到C2，C4，D4
(10)
然后将框B2推到B4，工人移动到G4，最后把箱子F4推到E4。
完成。
如果某人欠其他人的钱并且没有现金，也没有收到借入别人钱的收据，或者有借款收据但借钱给他的人已破产，则这个人就是破产了。
破产这个词的解释使用了破产这个词，因此它被称为循环。
例如：
A，B，C三人没有钱，且都欠D的钱，
A有一张向B借款的收据，
B有一张向C借款的收据，
C有一张向A借钱的收据
但他们是一群破产者，每个人都是。
类似但不同的情况：
A，B，C三人没有钱，且都欠D的钱，
A有一张向B借款的收据，
B有一张向C借款的收据，
C有一张向F借钱的收据
因为F可能有钱，那么A,B,C可能都不会破产。
区分这两种情况，需要关注所有关系，而不仅仅是单独的一个关系，因为上述破产定义是循环的。
توصیه هایی در راستای چگونگی بازی سوکوبان
نوشتار
عبارات زیر در حین این راهنمایی استفاده می شوند:
- حرکت: یک قدم کارگر چه جعبه ای را حرکت بدهد چه ندهد.
- مسیر: دنباله ای از حرکات.
- موقعیت: کل این مساله با در نظر گرقتن کارگر و همه ی جعبه ها در یک موقعیت خاص.
- پاسخ: موقعیتی که در آن هر جعبه ای روی یک نقطه قرار دارد.
- مسیر پاسخ: دنباله ای از حرکات از موقعیت اصلی به پاسخ.
- موقعیت مرده: موقعیتی که از آن پاسخ نمی تواند به دست آید.
استراتژی کلی
کوتاهترین پاسخ ممکن است شامل ۱۰۰، ۳۰۰ یا حتی ۱۰۰۰ حرکت. ساده ترین بازی ۱ ما ۷۳ حرکت لازم دارد، بازی ۸، ۱۲۶ حرکت لازم دارد. اگر به طور متوسط، فرض کنید، ۲ احتمال برای هر حرکت و پاسخ ۱۰۰ حرکت می خواهد، آنگاه یک جستجوی جامع ممکن است نیازمند جستجوی ۲۱۰۰ مسیر برای پیدا کردن پاسخ باشد. حتی برای رایانه ها این ممکن نیست. در نتیجه ما لازم است که:
- زود تشخیص دهیم اگر موقعیتی مرده است،
- هدف نهایی را به چند کار زیرمجموعه ای تقسیم کنید. اگر یک مسیر پاسخ ۱۰۰ حرکتی بتواند به مثلا، ۱۰ زیر شاخه تقسیم شود، آنگاه پیچیدگی مساله به شدت کاهش پیدا می کند. . به علاوه، ممکن است که بتوان ترتیبی که در آن زیرشاخه باید انحام شود را کاهش داد و آنگاه کل مساله برای حل شدن ساده می شود،
- اولین محدودیت برای مسیر پاسخ،
- به ابتکارهای دیگر فکر کنید.
درباره ی ۱: تشخیص زودهنگام موقعیت های مرده
۱. ۱: گاهی آسان است که تصمیم بگیریم آیا موقعیتی مرده است، فقط کافی است به همسایگی یک جعبه ی تنها نگاه کرد. تنها چیزی که لازم است یک بازرسی موضعی است. اگر جعبه ای روی یک نقطه قرار نگرفته است و نمی تواند به صورت افقی و عمودی حرکت کند، آنگاه آن موقعیت مرده است. جعبه ممکن است با دیوار و یا جعبه های دیگر بلوکه شده باشد که باز هم نمی تواند حرکت کند.
مثال ها:
۱.۲: این اندکی سخت تر است که ببینیم که موقعیتی مرده است اگر که جعبه در کنار دیوار قرار دارد و می تواند هل داده شود اما فقط در راستای دیوار و در جهت یکسان، و هیچ یک از موقعیت هایی که این جعبه می تواند به آن برسد نقطه نمی باشد.
مثال ها:
۱.۳: در این تعمیم جعبه در کنار دیوار قرار دارد و می تواند به موقعیتی که دیوار در کنارش قرار نداشته باشد، حرکت داده شود, نقشه ی A در زیر، اما آن موقعیت همسایه ی خالی الف نمی تواند توسط کارگر بعد از هل دادن جعبه به کنار A به دست آید.
مثال ها:
این سه مورد می توانند به صورت موضعی و بدون حرکت کردن کارگر تصمیم گیری شوند. بنابراین می توانند در موقعیت ابتدایی بررسی شوند و می توان مکان ها را به عنوان ممنوع مشخص کرد، مثلا با ! ، به گونه ای که یک جعبه هرگز نمی تواند به آن مکان ها هل داده شود.
۱.۴: در تعمیم بعدی، مکان A می تواند توسط کارگر به دست آید اما به قیمت اینکه قرار دادن یک جعبه ی دیگر در یک مکان ممنوع.
مثال ها:
این توضیحات بازگشتی می باشد [1], یعنی، یک مکان مرده را با استفاده از کلمه های موقعیت مرده مشخص می کند. چنین موقعیت های مرده ای سخت تر قابل تشخیص هستند زیرا که نمی توانند با بازرسی موضعی پیدا شوند و ممکن است تست حرکت ها لازم باشد.
در مورد ۲: فرمول بندی کردن کارهای زیرمجموعه ای
مثال هایی از کارهای زیرمجموعه ای:
- کارگر را از A به B حرکت دهید،
- یک جعبه ی مشخص را از A به B حرکت دهید
که هر یک از این کارها قرار است که بدون به وجود آوردن موقعیت مرده به دست آید.
مثالی از: اینکه چگونه کارگر می تواند از یک جعبه برای رسیدن به A
بگذرد:→→→→
از آنجایی که کارگر باید اطراف جعبه قدم بردارد، همه ی فضای خالی لازم می باشد. اگر فضای خالی کمتری وجود داشته باشد، آنگاه کارگر نمی تواند از جعبه بدون تولید موقعیت مرده بگذرد.
اگر کسی تعداد زیادی ازاین کارهای زیرمجموعه ای را عمیقا با شکل های آنها می داند، آنگاه می تواند زمان زیادی را با صرف نکردن برای فکر کردن درباره ی آن ذخیره کند، در اینجا این مسیر ۹ حرکتی. با اهمیت تر از آن، فکر مردن به اینکه یک کاز غیر ممکن است باعث تسلیم شدن نخواهد شد.
یک سوال مرتبط با کار زیرمجموعه ای این است که چگونه آنها را پیدا کنیم. به عنوان مثال، کارهای زیرمجموعه ای در زمان حل کردن مساله به صورت برعکس پدیدار می شوند. فرض کنید یک نقطه ی مشخص فقط می تواند از یک طرف فقط یک جعبه در دسترسی قرار بگیرد. در نتیجه این جعبه لازم است که در یک جهت خاص حرکت داده شود. برای انجام این کار، ازم است که کارگر به طرف دیگر آن برسد. یک کار می تواند آوردن جعبه و کارگر به موقعیت درست باشد.
یک مثال متداول دیگر از پیدا کردن کارهای زیر مجموعه ای مثال این است: می توان با خیال راحت فرض کرد که همه ی فضای داخل یک موقعیت برای پاسخ لازم است. این به ین معنی است که اگر موقعیت ابتدایی فضای داخلی حجیمی دارد، مثلا ۲ ضربدر ۳ مساحت خالی در مثال بالا، آنگاه می توان پرسید که هدف این فضا چیست. می تواند این باشد که این فضا لازم است برای کارگر که از جعبه ها عبور کند و یا اینکه استفاده می شود برای پارک موقت یک جعبه به فضای خالی در جای دیگر به صورت فوری. بنابراین اگر فضای وسیع قابلیت این را دارد که جعبه را به صورت موقت نگه داری کند آنگاه آن جعبه کدام می تواند باشد؟ چگونه می توان این جعبه را به نقطه پارکیگ میانی رساند؟
درباره ی ۳: فرمولسازی کردن محدودیت ها روی مسیر پاسخ
محدودیت های زیادی روی مسیر پاسخ قرار دارند که با نگاه کردن به موقعیت و بدون امتحان کردن هیچ حرکتی ممکن هستند. به عنوان مثال:
۳.۱: یک راهرو وجود دارد که می توان با یک جعبه وارد آن شد، اما جعبه هیچوقت نمی تواند در طول کل راهرو حرکت کند و در نتیجه فضای انتهایی راهرو هرگز از طرفی که آن به پایان می رسد مورد دسترسی قرار نمی گیرد.
مثال: با رفتن به گوشه، نقطه ی A هرگز نمی تواند با جعبه ای که در B قرار دارد به دست آید و B نمی تواند با جعبه ای که در A قرار دارد به دست آید.
۳.۲: یک نقطه ی خاص فقط می تواند از یک طرف مورد دسترسی قرار گیرد حتی اگر فضای خالی در طرف های دیگر وجود داشته باشد.
مثال: یک نقطه نمی تواند توسط جعبه ای از پایین مورد دسترسی قرار گیرد.
۳.۳: یک جعبه ی خاص هرگز نمی تواند در یک جهت خاص خرکت داده شود و در نتیجه فقط می تواند به یک نقطه ی خاص دست یابد.
مثال: جعبه فقط می تواند به نقطه ی سمت چپش دست یابد.
۳.۴: از آنجایی که نقطه ها می توانند توسط جعبه ها فقط از بعضی طرف ها مورد دسترسی قرار گیرند، این ترتیبی که در آن نقطه ها باید اشغال شوند را تعیین می کند.
مثال: در موقعیت زیر نقطه ی سمت چپ باید نقطه ی سمت راستش اشغال شود.
۳.۵: این ممکن است که واضح باشد که کدام نقطه لازم است در آخر پوشانده شود، زیرا که فضا برای کارگر لازم است که بتواند جعبه را در یک مسیر خاص هل دهد.
مثال: فضای راست ترین نقطه برای کارگر لازم است تا بایستد و و جعبه را به چپ هل دهد ، بنابراین راست ترین نقطه، آخرین نقطه ایست که باید اشغال شود.درباره ی ۴: ابتکارهای دیگر
۴.۱: هر دنباله ای از هل دادن ها که بتواند معکوس شودمی تواند و باید امتحان شود، حتی اگر به این معنی باشد که کارگر مجبور است راه طولانی برود تا بتواند از طرف دیگر این هل دادن ها را معکوس کند. حتی اگر همچین تمرینی بی ثمر به نظر آید، موقعیت جدید ممکن است که احتمالات جدیدی را برای چگونگی ادامه دادن باز کند.
۴.۲: اگر یک خط مستقیمی وجود دارد که همه ی نقطه ها را از حداقل یک جعبه جدا کند، آنگاه این جعبه باید از آن خط بگذرد. اگر این ممکن نیست آنگاه موقعیت مرده است. اگر برای جعبه فقط یک راه وجود دارد که از آن خط بگذرد آنگاه این یک محدودیت قوی برای مسیر پاسخ است.
مثالی از پاسخ کامل: بازی ۸
(1)
ما مختصات را برای نشانه گذاری نقطه ها معرفی می کنیم. برای مثال، کارگر در آغاز در نقطه ی G1 می باشد.
در آغاز کارگر فقط دو گزینه دارد: الف: الف: رفتن به حفره ی G3 ، یا ب: رفتن به حفره ی E3. رفتن به G3 فقط به کارگر اجازه می دهد که جعبه را در B3 به B1 هل دهد، نتیجه مرگ است. بنابراین کارگر از حفره ی E3 به B2 می رود:
(2)
تنها هل دادن هایی که می توانیم اعمال کنیم الف: جعبه ی B3 تا جعبه ی B4 است یا جعبه ی C2 به راست است.
ما تشخیص می دهیم که جعبه ها نمی توانند به نقاط در مسیر G3 حرکت داده شوند زیرا که آنها بعد از همه ی اینها هرگز نمی توانند به چپ حرکت داده شوند (۱.۲ را ببینید).
اما در راستای حرکت دادن آنها از حفره ی B3,C3 ما فضای این ناحیه را احتیاج داریم، بنابراین لازم است یک یا دو جعبه را به راست حرکت دهیم و مجبوریم بعد از همه ی اینها، آنها را برگردانیم.
ما همچنین تشخیص می دهیم که جعبه ی B3 فقط می تواند روی خط B B حرکت داده شود و در نتیجه در نهایت مجبور است که در نقطه ی B4 خاتمه یابد.
برای حرکت جعبه های بعدی روی C4 و آنگاه هل دادن آنها به سمت راست، کارگر باید قادر باشد که به A4 حرکت کند اما برای رسیدن به آنجا از پایین، جعبه ی B3 باید در B2 باشد و فضاهای B3, C3, C2 باید خالی باشند، بنابراین دو جعبه باید از مسیر خارج شوند و در پایینتر سمت راست پارک شوند.
بنابراین، برای خارج کردن جعبه ی C2 از مسیر و رساندن کارگر به بالا سمت چپ، می توانیم از مثال ۲.۱ استفاده کنیم و برسیم
(3)
اما پایین هل دادن جعبه های A3 یا B3 نتبجه نخواهد داشت. تنها گزینه ی دیگر که در موقعیت ۲ که داشتیم این است که در ابتدا جعبه ی B3 را تا B4 هل دهیم و آنگاه حرکت هایی را اعمال کنیم که منجر به موقعیت ۳ می شوند. بدست می آوریم
(4)
اکنون می توانیم با هل دادن جعبه ی C3 به پایین تا C2 و حرکت کردن با کارگر به اطراف برای هل دادن جعبه ی F2 به G2 و G3 :
(5)
همانطور که در بالا مطرح شد، ما فضاهای B3,C3,C2 را خالی احتیاج داریم و لازم است جعبه ی B4 را پایین تا B2 برسانیم، بنابراین لازم است که جعبه ی C2 به طور موقت روی G2 . پارک کنیم. بدست می آوریم:
(6)
اکنون می توانیم نقشه ی اولیه مان را دنبال کنیم و جعبه ی G2 . را در راستای هل دادنش بعدا به سمت راست به C4 . هل دهیم:
(7)
سوال این است که چه مقدار به سمت راست باید آن جعبه ی C4 . را هل دهیم. زیراکه هنوز لازم است که جعبه ی G3 را در طول مسیری که لازم است کارگر را به G4 G4 برسانیم، هل دهیم و همچنین جعبه ی C4 را تا F4 هل دهیم و کارگر را به G4 برسانیم با G4 را به G3 هل دهد:
(8)
برای هل دادن جعبه ی G2 به چپ، لازم است کارگر تمام راه را در خلاف حرکت عقربه ی ساعت تا H2 برگردد.
(9)
از این پس آسان است: جعبه ی G2 به C2, C4, D4 هل داده می شود
(10)
سپس جعبه ی B2 به B4 هل داده می شود و کارگر به G4 حرکت می کند با سرانجام جعبه ی F4 را روی نقطه ی E4 هل دهد.
تمام شد.
یک نفر ورشکست است اگر آن نفر به شخص دیگری پول بدهکار است و پولی ندارد و یا رسیدی از اینکه پولی از شخص دیگری قرض گرفته ندارد، و یا رسید از اینکه از شخص دیگری پول قرض گرفته دارد اما آن شخص ورشکست شده است.
این توضیح از کلمه ی ورشکست خود کلمه ی ورشکسترا استفاده می کند، و در نتیجه بازگشتی نامیده می شود.
مثال:
افراد A,B,C هیچ پولی ندارند، همه ی آنها مقداری پول به شخص D بدهکارند،
A رسید دارد که از B پول قرض گرفته،
B رسید دارد که از C پول قرض گرفته،
C رسید دارد که از A پول قرض گرفته،
اما اینها به عنوان یک گروه ورشکست هستند، هر یک از آنها.
پاسخی مشابه اما متفاوت:
افراد A,B,C هیچ پولی ندارند، همه ی آنها مقداری پول به شخص D بدهکارند،
A رسید دارد که از B پول قرض گرفته،
B رسید دارد که از C پول قرض گرفته،
C رسید دارد که از F پول قرض گرفته،
از آنجایی که ممکن است شخص F پول داشته باشد، ممکن است که هیچ یک از A,B,C ورشکست نباشند.
برای تشخیص دادن این دو مورد لازم است که به همه ی روابط نگاه کرد، نه فقط به یک مورد، چرا که تعریف بالا از ورشکست بازگشتی است.
Follow or subscribe for updates: