Sokoban

300000

Sokoban^©

Tổng số người chơi: 1129075
Tổng số trận thắng: 153167

Gợi ý về cách chơi Sokoban

Chú thích

Các thuật ngữ sau sẽ được sử dụng xuyên suốt bản hướng dẫn này:

Di chuyển: một bước của người thợ dù đẩy hay không đẩy một ô.
Lộ trình: một chuỗi các bước di chuyển.
Vị trí: toàn bộ vấn đề liên quan tới người thợ và tất cả các hộp ở một nơi nhất định.
Giải pháp: một vị trí mà mỗi ô đều nằm trên một dấu chấm.
Lộ trình giải pháp: chuỗi chuyển động từ vị trí ban đầu đến giải pháp.
Vị trí chết: một vị trí mà từ đó không thể đạt được giải pháp.

Chiến lược chung

Lời giải ngắn nhất có thể chứa 100, 300 hoặc thậm chí 1000 nước đi. (Ván 1 đơn giản nhất của chúng ta đã cần 73 nước đi, ván 8 cần 126 nước đi). Nếu trung bình có 2 khả năng xảy ra cho mỗi lần di chuyển và giải pháp thì cần đến 100 lần di chuyển thì một sự tìm kiếm thủ công đầy khó khăn sẽ yêu cầu nghiên cứu 2^100 lộ trình để tìm ra giải pháp. Ngay cả đối với máy tính, điều này là không thể. Do đó, chúng ta cần phải:

Nhận biết sớm một vị trí đã chết,
Chia mục tiêu tổng thể thành các nhiệm vụ nhỏ. Nếu một lộ trình giải pháp gồm 100 bước đi có thể được chia nhỏ thành 10 nhiệm vụ nhỏ thì mức độ phức tạp của vấn đề sẽ giảm đáng kể. Hơn nữa, có thể suy ra thứ tự mà các nhiệm vụ nhỏ cần phải hoàn thành và sau đó toàn bộ vấn đề trở nên dễ giải quyết hơn,
Tìm hạn chế trên lộ trình giải pháp,
Hãy suy nghĩ về các phương pháp khác.

Phần 1: Nhận biết sớm các vị trí chết

1.1) Đôi khi rất dễ dàng để quyết định xem một vị trí đã chết hay chưa, ta chỉ cần nhìn vào vùng lân cận của một ô duy nhất. Tất cả những gì cần làm là một cuộc kiểm tra 'cục bộ'. Nếu một hộp không đứng trên một dấu chấm và không thể di chuyển theo chiều ngang và cả chiều dọc, thì vị trí đó đã chết. Hộp có thể bị chặn bởi tường hoặc bởi các hộp khác và cũng không thể di chuyển được.

Ví dụ:

1.2) Sẽ hơi khó nhận ra rằng một vị trí đã chết nếu chiếc hộp nằm cạnh một bức tường và nó có thể được đẩy nhưng chỉ dọc theo bức tường cùng phía và nó không thể tới được bất kỳ chỗ dấu chấm nào.

Ví dụ:

1.3) Tổng hợp lại, hộp nằm cạnh một bức tường và có thể được di chuyển đến một nơi không có bức tường ở phía bên của nó (vị trí A bên dưới), nhưng người thợ không thể tới được địa điểm lân cận đang trống đó sau khi đẩy hộp bên cạnh A.

Ví dụ:

Ba trường hợp này có thể được quyết định cục bộ và không cần di chuyển người thợ. Vì vậy, chúng có thể được kiểm tra ở vị trí ban đầu và người ta có thể đánh dấu những nơi bị cấm, chẳng hạn dùng ! để một hộp có thể không bao giờ bị đẩy lên một nơi như vậy.

1.4) Nói một cách tổng quát hơn, người thợ có thể đến được nơi A nhưng chỉ khi đánh đổi đặt một chiếc hộp khác vào một nơi bị cấm.

Ví dụ:

Lời giải thích này là đệ quy^[1], tức là nó đặc trưng cho một vị trí chết bằng cách sử dụng các từ vị trí chết. Những vị trí chết như vậy khó nhận ra hơn vì chúng không thể được phát hiện bằng cách kiểm tra tại chỗ và có thể cần đến các lượt di chuyển thử.

Phần 2: Lập Các Nhiệm Vụ Nhỏ

Ví dụ về các nhiệm vụ phụ là:

Di chuyển người thợ từ A đến B,
Di chuyển một ô nhất định từ A sang B

Mỗi một nơi trong số những nhiệm vụ này phải được hoàn thành mà không tạo ra một vị trí chết.

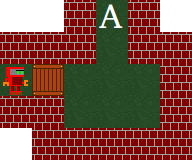
Ví dụ cho (a): Làm thế nào để người thợ có thể vượt qua một chiếc hộp để đến A:

→

Tất cả không gian trống là cần thiết vì người thợ phải đi vòng quanh chiếc hộp. Nếu có ít không gian trống hơn thì người thợ không thể vượt qua hộp mà không tạo ra vị trí chết.

Nếu một người biết nhiều nhiệm vụ nhỏ như vậy với hình dạng của hành lang thuộc lòng thì người ta sẽ tiết kiệm được nhiều thời gian mà không cần phải suy nghĩ về nó, đây là lộ trình 9 bước đi. Quan trọng hơn là một người sẽ không bỏ cuộc bởi vì một người nghĩ rằng nhiệm vụ nhỏ này là không thể.

Một câu hỏi liên quan đến nhiệm vụ nhỏ là làm thế nào để tìm chúng. Ví dụ: các nhiệm vụ nhỏ xuất hiện khi giải quyết vấn đề ngược lại. Giả sử một dấu chấm nhất định chỉ có thể đạt được từ một phía và chỉ bằng một hộp. Do đó, hộp này cần được đẩy theo một hướng cụ thể. Để làm như vậy, người lao động cần phải đi đến phía bên kia của nó. Một nhiệm vụ có thể là đưa hộp và người thợ vào đúng vị trí.

Một ví dụ điển hình khác về việc đưa ra một nhiệm vụ nhỏ là như sau. Có một điều chắc chắn khi giả định rằng tất cả không gian nội thất ở một vị trí là cần thiết cho giải pháp. Điều đó có nghĩa là, nếu vị trí ban đầu có không gian bên trong rộng rãi, giống như diện tích trống 2 x 3 trong ví dụ trên, thì người ta có thể tự hỏi mục đích của không gian đó là gì. Có thể là do người thợ cần đến để vượt qua một chiếc hộp hoặc nó được sử dụng để đặt tạm một chiếc hộp nhằm giải phóng không gian ở một nơi khác ngay lập tức. Vậy nếu không gian rộng có khả năng cất giữ một chiếc hộp tạm thời thì đó có thể là chiếc hộp nào? Làm thế nào người ta có thể đưa chiếc hộp này đến điểm đặt trung gian này?

Phần 3: Trình bày Hạn Chế trên Lộ Trình Giải Pháp

Có rất nhiều hạn chế đối với lộ trình giải pháp có thể chỉ bằng cách nhìn vào vị trí mà không thử di chuyển. Ví dụ như:

3.1) Có một hành lang có thể tiến vào bằng một chiếc hộp nhưng chiếc hộp không bao giờ có thể di chuyển qua toàn bộ hành lang và do đó không gian ở cuối hành lang không bao giờ có thể đến được từ phía nơi hành lang kết thúc.

ví dụ, Điểm A không bao giờ có thể chạm tới được bằng một chiếc hộp nằm trên B và không thể chạm tới điểm B bằng một chiếc hộp nằm trên A bằng cách đi qua góc.

3.2) Một dấu chấm nhất định chỉ có thể đạt được từ một phía mặc dù có không gian trống ở các phía khác nhau.

eg) The dot can not be reached by a box from below.

3.3) Một hộp nhất định không bao giờ có thể di chuyển theo một hướng nhất định và do đó chỉ có thể đạt đến một dấu chấm cụ thể.

ví dụ, Cái hộp chỉ có thể chạm tới dấu chấm ở bên trái của nó.

3.4) Bởi vì các dấu chấm có thể được tiếp cận bởi các hộp chỉ từ một số phía nên nó xác định thứ tự các dấu chấm phải được chiếm.

ví dụ, Ở vị trí sau dấu chấm bên trái phải được chiếm trước dấu chấm bên phải của nó.

3.5) Có thể thấy rõ rằng điểm nào cần được che lại cuối cùng bởi vì không gian là cần thiết để người thợ đẩy một hộp theo một hướng nhất định.

ví dụ: Cần có khoảng trống của dấu chấm ngoài cùng bên phải để công nhân đứng và đẩy một ô sang trái, vì vậy dấu chấm ngoài cùng bên phải là ô cuối cùng được chiếm, (trong cùng hình trên).

Phần 4: Các Phương Pháp Khác

4.1) Bất kỳ chuỗi đẩy hộp nào có thể đảo ngược đều có thể và nên được thử, ngay cả khi điều đó có nghĩa là người thợ phải đi một quãng đường dài để đẩy từ phía khác để đảo ngược những cú đẩy này. Ngay cả khi một bài tập như vậy trông có vẻ vô nghĩa, vị trí mới có thể mở ra những khả năng mới về cách tiến hành.

4.2) Nếu có một đường thẳng ngăn cách tất cả các dấu chấm khỏi ít nhất một ô, thì ô này phải cắt qua đường thẳng đó. Nếu điều này là không thể thì vị trí đã chết. Nếu chỉ tồn tại một đường để hộp đi qua đường đó thì đây là một hạn chế lớn đối với lộ trình giải pháp.

Ví dụ về Giải pháp Hoàn chỉnh, Trò chơi 8

(1)

Chúng tôi giới thiệu tọa độ để đánh dấu các điểm. Ví dụ, ban đầu người thợ đang ở điểm G1.

Ban đầu người thợ chỉ có 2 lựa chọn: A, đi qua lỗ G3, hoặc B, đi qua lỗ E3. Đi qua G3 không cho phép người thợ đẩy hộp ở B3 đến B1 → dẫn đến điểm chết. Vì vậy, công nhân đi qua lỗ E3 đến B2:

(2)

Cách đẩy duy nhất có thể thực hiện là A, ô B3 lên đến B4 (không phải đến B5 có nghĩa là điểm chết), hoặc ô C2 ở bên phải.

Chúng tôi nhận thấy rằng các hộp không thể được di chuyển đến các dấu chấm trên tuyến đường qua G3 vì chúng không bao giờ có thể được di chuyển sang bên trái sau đó, như đã thấy trong 1.2.

Nhưng để di chuyển chúng qua lỗ B3, C3, chúng ta cần không gian trong khu vực này, vì vậy chúng ta cần phải đặt một hoặc hai hộp bên phải và phải lấy chúng trở lại sau đó.

Chúng tôi cũng nhận ra rằng ô B3 chỉ có thể được di chuyển trên dòng B và do đó cuối cùng sẽ phải kết thúc trên chấm B4.

Để di chuyển các ô sau đó trên C4 và sau đó để đẩy chúng sang phải, công nhân phải có khả năng di chuyển đến A4 nhưng để đến đó từ bên dưới, ô B3 phải ở B2 và các khoảng trống B3, C3, C2 phải trống, vì vậy hai hộp phải ra khỏi đường và được đặt ở phía dưới bên phải.

(3)

nhưng việc đẩy hộp A3 hoặc B3 xuống không khả thi. Lựa chọn duy nhất còn lại mà chúng ta có ở vị trí 2 là đẩy hộp B3 lên B4 trước và sau đó thực hiện các động tác dẫn đến vị trí 3. Chúng ta nhận được

(4)

Bây giờ chúng ta có thể tiếp tục bằng cách đẩy hộp C3 xuống C2 và di chuyển công nhân xung quanh để đẩy hộp F2 đến G2 và G3:

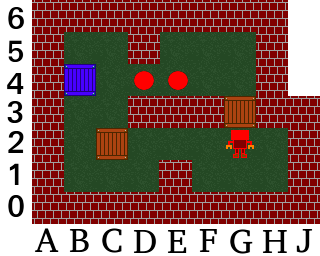(5)

Như đã thảo luận ở trên, chúng ta cần khoảng trống B3, C3, C2 và đưa hộp B4 xuống B2 nên chúng ta cần tạm thời đậu hộp C2 trên G2. Chúng ta có:

(6)

Bây giờ chúng ta có thể làm theo kế hoạch trước đó của mình và đẩy hộp G2 đến C4 để đẩy nó xa hơn về bên phải:

(7)

Câu hỏi là chúng ta phải đẩy hộp C4 đó đi bao xa. Vì chúng ta vẫn cần đẩy hộp G3 qua cùng một con đường nên chúng ta cần đưa thợ đến G4 và để làm điều đó, chúng ta cần đẩy hộp C4 ra xa F4 và di chuyển người thợ đến G4 để đẩy G4 đến G3:

(8)

Để chuyển hộp G2 sang trái người thợ cần phải quay lại theo hướng ngược chiều kim đồng hồ đối với hộp H2.

(9)

Phần còn lại rất đơn giản: hộp G2 được đẩy đến C2, C4, D4

(10)

sau đó hộp B2 được đẩy đến B4 và sau đó người thợ chuyển sang G4 để hoàn thành đẩy hộp F4 trên chấm E4.

HOÀN THÀNH.

¹ Giải thích về đệ quy:
Một người nào đó bị phá sản nếu người đó sở hữu tiền của người khác và không có tiền mặt và không có biên lai vì đã vay tiền của người khác hoặc có biên lai vì đã vay ai đó khác tiền nhưng người đó bị phá sản.

Giải thích về từ phá sản này sử dụng từ phá sản, và do đó nó được gọi là đệ quy.

Ví dụ:
Người A,B,C không có tiền, tất cả đều nợ người D,
A có biên lai vay tiền từ B,
B có biên lai vay tiền từ C,
C có biên lai vay tiền từ A
nhưng họ như một nhóm phá sản, mỗi người trong số họ.

Tương tự nhưng với một tình huống khác:
Người A, B, C không có tiền, tất cả đều nợ người D một số tiền,
A có biên lai vay tiền từ B,
B có biên lai vay tiền từ C,
C có biên lai vay tiền từ F,
Bởi vì người F có thể có tiền, có thể không ai trong số A,B,C bị phá sản.

Để phân biệt giữa hai trường hợp, người ta cần xem xét tất cả các mối quan hệ, không chỉ một mối quan hệ riêng lẻ bởi vì định nghĩa trên về phá sản là đệ quy.