Caribou in Covid: Contests are running online as usual. Check out the FAQ for further questions.
300000
English | Français | فارسی | 中文 | Українська | Azerbaijani | ខ្មែរ
How To Play
- To win, move the yellow block to the exit.
- To move a block, click and drag it, or click the block then click on the empty space.
- Grey blocks cannot be moved.
Puzzles shown on this page are created and owned by Caribou Contests ©
Comment Jouer
- L’objectif est de sortir le bloc jaune du plateau.
- Pour déplacer un bloc, il suffit de cliquer là-dessus et de le faire glisser. Vous pouvez aussi cliquer sur le bloc et ensuite cliquer sur l’espace vide adjacent.
- Les blocs gris ne peuvent pas être déplacés.
Les casse-têtes qui figurent sur cette page sont les créations et la propriété des Concours Caribou ©
玩法
- 将黄色方块移动到出口者获胜。
- 移动方块时，单击并拖拽，或在点击方块后点击空白位置。
- 不可以移动灰色方块。
这个页面的拼图是Caribou Contests的，同时也是他设计的。
چگونگی بازی
- برای برنده شدن، قطعه زرد را به سمت خروج حركت دهيد
- برای حرکت دادن یک بلوک، بر روی آن کلیک کنید و آن را بکشید، و یا اینکه بر روی بلوک و سپس روی فضای خالی کلیک کنید.
- بلوک های طوسی نمی توانند حرکت کنند.
تمامي پازل هاي نشان داده شده در اين صفحه ، ساخته شده و متعلق به Caribou Contests است
Editor Instructions
- Select a colour below the board to choose what colour block you wish to put on the board.
- Click on the board to place a single block of that colour.
- Click and drag on the board to enlarge the size of a block.
- Click the 'Clear Board' button to clear your board and start over.
- Use the width and height labels to change the size of your board.
- Click 'Generate Random Board' to randomly create a puzzle to edit.
- Click the 'Play Your Puzzle' button when you wish to play your board.
- Click 'Discard Your Puzzle' to cancel editing and return to the normal game.
Éditeur : Mode d’Emploi
- Sélectionnez une couleur sous le plateau pour choisir quelle sorte de bloc vous voulez poser sur le plateau.
- Cliquez sur le plateau pour y poser un seul bloc de la couleur sélectionnée.
- Cliquez et faites glisser votre curseur pour élargir le bloc.
- Cliquez sur le bouton ‘Effacer’ pour effacer le plateau et recommencer.
- Redimensionnez le plateau en modifiant les valeurs de Longueur et Largeur.
- Cliquez sur ‘Générer un Plateau Aléatoire’ pour générer un casse-tête aléatoire à modifier.
- Cliquez sur ‘Jouer à votre Casse-Tête’ quand vous voulez jouer le plateau créé.
- Cliquez sur ‘Abandonner votre Casse-Tête’ pour annuler vos modifications et retourner au jeu normal.
编辑指令
- 从以下面板选择你想要的颜色，该颜色即为你想要放在面板上的方块的颜色。
- 单击面板上的颜色以给一个方块着色。
- 单击并拖拽面板来放大方块。
- 单击“清除面板”重新开始。
- 使用宽度和高度标示来调整面板的大小。
- 单击“生成随机面板”来新建拼图。
- 单击“绘制拼图”来操作面板。
- 单击“放弃当前拼图”来取消编辑并回到常规界面。
دستورالعمل های تغییر دهنده
- برای انتخاب رنگ بلوکی که می خواهید در صفحه قرار دهید، یکی از رنگ های زیر صفحه را انتخاب کنید.
- برای قرار دادن یک بلوک از آن رنگ، بر روی صفحه کلیک کنید.
- برای بزرگ کردن اندازه ی یک بلوک، بر روی صفحه کلیک کنید و آن را بکشید.
- برای پاک کردن صفحه و شروع دوباره، بر روی کلید تمیز کردن صفحه کلیک کنید.
- برای تغییر اندازه ی صفحه تان، از برچسب های عرض و ارتفاع استفاده کنید.
- برای ایجاد یک صفحه ی تصادفی برای تغییر دادن، بر روی ایجاد صفحه ی تصادفی کلیک کنید.
- زمانی که می خواهید روی صفحه ی خودتان بازی کنید، بر روی کلید بازی کردن صفحه ی خود کلیک کنید.
- برای لغو کردن تغییرات و بازگشت به حالت بازی نرمال، بر روی لغو پازل خود کلیک کنید.
0
273094192012
You get the most out of the activities by first thinking for a while before expanding the answers to the questions.
Have fun.
After playing Sliding Blocks for a while, which one of our other games is similar to it?
- The Sokoban game is similar to Sliding Blocks for several reasons.
-
Which similarities do you see?
- In both games:
- Something has to be moved around, and the problem is a lack of empty space.
- Solution sequences may be long.
- The search tree is narrow. What that means is that if one makes random moves without a plan then one soon gets back to a position that one has encountered before. This makes these puzzles much easier than, for example, a Rubik's Cube, where random moves will basically never take you back to the starting position.
- It is useful to formulate intermediate goals. More about that further below.
How can one modify a Sliding Blocks puzzle to become easier or harder?
- To modify a problem one can click 'Create a Puzzle'. A puzzle becomes easier if blocks are replaced by empty space, or if larger blocks are split into smaller blocks occupying the same space, or if fixed grey blocks are changed into blue blocks to become movable. Equally, a puzzle becomes harder if empty space becomes occupied by a new block, or if small blocks are merged into bigger ones, or a blue block is changed into a grey block.
When watching animated solutions of puzzles, can you observe a general principle that these solutions have in common which might be a good hint for your own solution attempts?
- One hint is given next.
When it becomes harder to turn a key in a lock, or when the chain of your bicycle becomes stiff, what do you do?
- You can apply oil or grease to reduce friction.
In Sliding Blocks we also want to move blocks around and seem to encounter some kind of friction. Is there similar help here?
- The role of grease is played here by small blocks. It is a good idea to have 2 or sometimes 3 small blocks in between two larger blocks, especially around the yellow block which needs to be moved most. Here is the justification.
- Let us assume that the yellow block is two small squares wide and needs to be moved downwards.
- Then before the move there must be two empty spaces underneath the block, and after the move there will be two empty spaces where the block used to be. Then the two empty spaces above the yellow block need to move again around the yellow block so that this block can move further. To move the two spaces around the yellow block, the surrounding blocks need to be movable. Small blocks are easier to move than bigger ones, for example, around corners. Therefore it is a good idea to have groups of 2 and sometimes 3 small blocks between larger blocks, especially around the yellow block which needs to move most.
- Have a look at solutions of hard problems and check how often the above recommendation applies.
To find long solution sequences it is useful to think in terms of short sequences like building blocks out of which longer sequences are composed. One typical task of such a short sequence is to rotate blocks in a circle. Can you think how that is done?
- As an example, consider the following position:
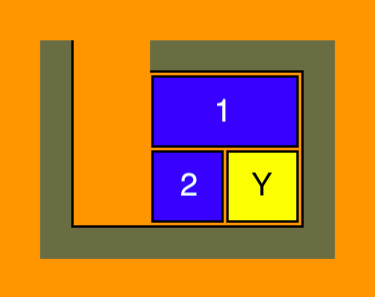
- The blocks 1, 2 and Y, and two free spaces can be moved around in a circle, and thus the block 1 or the two free spaces can be placed wherever they are needed.
- The next position has two larger blocks 1 and 3, but also more space:
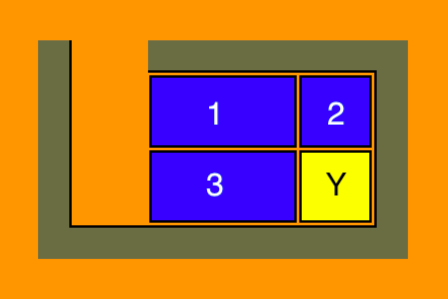
- Here all blocks can be moved in a circle as well, which allows us to position the blocks 1, 3 and the empty space wherever they are needed.
- Both circular motions will be needed in an example described further below.
Are there only blue and yellow blocks to be moved around?
- Strictly speaking, yes. But in science it is good to be flexible and inventive. How about considering empty spaces also as blocks which have the special ability that they can swap places with neighbouring blocks? For example, in solid state physics, missing electrons in a grid of atoms leave a gap and such a gap moves like a real particle just with opposite charge. Thinking this way makes it easier to explain, for example, how a transistor works.
- In our game the two circular motions of blocks mentioned in the previous item can also be seen as circular motion of the two empty spaces in the opposite direction.
If Sokoban and Sliding Blocks are similar, then which solving strategies of Sokoban can be used in Sliding Blocks?
- Because in both games the search tree is narrow, it is possible in both games to break up the whole solution into intermediate goals. For example, consider the following puzzle:
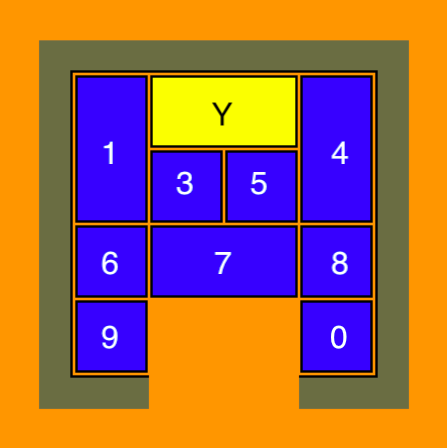
- The yellow wide block Y must pass the wide block 7 in order to get out. How should that be possible? For Y to move downwards we need small blocks around Y so that after moving Y the first time the empty space above Y can be moved below Y so that Y can be moved down further. Therefore two small blocks should be brought between Y and either block 1 or block 4, and then free space needs to be made underneath Y. Y is then moved downwards and the 2 small blocks should be moved to the new free space above Y.
- Before all of that, 1 or 4 must therefore be moved downwards. Let's go with 1. To move 1 down, the blocks 6 and 9 must be moved out of the way. According to our earlier hint to have small blocks close to the yellow block, we should start by moving 7 down, 6 and 9 into the new free space above 7 and then move 1 down and now rotate Y and 3 and 5 in a circle as described earlier so that Y and 3,5 swap places. After all of this we should have the resulting position:
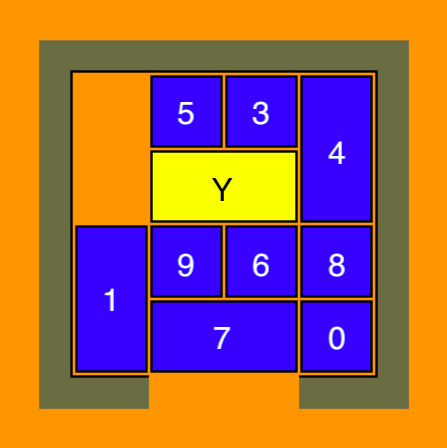
- Now we can either move 1 up, or we can move 5,3 and Y to the left, and move other blocks up on the right. Because it is always harder to pass larger blocks along each other, we should take the opportunity to move 1 up. What is left to do is to get 9,6 to the left to move Y down, to move 3 underneath 5, and 4 to the left to get 8,0 up. Now the 'building block rotation' described above is used to get Y above the exit. The puzzle is solved.
思考后再展开你的回答即可完成大部分练习。
玩得开心！
在尝试过滑动方块后，你觉得我们的那一款游戏和它很相像？
- Sokoban和滑动方块有很多相似之处。
-
你觉得哪些地方相似呢？
- （哪些点）在两个游戏里都出现过？
- 你必须要移动一些东西，而在这过程中最主要的问题就是没有足够的空白位置。
- 解决问题的方式可能会很长。
- 查找树的范围很窄，这意味着随意移动时你可以回到你原先发掘的位置。这使这些拼图比一般的简单，比如说移动后无法让你回归原位的Rubik’s Cube。
- 制定中间方案很很有用。详情如下。
如何改变滑动方块使其变得更简单或更难？
- 单击“新建拼图”来解决问题。在这些情况下拼图会变得更简单：用空白替代滑块，将大滑块分割成几个小滑块并占据原有的面积，或者将灰色滑块变成蓝色使其可被移动。同样的，为了提升拼图难度，可使滑块占据原有的空白位置，或者将小滑块合并成大滑块，使蓝色滑块变成灰色而不能被移动。
观看解拼图动画的过程中你能总结出什么共同点？这个（这些）共同点有利于你自己的解题过程。
- 接下来有个提示。
当你很难把钥匙插进锁里，或者你的自行车链条生锈动不了的时候，你会怎么做》
- 你可以添加润滑油来减小摩擦。
在滑动方块中你想移动方块，但是你发现游戏中也会遇到这样的阻力。这两点有什么相似之处吗？
- 小方块在这里起到的就是润滑作用。在两个大滑块中间放置2-3个小滑块，尤其是最需要被移动的黄色方块周围。以下是理解分析。
- 假设黄色方块有两个小方块宽，现在我们需要把它往下移。
- 在此之前它下面需要有两个空白位置，而在移动后仍会有两个。移动后黄色方块上方的两个空白位置需要跟随黄色方块以使其移动得更远，所以黄色方块周围的方块是需要可以被移动的。小方块比大方块更容易移动，例如它们在角落的时候。因此在两个大滑块中间放置2-3个小滑块是很有用的，尤其是最需要被移动的黄色方块周围。
- 在看完难题的解决方时候，想想你是不是会经常有这样的思路。
在解决长问题时，我们可以把它分成很多小问题由此拼接推断出过程。其中很典型的一个问题就是旋转滑块。你觉得如何做到这一点呢？
- 思考以下情境：
- 滑块1，2 ，Y以及两个空白位置是可以旋转移动的，因此滑块1和两个空白位置可以放到任意需要的地方。
- 接下来剩下两个大滑块1和3，但同时也有更多的空白位置。
- 在这种情况下所有的滑块都可以旋转移动，所以我们可以将滑块1，3以及空白位置放到我们需要的地方。
- 以下例子可以描述这两个旋转移动。
只有蓝色和黄色滑块可以到处移动吗？
- 严格意义上来说是的。但在科学上来说灵活和有创意总是好的。这时候不如把空白位置想像成滑块，而这些是具有特殊能力的，因为它们可以和周围的滑块交换位置。举例来说，在物理中，原子中缺失的电子创造了空白位置，而这些空白的部分像粒子一样移动，只是带有相反电荷。 由此分析就变得简单了，比如这样就可以想象晶体管是如何工作的。
- 在我们的游戏中滑块的两个旋转运动就可以看作是两个空白位置做反向旋转运动。
如果Sokoban和滑块很相似，那么Sokoban的哪些玩法可以被运用到滑块里？
- 因为在两个游戏中查找树都很窄，因此两个游戏的解决方式都可以被拆分成一步一步的目标。例如看这个拼图：
- 黄色的宽方块Y需要通过黄色方块7的位置来移动到外面去。如何达到呢？为了使Y向下移动我们需要在它的周围放置小滑块，在Y第一次移动后，Y上方的空白位置可以移动到Y下方，由此Y可以移动得更远。 因此在Y和滑块1或4之间需要放置两个小滑块，而Y的下方需要空白位置。在Y向下移动后，两个小滑块需要挪到Y上方新出现的空白位置去。
- 在此之前，滑块1或4需要向下移动。在这个例子中我们只考虑1。为了向下移动1，滑块6和9需要被移开。 在我们之前的提示中提到了黄色方块周围需要小滑块这一点，所以我们开始时先向下移动7，而6和9挪到7上方的新空白。此时向下移动1，用之前提到的方式旋转Y，3和5。在此之后我们得到了以下布局“
- 现在我们可以向上移动1，或者把Y，3和5移到左边去，然后将其他滑块上移到右边。 因为大滑块总是更难一起移动，我们需要利用1可以移动的机会。剩下的就是左移6和9，这样Y就可以下移， 3在5的下方，而4则被用来上移8和0. 这样滑块旋转就完成了，Y可以被移动到出口，拼图完成。
Pour profiter au mieux des activités, il est préférable de réfléchir par vous-même avant de dévoiler les réponses.
Amusez-vous!
Après avoir joué à Sliding Blocks pendant un bon moment, à quel autre jeu de notre site ressemble-t-il?
- Le jeu Sokoban ressemble à Sliding Blocks.
-
Quelles similitudes avez-vous relevées entre ces deux jeux?
- Dans les deux jeux:
- Il faut déplacer quelque chose, et le problème est le manque d’espace vide.
- Les séquences de solution peuvent être longues.
- L’arbre de recherche est ‘étroit’, ce qui signifie que si on joue des coups au hasard sans stratégie, on revient sous peu à une position qu’on a déjà rencontrée. Du coup, c’est ce qui rend ces casse-têtes plus faciles qu’un Rubik’s cube, où il est alors très improbable de retrouver la position de départ en effectuant des coups au hasard.
- Il est utile de se fixer des objectifs intermédiaires, qu’on abordera plus tard dans le texte ci-dessous.
Comment peut-on modifier un casse-tête Sliding Blocks pour le rendre plus facile ou plus difficile?
- Pour modifier un casse-tête, on peut cliquer sur ‘Modifier le Plateau Actuel’. Un casse-tête devient plus facile si on remplace des blocs par de l’espace vide, si on remplace un grand bloc par de plus petits blocs occupant la même place, et si on remplace des blocs gris fixes par des blocs bleus qu’on peut déplacer. De même, un casse-tête devient plus difficile si on réduit l’espace vide en plaçant des blocs, si on combine des petits blocs pour former des blocs plus grands, et si on remplace un bloc bleu par un bloc gris.
En regardant des solutions animées des casse-têtes, observez-vous un principe de résolution général qui pourrait vous servir quand vous tentez de résoudre les casse-têtes?
- Un indice suivra.
Que faites-vous lorsqu’il devient difficile de tourner une clé dans une serrure, ou lorsque la chaîne de votre vélo se bloque?
- Vous pouvez lubrifiez avec de l’huile ou de la graisse pour réduire la friction.
Dans Sliding Blocks aussi on veut déplacer des blocs mais il semble qu’on rencontre une sorte de friction. Existe-t-il une solution pareille?
- Ici ce sont les petits blocs qui lubrifient. C’est une bonne idée de placer deux ou parfois 3 petits blocs entre deux grands blocs, spécialement autour du bloc jaune qui est le plus souvent déplacé. Voici la justification.
- Disons que le bloc jaune fait deux cases de largeur et qu’il faut le descendre sur le plateau.
- Alors, avant qu’on le déplace il faut deux cases vides en dessous, et après qu’on l’aura déplacé il y aura deux cases vides où se trouvait le bloc jaune avant. Ensuite, pour pouvoir descendre le bloc jaune de nouveau, il faut que ces cases vides se déplacent autour de lui. Pour déplacer les cases vides autour du bloc jaune, les blocs qui l’entourent doivent être mobiles. Il est plus facile de déplacer un petit bloc, autour d’un coin par exemple. Donc, c’est une bonne idée de faire en sorte qu’il y ait des groupes de 2 ou même 3 petits blocs entre les grands blocs, spécialement autour du bloc jaune qui est le plus souvent déplacé.
- Jetez un oeil à des solutions de problèmes difficiles et vérifier à quelle fréquence la recommandation ci-dessus est applicable.
Pour trouver de longues séquences de solution, il est utile de penser aux longues séquences comme étant composées de petites séquences. Souvent l’objet d’une telle petite séquence consiste à faire tourner des blocs dans un cercle. Pouvez-vous envisager cette action?
- Comme exemple, on peut considérer la position suivante:
- On peut faire tourner les blocs 1, 2, Y, et les deux cases vides dans un cercle, et ainsi placer le bloc 11 et les deux cases vides où il convient.
- La position suivante comprend deux blocs plus grands (1 et 3) mais plus de place aussi:
- Ici aussi on peut faire tourner tous les blocs dans un cercle, ce qui nous permet de placer les grands blocs et les cases vides où il convient.
- On aura besoin des deux mouvements circulaires décrits dans un exemple qui sera énoncé par la suite.
Est-ce que seuls les blocs bleus et jaunes sont mobiles?
- À proprement parler, oui. Pourtant, en sciences, il est bien d’avoir une souplesse et une ouverture d’esprit. Et si on considérait les cases vides comme des blocs qui ont la propriété spéciale de pouvoir échanger leur place avec celle des blocs avoisinants? Par exemple, dans le domaine de la physique de l’état solide, les électrons manquants dans une grille d’atomes laissent un vide et un tel vide se déplace comme une vraie particule mais de charge opposée. Penser ainsi peut rendre plus facile, par exemple, l’explication du fonctionnement d’un transistor.
- Dans notre jeu, on pourrait représenter les deux mouvements circulaires des blocs mentionnés ci-dessus comme le mouvement circulaire des cases vides dans le sens contraire.
Si Sokoban et Sliding Blocks se ressemblent, alors quelles stratégies de résolution applicables pour Sokoban peuvent servir dans Sliding Blocks?
- Du fait que l’arbre de recherche des deux jeux est étroit, il est donc possible de diviser la solution en plusieurs objectifs intermédiaires. Considérez le casse-tête suivant:
- Le grand bloc Y doit franchir le grand bloc 7 afin de sortir. Comment faire? Pour que Y puisse descendre, il faut qu’il y ait des petits blocs autour de lui: ainsi, une fois qu’on l’aura déplacé une première fois, on pourra déplacer l’espace vide au-dessus de lui en-dessous, pour pouvoir le descendre davantage. Alors on devrait faire en sorte qu’il y ait des petits blocs entre Y et un bloc (soit 1, soit 4) et ensuite qu’il y ait de l’espace vide sous lui. Ensuite on pourrait descendre Y et on devrait mettre les 2 petits blocs dans l’espace vide au-dessus de lui.
- Pour accomplir cela, il faut dans un premier temps faire descendre 1 ou 4. Procédons avec 1. Pour que 1 puisse descendre, il faut déplacer les blocs 6 et 9 de façon à ce qu’ils ne bloquent plus le chemin. En se rappelant de notre astuce qui dit qu’il est avantageux de mettre les petits blocs autour du bloc jaune, il faut d’abord faire descendre le bloc 7, placer les blocs 6 et 9 dans l’espace vide au-dessus de 7, ensuite faire descendre le bloc 11, puis faire tourner les blocs Y, 3, et 5 dans un cercle de sorte que Y échange sa place contre celles de 3 et 5. Cela accompli, la position résultante sera:
- Arrivé à cette étape, on peut soit faire monter le bloc 1, soit déplacer 5,3 et Y vers la gauche et déplacer les autres blocs placés du côté droit. On devrait utiliser l’opportunité de faire monter 1 car il est toujours plus difficile de manipuler deux grands blocs avoisinants. Tout ce qui nous resterait à faire, serait de déplacer 9,6 vers la gauche pour faire descendre Y, de déplacer 3 sous 5, et déplacer 4 vers la gauche pour pouvoir faire monter 8,0. À partir de là, on pourrait effectuer la rotation de blocs décrite ci-dessus pour placer Y au-dessus de la sortie. Le casse-tête est résolu.
با فکر کردن برای مدتی پیش از پاسخ دادن به سوال، شما دستاورد بیشتری خواهد داشت.
اوقات خوبی داشته باشید.
بعد از بازی کردن هل دادن بلوک ها برای مدتی، کدام یک از بازی های دیگر ما به این بازی شباهت دارد؟
- بازی سوکوبان به بازی هل دادن بلوک ها به دلایل زیادی شباهت دارد.
-
شما چه شباهت هایی می بینید؟
- در هر دو بازی:
- یک چیز باید در حرکت باشد، و مشکل کمبود فضای خالی است.
- دنباله های پاسخ ممکن است طولانی باشند.
- جستجوی درختی محدود است. این به این معنی است که اگرشخصی حرکت تصادفی بدون برنامه ریزی صورت دهد، آنگاه به سرعت به وضعیتی که قبلا با آن مواجه شده بود، بازگشت خواهد داشت. این مساله این پازل ها را بسیار آسان می کند، به عنوان مثال، یک مکعب روبیک، که حرکت های تصادفی اساسا هرگز شما را به کوقعیت ابتدایی بر نخواهد گرداند.
- این مفید است که هدف میانی را به صورت فرمول بیان کنید. در ادامه بیشتر در این رابطه مطرح خواهد شد.
چگونه می شود بازی هل دادن بلوک ها را تغییر داد به گونه ای که آسان تر یا سخت تر شود؟
- برای تغییر یک مساله می توان بر روی تغییر صفحه ی کنونی کلیک کرد. یک پازل آسان تر می شود اگر بلوک ها با فضای خالی جابجا شوند، یا اینکه بلوک های بزرگتر به بلوک های کوچکتر که فضای یکسانی را اشغال می کنند تقسیم شوند، و یا اینکه بلوک های طوسی ثابت به بلوک های آبی تغییر پیدا کنند که قابل حرکت دادن شوند. یه طور یکسان، پازل سخت تر میشود اگر که فضای خالی با بلوک های جدید اشغال شوند، یا اینکه بلوک های کوچک ترکیب شوند که بلوک های بزرگتر به وجود آیند، یا اینکه بلوک های آبی به بلوک های طوسی تغییر کنند.
در هنگام تماشای پاسخ های متحرک پازل ها، آیا می توانید یک اصل عمومی را نتیجه بگیرید که همه ی این پاسخ ها در آن مشترک هستند و ممکن است برای تلاش های شما برای پاسخ، راهنمایی خوبی باشد؟
- یک راهنمایی بعد از این داده شده است.
هنگامی که چرخاندن کلید در یک قفل سخت تر می شود، یا هنگامی که زنجیر دوچرخه ی شما به سختی گیر می کند، شما چخ می کنید؟
- شما می توانید روغن یا گریس به آن بزنید با اصطکاک را کاهش دهید.
در هل دادن بلوک ها ما همچنین می خواهیم که بلوک ها را حرکت دهیم و احتمالا با نوعی از اصطکاک مواجه شویم. آیا راهنمایی مشابهی وجود دارد؟
- نقش گریس در اینجا با بلوک های کوچک ایفا می شود. این ایده ی خوبی است که ۲ یا گاهی ۳ بلوک کوچک در بین دو بلوک بزرگتر داشته باشیم، مخصوصا در اطراف بلوک زرد که احتیاج دارد بیشتر حرکت داده شود. در اینجا دلیل آن را می بینید.
- اجازه دهید فرض کنیم که بلوک زرد با عرض دو مربع کوچک می باشد و لازم است که به سمت پایین حرکت داده شود.
- آنگاه قبل از حرکت باید دو فضای خالی در زیر بلوک ها وجود داشته باشد، و بعد از حرکت دو فضای خالی در جایی که بلوک ها قبلا بوده اند خواهند بود. آنگاه دو فضای خالی بالای بلوک زرد لازم است که دوباره در اطراف بلوک زرد حرکت داده شود به طوری که این بلوک بتواند جلوتر حرکت کند. برای حرکت دادن دو فضای اطراف بلوک زرد، بلوک های احاطه کننده ی آن لازم است که قابل جرکت باشند. بلوک های کوچک راحت تر از بلوک های بزرگ تر حرکت داده می شوند، به عنوان مثال، در اطراف گوشه ها. بنابراین این ایده ی خوبی است که گروه هایی از ۲ و یا گاهی ۳ بلوک کوچک در بین بلوک های بزرگ تر داشته باشیم، مخصوصا در اطراف بلوک زرد که لازم است که بیشتر از همه حرکت کند.
- به پاسخ های مسائل دشوار نگاهی داشته باشید و چک کنید که چه تعداد دفعات توصیه ی بالا اعمال می شود.
برای پیدا کردن دنباله های پاسخ طولانی این مفید است که در غالب دنباله های کوتاه مثل بلوک های ساختمان که بیرون از آن دنباله های بلند تر ترکیب شده اند، فکر شود.
یک کار خاص از این نوع دنباله ی کوتاه این است که بلوک ها را در یک دایره بچرخانیم.
می توانید به این فکر کنید که چطور چنین مساله ای انجام پذیر است؟
- به عنوان مثال، موفعیت زیر را در نظر بگیرید:
- بلوک های ۱و ۲و Y، و دو فضای خالی می توانند در اطراف دایره گونه حرکت داده شوند، و بنابراین بلوک ۱ یا دو فضای خالی می توانند در هر جایی که لازم است فرار داده شوند.
- موقعیت بعدی دو بلوک بزرگتر ۱ و ۳ و همچنین فضای بیشتری دارد:
- در اینجا هم همه ی بلوک ها می توانند در یک دایره حرکت کنند، که به ما اجازه می دهد که بلوک های ۱، ۳ و فضای خالی را در هر جایی که لازم است قرار دهیم.
- هر دو حرکت دایره ای در مثالی که بعدا در زیر مطرح می شود لازم خواهند شد.
آیا فقط بلوک های آبی و زرد برای حرکت کردن در اطراف وجود دارند؟
- به بیانی دقیق تر، بله. اما در علم خوب است که انعطاف پذیر و نوآور باشید. چه می شود اگر فضاهای خالی را هم مثل بلوک ها در نظر بگیریم که قابلیت خاصی دارند که می توانند با بلوک های همسایه جابجا شوند؟ به عنوان مثال، در فیزیک حالت جامد، از دست دادن الکترون در یک حلقه از اتم ها یک فضای خالی به وجود می آورد و چنین فضای خالی ای مانند یک ذره ی واقعی اما فقط با بار مخالف حرکت می کند. با اینکونه فکر کردن توضیح آسانتر می شود، به عنوان مثال، اینکه یک ترانزیستور چگونه کار می کند.
- در بازی ما دو حرکت دایره ای بلوک ها که در مورد قبلی عنوان شد، می تواند همچنین به عنوان حرکت دایره ای دو فضای خالی در جهت های مخالف دیده شود.
اگر سوکوبان و هل دادن بلوک ها شبیه هم هستند، آنگاه کدام استراتژی حل سوکوبان می تواند در هل دادن بلوک ها استفاده شود؟
- از آنجایی که در هر دو بازی جستجوی درختی محدود است، در هر دو بازی این امکان وجود دارد که تمام پاسخ به دو هدف میانی تقسیم شود. به عنوان مثال، پازل زیر را در نظر بگیرید:
- بلوک عریض زرد Y باید برای بیرون رفتن از بلوک عریض ۷ بگذرد. چگونه همچین چیزی ممکن می شود؟ برای اینکه Y به سمت پایین حرکت کند ما به بلوک های کوچک در اطراف Y نیاز داریم به گونه ای که بعد از حرکت دادن Y برای بار اول، فضای خالی بالای Y می تواند به پایین Y حرکت داده شود به گونه ای که Y بعدا می تواند به پایین حرکت داده شود. بنابراین دو بلوک کوچک باید بین بلوک Y و بلوک ۱ با ۴ آورده شود، و آنگاه فضای خالی لازم است که در پایین Y به وجود آید. Y آنگاه به پایین حرکت داده می شود و ۲ بلوک کوچک باید به فضای خالی جدیدی بالای Y حرکت داده شوند.
- قبل از همه ی آنها، ۱ و ۴ باید در نتیجه به پایین حرکت داده شوند. بیایید با ۱ شروع کنیم. برای پایین حرکت دادن ۱، بلوک های ۶ و ۹ باید از سر راه حرکت داده شوند. بر اساس راهنمایی قبلی ما برای داشتن بلوک های کوچک در نزدیکی بلوک زرد، ما باید با حرکت دادن ۷ به پایین، ۶ و ۹ به فضای خالی بالای ۷ و آنگاه حرکت دادن ۱ به پایین و حالا چرخاندن Y و ۳ و ۵ در یک دایره به همان شکل که قبلا توضیح داده شد به گونه ای که Y و ۳ و ۵ جایشان با هم عوض شود. بعد از همه ی اینها ما باید موقعیت به دست آمده را داشته باشیم:
- اکنون می توانیم یا ۱ را به بالا حرکت دهیم، با ۳و۵ و Y به چپ، و بقیه بلوک ها بالا به راست. زیرا که این همیشه دشوار تر است که از بلوک های یزرگتر در کنار هم گذشت، ما باید از این فرصت استفاده کنیم که ۱ را به بالا حرکت دهیم. کاری که باقیمانده است تا انجام دهیم این است که ۹، ۶ را به چپ برده تا Y را به پایین حرکت دهیم، برای حرکت ۳ به زیر ۵، و ۴ به چپ برای بردن ۸، ۰ به بالا. اکنون چرخش بلوک ساختمان توضیح داده شده در بالا استفاده میشود تا Y را به بالا برای خروج حرکت دهیم. پازل حل شده است.
Follow or subscribe for updates: