300000
English | Français | فارسی | 中文 | Українська | Azerbaijani | ខ្មែរ | Tiếng Việt | Bahasa Melayu | Deutsch | O'zbek | РусскийSliding Blocks ©©
游戏次数: 426408
胜局数: 314602
胜局数: 314602
怎么玩
- 移动黄色滑块到出口处，你才能获胜
- 点击并拖拽移动滑块，或者先点击方块再点击空白区域
- 灰色滑块不能被移动
这个页面的题板由Caribou Contests©设计并所有。
编辑指令
- 使用宽度和高度标示来调整题板的大小。
- 从下面选择你想要的颜色，该颜色即为你想要放在题板上的滑块颜色。
- 单击面板上的颜色以给一个滑块着色。
- 单击并拖拽面板来放大滑块。
- 单击“清除题板”重新开始。
- 单击“生成随机题板”来新建拼图。
- 单击“绘制拼图”来操作题板。
- 单击“放弃当前题板”来取消编辑并回到常规界面。
移动步数：0
宽高
难度： 简单 中等 难 非常难 终极难题
慢速快速
思考后再展开你的回答即可完成大部分练习。
玩得开心！
在尝试过Sliding Blocks后，你觉得我们的那一款游戏和它很相像？
- Sokoban和Sliding Blocks有很多相似之处。
-
你觉得哪些地方相似呢？
- （哪些点）在两个游戏里都出现过？
-
- 你必须要移动一些东西，而在这过程中最主要的问题就是没有足够的空白位置。
- 解决问题的方式可能会很长。
- 查找树的范围很窄，这意味着随意移动时你可以回到你原先发掘的位置。这使这些拼图比一般的简单，比如说移动后无法让你回归原位的Rubik’s Cube。
- 制定中间方案很很有用。详情如下。
如何改变Sliding Blocks使其变得更简单或更难？
- 单击“新建题板”来解决问题。在这些情况下题板会变得更简单：用空白替代滑块，将大滑块分割成几个小滑块并占据原有的面积，或者将灰色滑块变成蓝色使其可被移动。同样的，为了提升拼图难度，可使滑块占据原有的空白位置，或者将小滑块合并成大滑块，使蓝色滑块变成灰色而不能被移动。
观看解拼图动画的过程中你能总结出什么共同点？这个（这些）共同点有利于你自己的解题过程。
- 接下来有个提示。
当你很难把钥匙插进锁里，或者你的自行车链条生锈动不了的时候，你会怎么做？
- 你可以添加润滑油来减小摩擦。
在Sliding Blocks中你想移动滑块，但是你发现游戏中也会遇到这样的阻力。这两点有什么相似之处吗？
- 小滑块在这里起到的就是润滑作用。在两个大滑块中间放置2-3个小滑块，尤其是最需要被移动的黄色滑块周围。以下是理解分析。
- 假设黄色滑块有两个小滑块宽，现在我们需要把它往下移。
- 在此之前它下面需要有两个空白位置，而在移动后仍会有两个。移动后黄色滑块上方的两个空白位置需要跟随黄色滑块以使其移动得更远，所以黄色滑块周围的滑块是需要可以被移动的。小滑块比大滑块更容易移动，例如它们在角落的时候。因此在两个大滑块中间放置2-3个小滑块是很有用的，尤其是最需要被移动的黄色滑块周围。
- 在看完难题的解决方时候，想想你是不是会经常有这样的思路。
在解决长问题时，我们可以把它分成很多小问题由此拼接推断出过程。其中很典型的一个问题就是旋转滑块。你觉得如何做到这一点呢？
- 思考以下情境：
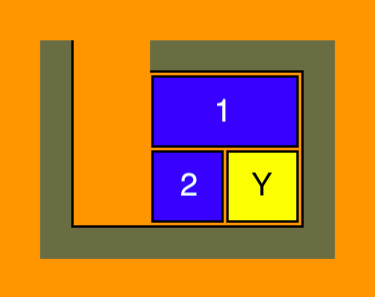
- 滑块1，2 ，Y以及两个空白位置是可以旋转移动的，因此滑块1和两个空白位置可以放到任意需要的地方。
- 接下来剩下两个大滑块1和3，但同时也有更多的空白位置。
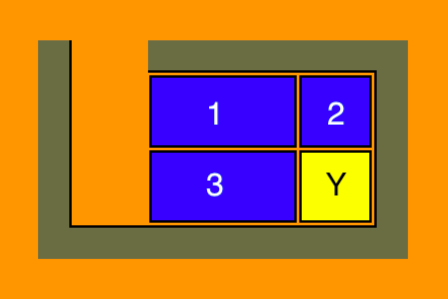
- 在这种情况下所有的滑块都可以旋转移动，所以我们可以将滑块1，3以及空白位置放到我们需要的地方。
- 以下例子可以描述这两个旋转移动。
只有蓝色和黄色滑块可以到处移动吗？
- 严格意义上来说是的。但在科学上来说灵活和有创意总是好的。这时候不如把空白位置想像成滑块，而这些是具有特殊能力的，因为它们可以和周围的滑块交换位置。举例来说，在物理中，原子中缺失的电子创造了空白位置，而这些空白的部分像粒子一样移动，只是带有相反电荷。 由此分析就变得简单了，比如这样就可以想象晶体管是如何工作的。
- 在我们的游戏中滑块的两个旋转运动就可以看作是两个空白位置做反向旋转运动。
如果Sokoban和Sliding Blocks很相似，那么Sokoban的哪些玩法可以被运用到Sliding Blocks里？
- 因为在两个游戏中查找树都很窄，因此两个游戏的解决方式都可以被拆分成一步一步的目标。例如看这个拼图：
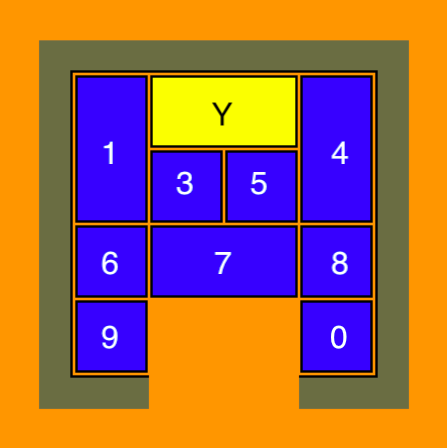
- 黄色的宽滑块Y需要通过黄色滑块7的位置来移动到外面去。如何达到呢？为了使Y向下移动我们需要在它的周围放置小滑块，在Y第一次移动后，Y上方的空白位置可以移动到Y下方，由此Y可以移动得更远。 因此在Y和滑块1或4之间需要放置两个小滑块，而Y的下方需要空白位置。在Y向下移动后，两个小滑块需要挪到Y上方新出现的空白位置去。
- 在此之前，滑块1或4需要向下移动。在这个例子中我们只考虑1。为了向下移动1，滑块6和9需要被移开。 在我们之前的提示中提到了黄色方块周围需要小滑块这一点，所以我们开始时先向下移动7，而6和9挪到7上方的新空白。此时向下移动1，用之前提到的方式旋转Y，3和5。在此之后我们得到了以下布局“
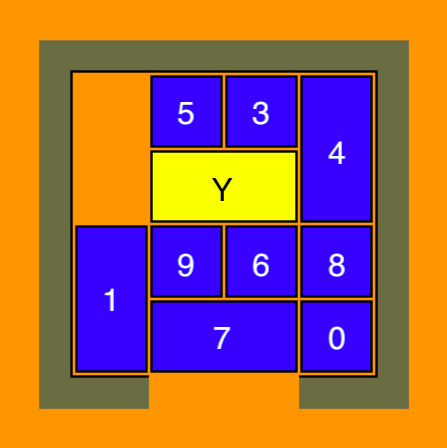
- 现在我们可以向上移动1，或者把Y，3和5移到左边去，然后将其他滑块上移到右边。 因为大滑块总是更难一起移动，我们需要利用1可以移动的机会。剩下的就是左移6和9，这样Y就可以下移， 3在5的下方，而4则被用来上移8和0. 这样滑块旋转就完成了，Y可以被移动到出口，拼图完成。
摘要
- 作为一个一般策略，从最终的目标，即把黄色滑块弄出来开始，然后向后倒推，制定必要的子、子、子......目标，这些目标共同展示了整个解决方案。
- 把大滑块移开，最好是移到离出口很远的角落。
- 很容易发现，有些滑块太大，无法相互通过。通过意识到这种移动的局限性，可以避免猜测，避免无结果的尝试，更好地制定子目标。
- 为了继续移动一个更大的滑块，需要在滑块块前面创建空位，然后移动滑块，这导致滑块后面出现空位。这些产生的空位需要被"移动 "到大滑块的前面，以进一步移动大滑块。所有这些移动都需要在大滑块之前和之后有小滑块。因此，第一个移动序列可能只是为了把小滑块放在以后需要的地方，即大滑块周围。
- 要移动一个大的滑块，需要在它要移动的方向上有一定的空间。例如，如果该滑块在一个方向上的宽度为2，但是整个题板只有一个空位，那么该滑块将永远无法在这个方向上移动，但是可以在与之垂直的方向上移动，因为那里更窄。同样的，如果一个题板只有2个空位，而一个滑块的宽度是3，那么这个滑块将永远无法在这个宽度的垂直方向上移动，因为这需要3个空位。但是这个滑块可以向另一个方向移动。同样，知道有限的可移动性可以使我们更容易找到解决方案，因为我们知道每个大滑块只能向哪个方向移动，并且只考虑这种移动。
- 在一个圆圈中，一个或两个空位与圆圈中的所有方框一起被移动，"发现"这个圆圈是很有用的。这样的圆圈可以有一个长方形的形状。在圆圈中移动所有的东西（空位和方框）并不触及圆圈外的任何其他滑块，可能看起来毫无意义。但是，将小滑块带到圆圈中的某个位置，其副作用可能会在以后起到关键作用。一个例子是靠近一个大滑块的地方，以便在这个滑块被移动后填满空位。用圆圈这样的移动序列来思考，而不是用单一的移动来思考，可以让人想得更深。
- 一个推荐的学习策略是，从简单的题板开始，慢慢增加难度。如果一个人不能解决一个题板，那么他就会观看动画解决方案，找到自己错过的那一步，通过观察接下来的移动来思考这一步的目的，以及如何才能看到这个目的。
关注或订阅更新：