You might be familiar with knots in your every day life. When you tie your shoelaces or pull headphones out of your pocket, you are encountering knots. If you can find one loose end of the knot, you can simply pull the loose end through the entire knot until it is completely unravelled.
What happens if you glue the two loose ends together? How much can you untangle the knot now? This is the kind of question that mathematicians like to study in the field of knot theory. Mathematicians think of knots as being one big loop. You can make it by taking a circle, cutting it in one place, tying the knot up, and gluing the ends back together.
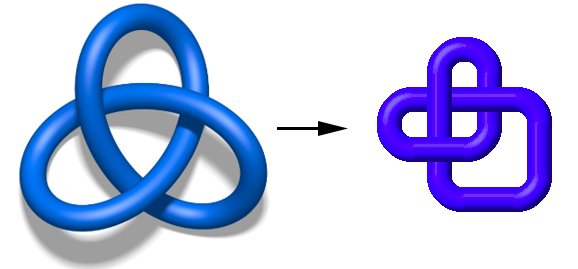
The images below are diagrams of the first few knots you can get using the procedure of cutting a circle, tying it up, then gluing the ends back together.

The field of topology in mathematics involves studying how things are connected to each other (even when they are stretched or deformed, lengths do not matter). For example, if you start at any point on the circle, you can always go to a neighbouring point on the circle. If you go one direction all the way around the circle, you come back to where you started. If we think about the circle as just having these properties (without the roundness, or needing to draw it somewhere on a piece of paper), we are talking about $S^1$, the "1-sphere". If you think about it, our knot is kind of like $S^1$ because we can start anywhere on the knot and go around it to eventually come back to where we started. One way of constructing $S^1$ is to take the number line between 0 and 1 and cut it out so you get a small segment of line. Then, take the points corresponding to 0 and to 1, and glue them together to make a loop whose total circumference is 1.
What makes our knots different from $S^1$ is that they are sitting in 3-dimensional space while $S^1$ is not. Mathematicians describe a way of taking every point on our original circle and sending them to some point in 3D space that preserves the way the circle is connected an embedding of the circle. If we call this embedding $h$ then we write this down as $$ h: S^1 \to \mathbb{R}^3 $$ Which we can read as ``$h$ is defined as ($:$) a function ($\to$) that associates points on a circle ($S^1$) to points in 3D (Euclidian) space ($\mathbb{R}^3$).
Imagine a loop of rope with no knots in it. Mathematicians refer to this knot as the unknot. What happens if you take this knot and tangle it with itself, without cutting or gluing? It might look like a completely different knot. However, if you are careful, you will still be able to untangle it back to its original state. This is true for any knot: you can tangle it up or untangle it, and even though it looks completely different, it is still the same knot. The problem of trying to identify which knots are the same knot is a hard problem for mathematicians in practice. Two knots might look completely different but actually be the same knot. For example, the knot diagram below represents an unknot. Try Tools > Simplify to see the simplified version of the knot.
If we are thinking about a representation of a knot in 3D (let's call it $K_0$), we say that it is equivalent to another knot $K_1$ if there is an ambient isotopy between them. This is a fancy way of saying "deformation", but it carries with it some special rules.
The "ambient" part means that we are doing all of our deformations in 3D space (i.e., we can't cheat by going down to 2D and squishing away a part of the knot, or by going to 4D and untangling the knot with an extra dimension).
The "isotopy" part means we are doing our deformations continuously, without letting the knot pass through itself. One way to think of a continuous deformation is to have it start at some time $t = 0$, where the knot looks like $K_0$, and finish at some time $t=1$, where the knot looks like $K_1$. Then we can "zoom in" on very small time steps (for example, $t = 0.5442$ to $t = 0.5443$), and we will see corresponding very small changes in the knot $K_{0.5442} \to K_{0.5443}$.Another reason it's important to stay in 3D space is to prevent us from doing things like squishing part of the knot down into a single point or line in a lower dimension, which could make the knot again very easy to untangle.
While a knot is really a 3D structure, we tend to look at things in 2D (paper, screens, etc). If we are careful, we can draw a diagram for a knot with all of the information about the original 3D knot. If we imagine shining a light onto a knot and looking at its shadow, it would look like a a squiggly line. The places where this line overlaps itself is called a crossing.
Crossings show up when we project our 3D knot onto a 2D diagram. If two pieces of our loop are on top of each other, they form a crossing. In our actual 3D knot, we can imagine which part of the knot is "on top" of the other. When we draw crossings in the 2D diagram, we need a way of "remembering" which part of the knot was on top of the other. In this module, we use special graphics to give our knots a 3D look, while still making it obvious which strand is on top and which is underneath. At the crossing, the section of the knot that goes 'on top' is called a overpass, while the section that goes underneath is called an underpass.
Something to keep in mind when looking at knot diagrams is that there are infinitely many knot diagrams for any one knot. These knot diagrams might look completely different from one another, but they all represent the same mathematical knot.
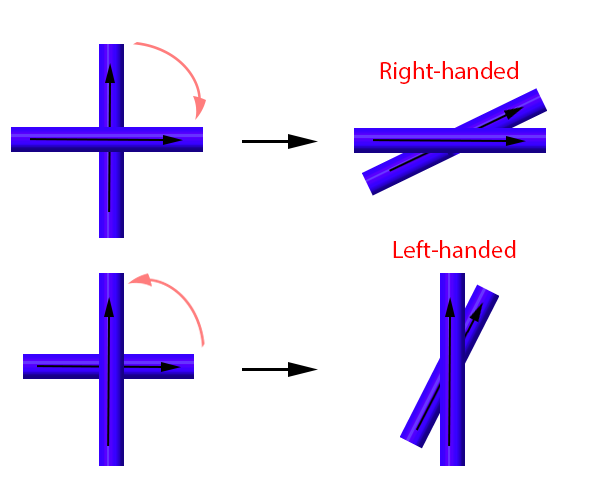
Crossings come in two flavours: right-handed and left-handed . Recall how we chose a direction to walk along our loop? Imagine we do this, keeping track of the direction that we walk at each crossing. At each crossing, the overpass and the underpass will both have directions. If we just think about the crossing and the direction of each path at the crossing, we can think of each crossing as being a pair of overlapped arrows.

No matter how these arrows point at a crossing, they must both lie on one side of the crossing (try it yourself!).

If we can wiggle the underpass arrow so that the tip of the arrow stays on this side, we can figure out if it is left-handed or right-handed. We try to make the arrows point in the same direction. If you have to wiggle the underpass arrow clockwise to make them match, then it is a right-handed crossing. Likewise, if you have to wiggle the underpass arrow to counterclockwise to make them match, then it is a left-handed crossing.
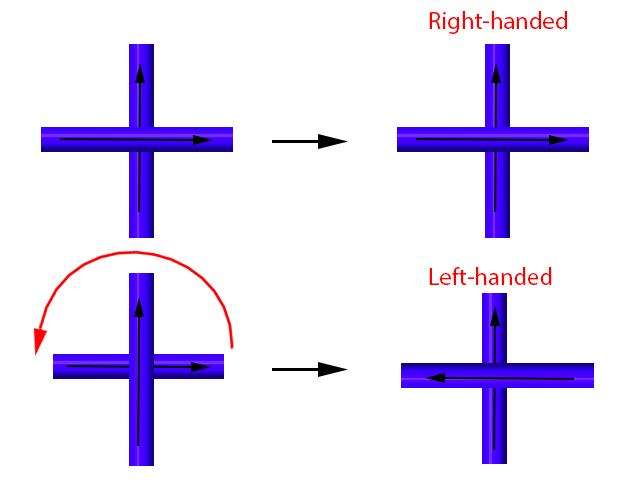
Another way to figure it out would be to keep the arrows fixed (so we don't wiggle them) and to rotate the knot diagram until the underpass arrow points upwards. If the overpass arrow points right, then it is right-handed. If the overpass arrow points left, then it is left-handed.
This is an interesting question and one worth thinking about. Let's think about standing on our knot diagram at a crossing, and choosing a direction to take. Regardless of what direction we choose, overpasses will remain overpasses, and underpasses will remain underpasses. Say we stand on the overpass and decide to head East. Say this path around the knot eventually comes back to our crossing, where it heads North. What kind of crossing is this?
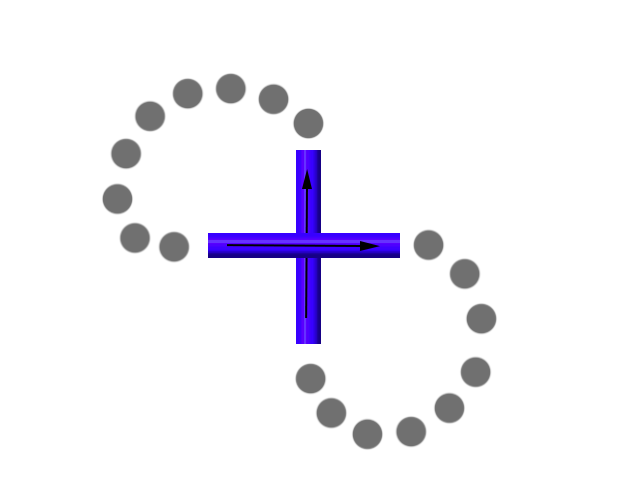
This is a right-handed crossing. If we think about how we treat the knot like one long path (grey), we know we have to come to our crossing twice. If we choose to go East the first time, then when we come back we are facing North. What about if we decide to go West first? Can we still come back facing North? It turns out that we cannot, since we would have to travel along a non-existent path (red).
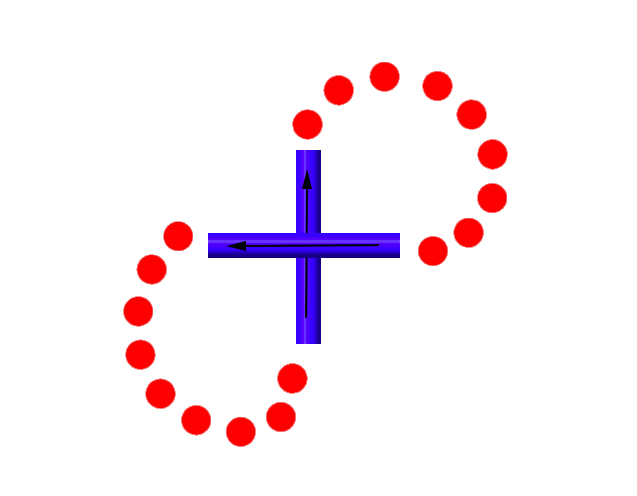
So if we go West instead, we are forced to come back going South. What kind of crossing is this? It turns out it's still a right-handed crossing.
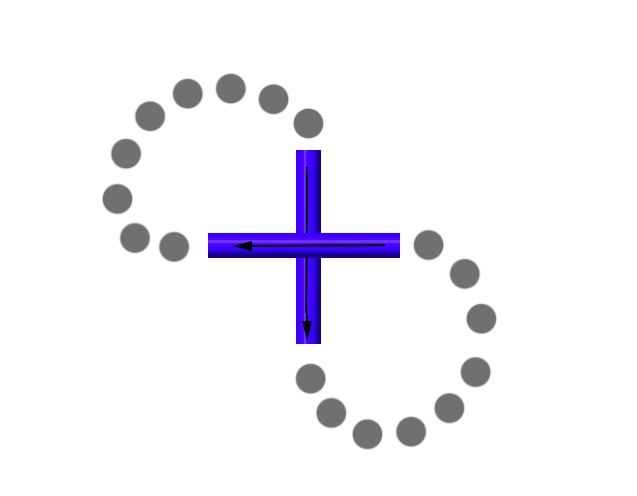
So have we really shown that handedness is independent of your choice of direction to traverse the knot diagram? Well, we never talked about any knot in particular - just some knot in general. We used the mathematical tool of abstraction to show that something is true regardless of specific details.
Sometimes knot theorists refer to right-handed crossings as positive crossings, and left-handed crossings as negative crossings. If we assign to each right-handed crossing the number $+1$ and to each left-handed crossing the number $-1$, we can compute a number called the writhe of a knot diagram. We simply add together all of the $+1$ and $-1$ at each crossing in the knot diagram.
Consider, for example, the following knot diagrams. We need to choose a direction to walk along the knots to be able to determine the handedness of each crossing. This in turn will let us number each crossing, which we can use to compute the writhe of each diagram.
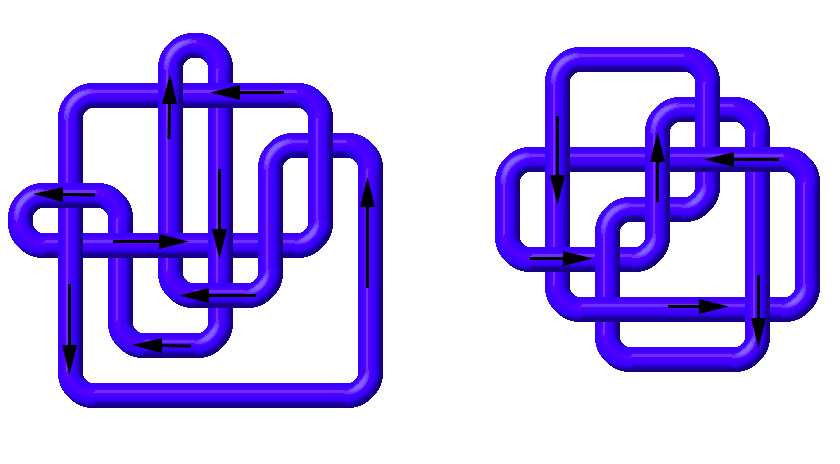
If we label each crossing with $+1$ or $-1$ based on its handedness, then we can compute the overall writhe of each diagram.
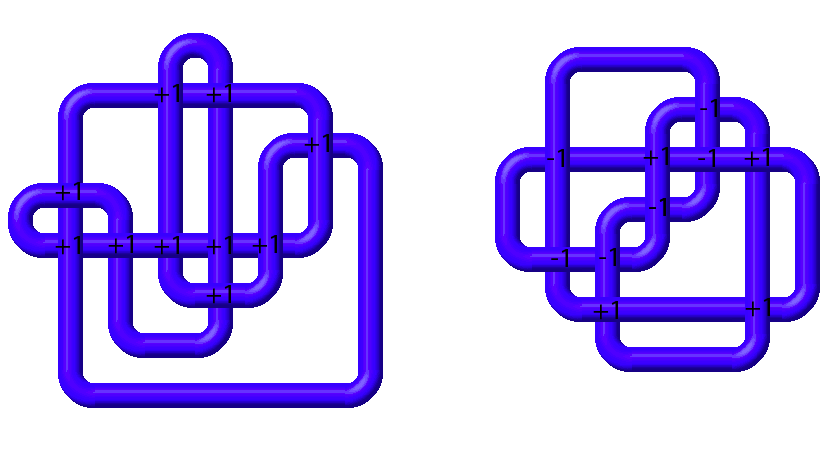
The diagram on the left has a writhe of $10$ since every crossing is right-handed (positive) and the knot has $10$ crossings. The diagram on the right has a writhe of $-2$ since there are $4$ right-handed (positive) crossings and $6$ left-handed (negative) crossings.
Strands are special sections of knot diagrams. There are two equivalent definitions of strands, but here we will choose just one. A strand is a section of the knot diagram, beginning at and underpass and ending at an underpass. Use the interactive canvas below to experiment with colouring in strands. Use Tools > Colour Knot to view the coloured knot.
We have discussed crossings, overpasses, underpasses and handedness of crossings. One question we might want to ask is: given a knot, is there a knot diagram for this knot with a minimum number of crossings? It turns out that the answer to this question is yes. The minimum number of crossings we can have in a knot diagram for a given knot is called the crossing number of a knot.
When mathematicians became interested in classifying, categorizing and tabulating (making a complete table of) knots, the crossing number was a natural way to organize knots. As the crossing number increases, knots become more complex to draw and harder to differentiate from one another - it turns out that finding the crossing number of a knot is not an easy task.
It turns out that there is only one knot with zero, one, and two crossings: the unknot. In fact, there are only fifteen distinct knots of fewer than 8 crossings.
A few of the knots we know of have names, like the unknot. Other knots, pictured at the beginning of this module, have names like the figure eight knot and the trefoil knot. However, there are infinitely many knots we can come up with. Does each get a special name? Mathematicians like being systematic and consistent, and during the history of knot tabulation, the Alexander-Briggs-Rolfsen notation was introduced based on the crossing numbers of knots. The notation is simply a number, corresponding to the crossing number of that knot, followed by a subscripted number that functions as an index for that knot. It's pretty much meaningless, except to allow mathematicians to be consistent when discussing knots, and to have a short name for each knot.
Use the interactive module below to look at the first few knots up to 8 crossings. Click "load" and choose a knot.
Despite the fact that this may look very different from the knot $4_1$ that can be loaded above, it is in fact this knot (the figure eight knot). One clue as to why these are the same knots lies in the number of crossings in the knot diagram. Both have $4$ crossings. We will prove in a later section that these are the same knot.
Unfortunately for us, we don't get to work with the 3D knots we are interested in very often. Since we can encode all of the information about a 3D knot in its 2D knot diagram, we instead work with the 2D knotS diagram. How can we tell that two knots are the same using their knot diagrams? We have to think about the kinds of transformations we can make to the knot diagram that don't change the knot that it represents.
Thankfully, a German mathematician named Kurt Reidemeister found that, given two knot diagrams that represent the same knot, one can be deformed into the other using a sequence of only three deformations of the knot diagram. Each move, called a Reidemeister move , is numbered based on the number of strands from the knot diagram that are involved when deforming it.
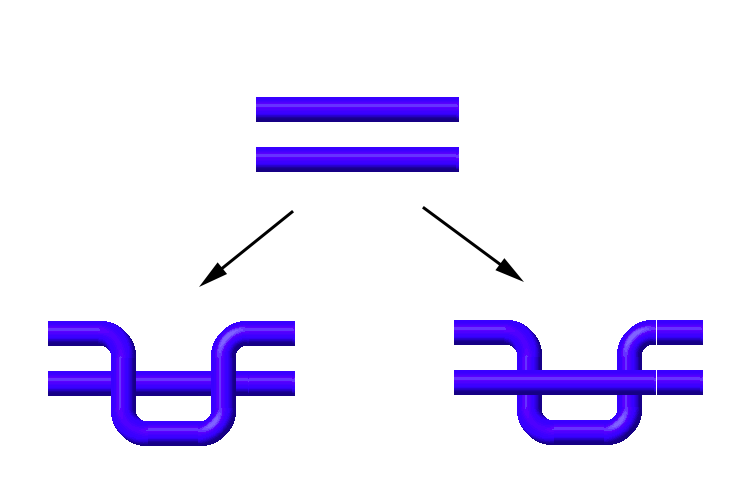
Type I Reidemeister moves either add or remove a twist from a knot diagram. When we add a twist, we are introducing a new right-handed or left-handed crossing.
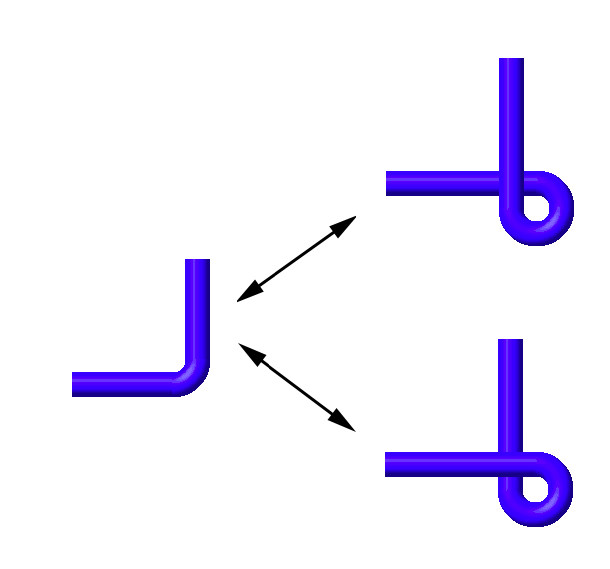
If we add a new right-handed crossing, the writhe increases by 1. If we add a new left-handed crossings, the writhe decreases by 1. If we remove a right-handed crossing, the writhe decreases by 1. If we remove a left-handed crossing, the writhe increases by 1.
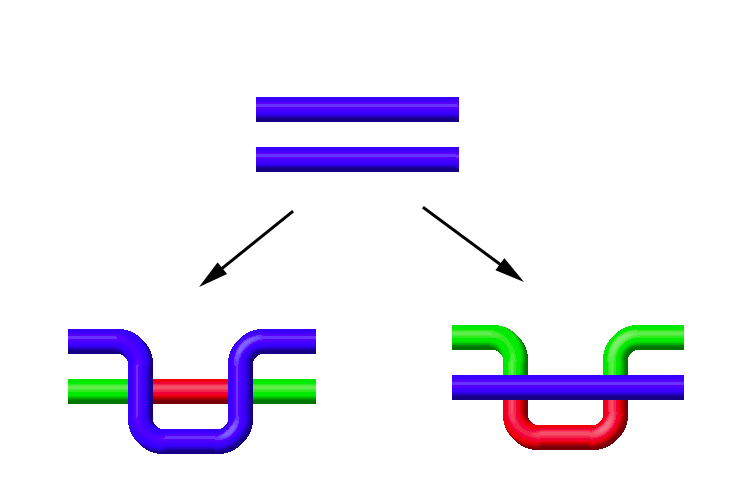
Type II Reidemeister moves pull one strand over another in a knot diagram.
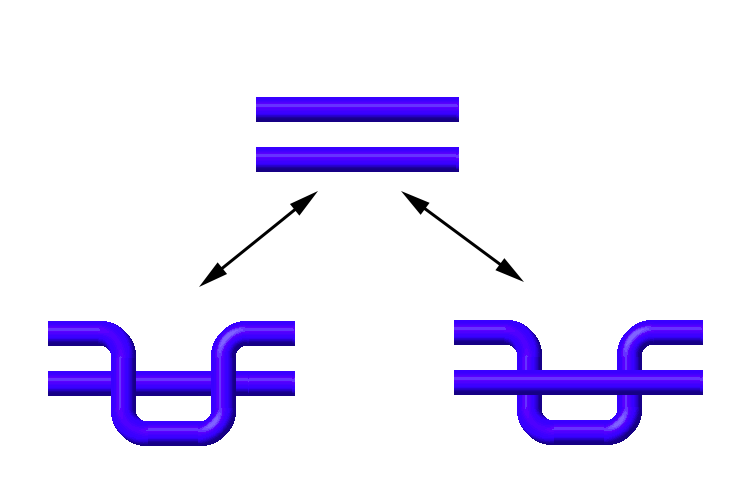
If we pull one strand over or under another, we are either adding two new crossings or removing two new crossings. The two crossings must have opposite handedness, so either we are adding a $+1$ and a $-1$, leaving the writhe unchanged, or we are removing a $+1$ and a $-1$, again leaving the writhe unchanged.
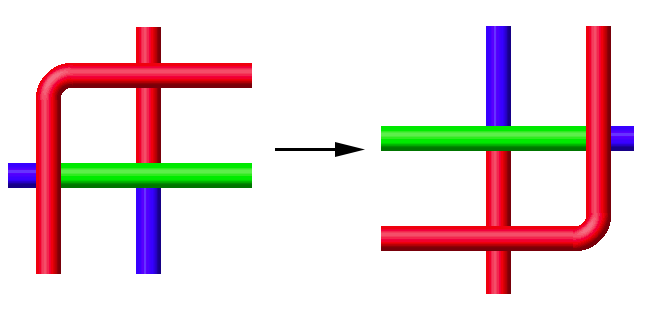
Type III Reidemeister moves pull one strand over a crossing. For performing a Reidemeister III move there must be a region surrounded by 3 strands that cross each other. One (top) strand crosses 2 times above, one (bottom) strand crosses 2 times below and one (middle) strand crosses once above and once below.
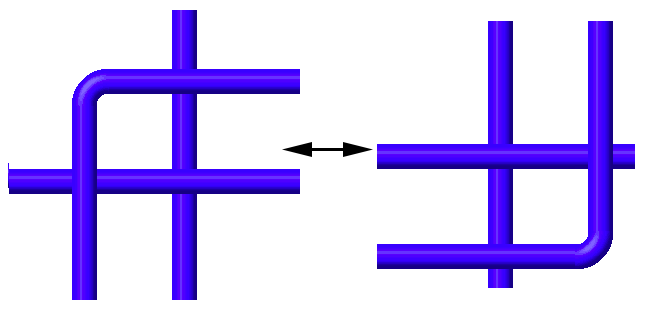
There are two symmetric cases where three strands cross three times, but they are in a sense 'stuck' since a type III move is not possible.
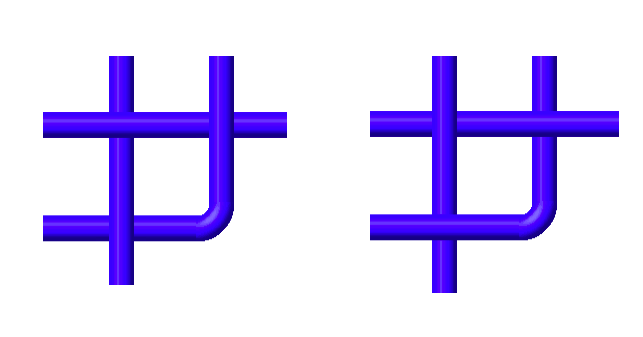
A knot invariant is a property of a knot that is unchanged regardless of the knot diagram you choose for this knot. Recall that we can go between knot diagrams for a given knot by only using Reidemeister moves. If we think we have a knot invariant, then, all we have to do is show that it is unchanged by Reidemeister moves. We have actually already encountered a knot invariant: the crossing number.
Mathematicians have discovered many knot invariants through different techniques and many have been rediscovered several times. In fact, there are methods of generating infinite families of knot invariants.
Sadly for us, we cannot always use knot invariants to uniquely identify a knot. However, if two different knots have different values for a knot invariant, we can tell that they are for sure different knots.
- At least two colours must be used.
- At each crossing, either all three strands (two from underneath, one overtop) must be all different colours, or all the same colour.
We say that a knot is tricolourable when it meets the above criteria. Try to figure if any of the knots up to 8 crossings are tricolourable by loading them and using the 'Colour Knot' option. Remember to follow all the rules of tricolourability!
Recall that to show something is a knot invariant, we must show that it does not change when applying any of the three Reidemeister moves. Let's assume that a knot diagram is tricolourable.
When applying a Type I Reidemeister move, we can easy maintain tricolourability by colouring the newly introduced strands the same colour.
When applying a Type II Reidemeister move on two differently coloured strands, we can colour the newly introduced strand that we form a third colour.
When applying a Type III Reidemeister move, we can also show tricolourability is preserved.
If both initial strands are the same colour, then we can colour the newly formed strand the same colour as well to preserve tricolourability.
The unknot is not tricolourable (since it cannot be coloured with more than two colours). Since tricolourability is a knot invariant, no projection or knot diagram of the unknot is tricolourable (try this for yourself!). If we have a knot diagram that is tricolourable, then it must necessarily not be the unknot.
If we allowed just one colour to be used, then every knot would be tricolourable and the property would be trivial (it would not be helpful or special). If we allow two colours to be used, we find that no amount of reidemeister moves let us colour the unknot with 2 colours while following the other rule regarding colours of incident strands at crossings.
Try to tricolour the following knot.
Did you find a solution? Here is a picture showing we cannot tricolour the knot.

You should never take what you read for granted. Try other tricolourations! Maybe mathematicians got this one wrong.
We know that there are more knots than just the unknot, and that they are distinct from each other. One question we can ask is how different a knot is from the unknot. One way we can answer this question is by asking how many times we would have to pass the knot through itself to be able to untangle it into the unknot. If we think about this in terms of our knot diagrams, the question becomes: how many crossings do we have to switch (overpass to underpass or underpass to overpass) so that we can deform the diagram into the unknot? This number is called the unknotting number of a knot.
For example, the unknotting number of the $4_1$ knot is 1. We can switch a single crossing and deform it into the unknot.

After switching the crossing (U), we get the second knot diagram. We can do a type I to undo the loop to the right. We can then do a type II to pull that strand under the vertical strand on the right. We can then do another type I to undo the last cross, and squish it back to a circle (the unknot).

Try to experiment with the following module by switching a crossing (double click) and clicking 'minimize'. How many times do you have to switch a crossing before it becomes completely unknotted?
When you're done, press 'reset' and see what the smallest number you can find is. This is the unknotting number. What can you say about the unknotting number of these knots? If they are different, what can we say about the knots? What about if they are the same?
First we should clarify what we mean by "simplify the diagram". In this case, if reversing a crossing simplifies the diagram, then it should be in some case closer to the unknot. What this means is that reversing a crossing should produce a new knot diagram with a lower unknotting number.
Second, we should realize that when we are talking about these knot diagrams, we can introduce a crossing by doing a Reidemeister I move. That crossing will obviously not help simplify the knot if we reverse it. So when we are talking about unknotting numbers, we are interested in reversing crossings on knot diagrams that reduce the crossing number of the knot.
The module below shows the knot diagram for the knot $8_1$. What is the minimum number of crossings that must be switched to produce the unknot?
If we can switch one crossing to go from the knot $8_1$ to the unknot, then we can obviously go from the unknot to the knot $8_1$ by switching one crossing. This knot belongs to a family of knots called twist knots. You can imagine making them by taking the unknot and stretching it out into a long, thin oval. Then twist each end in opposite directions so that it begins to twist in the middle. Then, take the two ends of the loop you made and pass one end through the other to make a knot.
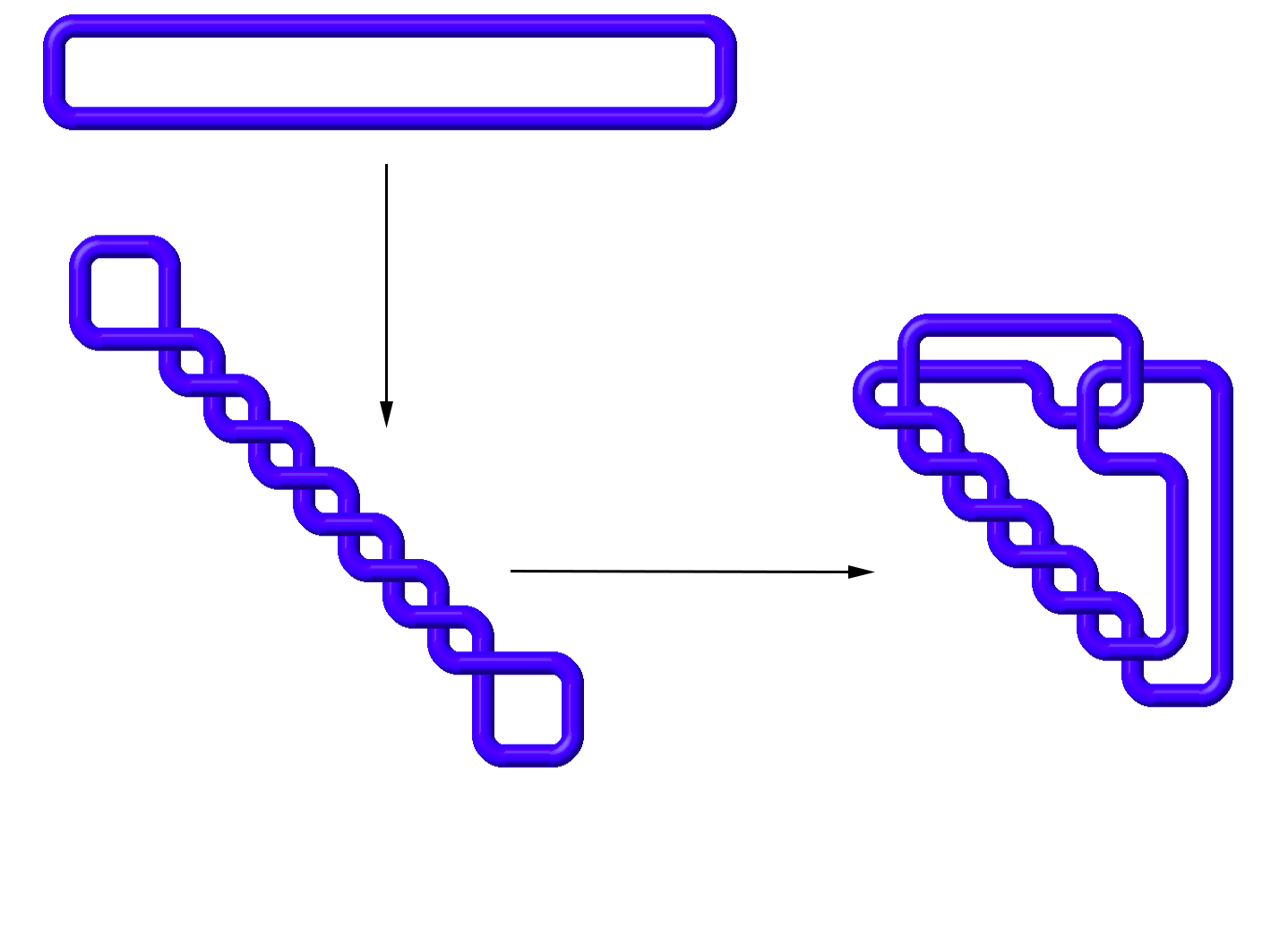
While there are infinitely many knot diagrams for a given knot, many of those knot diagrams are only slightly different visually. They might be rotations of the same diagram, or be slightly stretched out more in one direction than another.
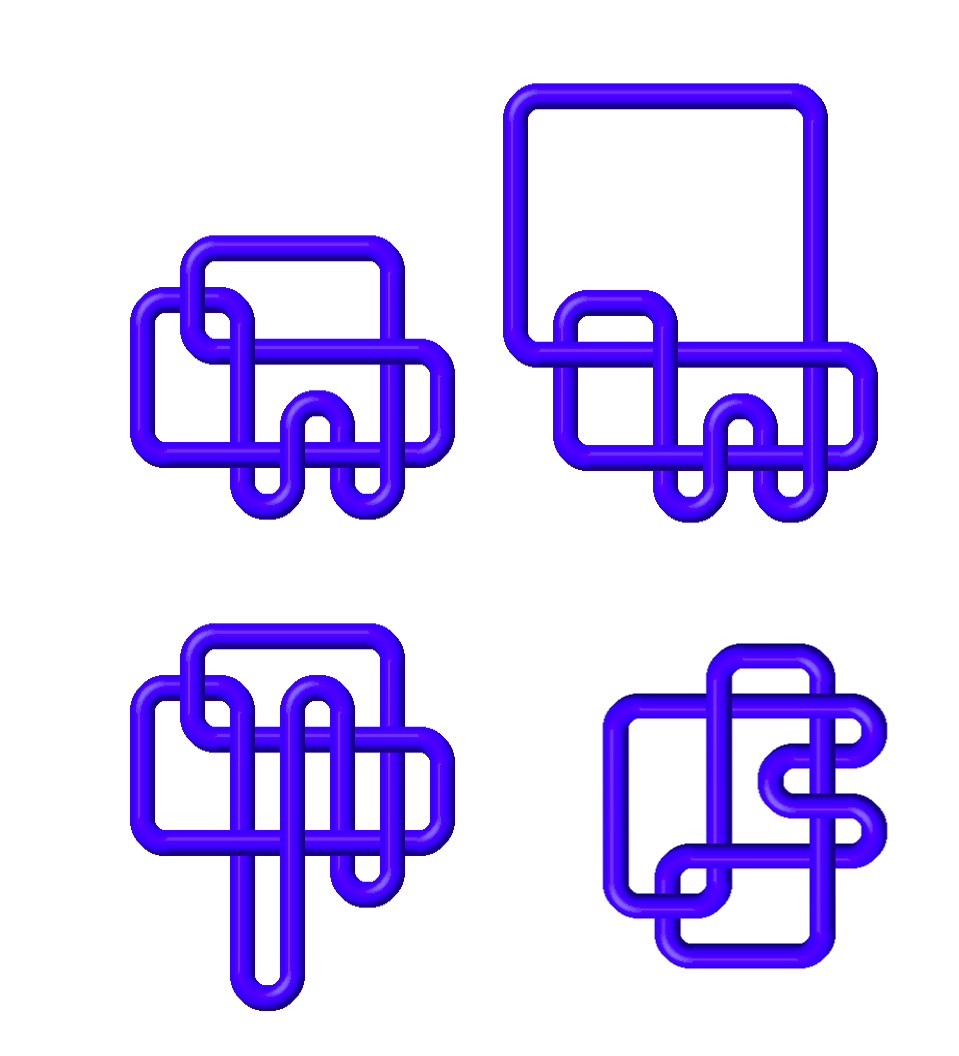
Nothing important has changed between these diagrams. What information from a knot diagram, then, is important to us? How can we encode the knot diagram so that someone else can reconstruct it without looking at it?
Dowker-Thistlewaite (DT) notation is a way of encoding the knot diagram that is focused on the crossings of the diagram
Imagine standing anywhere on the knot diagram that is not a crossing. Pick a point on the knot diagram and begin walking along it until you reach a crossing. Label this crossing with a $1$. If you are walking along an overpass label the crossing with a $+$, and if you are walking along an underpass label the crossing with a $-$. Continue along the knot line until you get to the next crossing. Label it with a $2$. At each new crossing, label that crossing with a new number that is one greater than the previous crossing's label. If the number being assigned is an odd number, assign the crossing a $+$ if you are walking along an overpass and a $-$ if you are walking along an underpass. At the end, every crossing will have two labels: an even number, an odd number, and a sign.
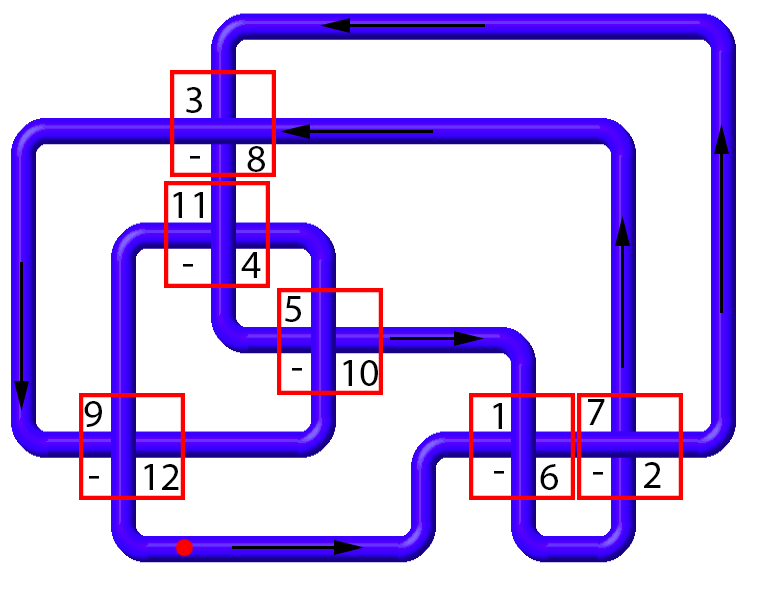
Each crossing has two numbers associated with it. If we begin at the crossing labelled 1 and write down the sign and the even number at this crossing, we get the first entry in the DT code. If we continue on to the next odd number crossing (3) and do the same thing, we get the next entry. By going to each odd-numbered crossing in order, beginning at 1, we can get the DT code for the entire knot.
Let us begin by traversing each odd-numbered crossing in order, writing down the associated even-numbered crossing and sign. $$ \begin{matrix} 1 & 3 & 5 & 7 & 9 & 11 \\ 6 & 8 & 10 & 2 & 12 & 4 \\ - & - & - & - & - & - \end{matrix} $$ This leaves us with a final Dowker code of $$ -6 \ -8 \ -10 \ -2 \ -12 \ -4 $$
If you traverse the knot in the opposite direction starting from the same point, the signs assigned to each crossing in the Dowker-Thistlewaite (DT) notation will reverse. This happens because the direction of traversal determines whether a crossing is labeled as an overpass or an underpass.
In the original direction, if you encounter a crossing where the strand you are on passes over another strand, it is assigned a "+" sign, and if it passes under, it is assigned a "-" sign. When the direction is reversed, the roles of overpass and underpass are swapped for each crossing. What was previously an overpass is now an underpass, and vice versa. As a result, the "+" signs in the original traversal will become "-" signs, and the "-" signs will become "+" signs.
Thus, the signs in the DT notation are entirely inverted when the traversal direction is reversed, but the sequence of even numbers associated with each odd crossing remains unchanged. This reflects the symmetry and reversibility inherent in the knot diagram.


