Historia

Arquímedes de Siracusa

Arquímedes fue un matemático, físico, ingeniero, inventor y astrónomo griego. Nació en el año 287 a. C. en Siracusa, Sicilia. A pesar de que se conocen pocos detalles de su vida, Arquímedes es generalmente considerado como el más grande matemático de la antigüedad y uno de los más grandes de todos los tiempos. Inventó una bomba para elevar el agua de un río y un "espejo ardiente" parabólico, que se utilizaban para concentrar los rayos del sol en los barcos de madera, incendiándolos.

Quizás una de las historias más famosas sobre él es la de su descubrimiento del principio de flotabilidad. La flotabilidad es una fuerza ascendente ejercida por un fluido (como el agua) que trabaja para mantener los objetos a flote o ralentizar su descenso en el fluido. La historia dice que Arquímedes descubrió el principio de flotabilidad mientras se bañaba y se emocionó tanto que corrió desnudo a la calle gritando "¡Eureka!".

A Arquímedes también se le atribuye el desarrollo de algunas de las ideas del cálculo, casi 2000 años antes de su creación por Sir Isaac Newton y Gottfried Leibniz; También es reconocido por su notable y precisa aproximación de pi (π).

En su obra "El contador de arena", Arquímedes se propuso la tarea imposible de calcular el número de granos de arena que podía contener el universo. Desafió que no era imposible hacerlo, incluso si los granos de arena eran demasiado pequeños o demasiados para ser contados. Para resolver el problema de los granos de arena, Arquímedes inventó un sistema basado en la miríada o "incontable" en griego (también se denota 10.000 en el sistema numérico griego). Fijó un sistema numérico utilizando potencias de una miríada de miríadas (10.000 x 10.000 = 100 millones) y finalmente calculó el número de granos de arena en el universo como 8 x^10.63 granos. Arquímedes murió en el año 212 a.C. en Siracusa.

Fuentes:

Musser, Gary. Hamburguesa, Guillermo. Peterson, Blake. Matemáticas para profesores de primaria: un enfoque contemporáneo, 6ª ed.; Wiley.

Burton, D.M. La historia de las matemáticas: una introducción, 5ª ed.; McGraw-Hill: Nueva York, 2003.

http://www.ancientgreece.com/s/People/Archimedes/

http://en.wikipedia.org/wiki/Archimedes>

Aristóteles

Aristóteles fue un filósofo griego que nació en el 384 a.C. y murió en el 322 a.C. Estudió casi todas las materias posibles en ese momento, así como contribuyó a la mayoría de ellas. Es bien sabido que fue la última persona en saber todo lo que había que saber, al menos lo que se sabía en ese momento. La contribución de Aristóteles a las matemáticas se encuentra en el campo de la lógica. Por ejemplo, el hecho de que "todos los humanos son mortales" y "todos los griegos son humanos" le permitió concluir que "todos los griegos son mortales", descubriendo así lo que ahora se llaman reglas de validez. También abrió una escuela llamada el Liceo. Impartió varios cursos allí durante doce años después de su inauguración. Gran parte de su obra se ha perdido.

Fuentes:

http://www.edu.pe.ca/kish/Grassroots/math/aristotl.htm

http://en.wikipedia.org/wiki/Aristotle

Thomas Bayes

Thomas Bayes, nacido en 1701, fue un matemático inglés y ministro presbiteriano. Formuló un teorema llamado teorema de Bayes sobre la probabilidad inversa. A menudo uno piensa en que le den cuántas canicas rojas y azules hay en una caja y le pidan que calcule la probabilidad de elegir una canica azul, mientras que a Bayes le interesaba que le dieran la probabilidad de elegir una canica azul o roja de una caja y tener que calcular cuántas canicas rojas y azules había en la caja. Curiosa y desafortunadamente, su logro más famoso radicó en sus notas preliminares, que fueron editadas y publicadas por Richard Price poco después de la muerte de Bayes.

Fuentes:

http://bayesian.org/bayes

http://en.wikipedia.org/wiki/Thomas_Bayes

Brahmagupta

Brahmagupta fue uno de los más grandes matemáticos y astrónomos indios del siglo VII. Era del estado de Rajastán, en el noroeste de la India. Uno de los temas que consideró son las soluciones de números enteros de lo que hoy se llaman ecuaciones de Pell como x² − 92y² = 1, y dijo: "[una persona que resuelva este problema] dentro de un año [es] un matemático".

Brahmagupta explicó cómo encontrar el cubo y la raíz cúbica de un número entero y encontró fórmulas explícitas para la suma de los cuadrados de los primeros n números naturales y la suma de los cubos de los primeros n números naturales. Su mayor contribución, sin embargo, fue su tratamiento del (entonces relativamente nuevo) número cero. Se le ocurrieron reglas para sumar, restar y multiplicar números por cero. Su "Brahmasphutasiddhanta" es el texto más antiguo conocido que reconoce el cero como un número en lugar de solo un dígito de marcador de posición o un símbolo que representa una falta de cantidad.

Fuentes:

https://www.storyofmathematics.com/indian_brahmagupta.html

Chen Jingrun

Chen Jingrun (22 de mayo de 1933 - 19 de marzo de 1996) fue un matemático chino que realizó importantes contribuciones a la teoría de números. Su trabajo sobre la conjetura de los primos gemelos, el problema de Waring, la conjetura de Goldbach y la conjetura de Legendre condujo al progreso de la teoría analítica de números. En un artículo de 1966 demostró lo que ahora se llama el teorema de Chen: todo número par suficientemente grande puede escribirse como la suma de un número primo y un semiprimo (el producto de dos números primos), por ejemplo, 100 = 23 + 7,11.

Fuentes:

https://en.wikipedia.org/wiki/Chen_Jingrun

John Horton Conway

John Horton Conway (26 de diciembre de 1937 - 11 de abril de 2020) fue un matemático inglés activo en la teoría de grupos finitos, la teoría de nudos, la teoría de números, la teoría de juegos combinatorios y la teoría de codificación. Muchos de los juegos interactivos de Caribou han sido influenciados por su investigación, incluyendo juegos combinatorios como Hackenbush o Chomp, Sliding Blocks, y un juego de nudos actualmente en desarrollo.

Conway también hizo contribuciones a muchas ramas de las matemáticas recreativas, sobre todo la invención de un autómata celular bidimensional llamado el Juego de la Vida, ayudando a lanzar un campo completamente nuevo de las matemáticas con aplicaciones en ciencias de la computación, física y biología teórica. En los autómatas celulares, se estudia el comportamiento de una red finita de células en la que cada célula tiene un estado entre un número finito de estados en cada punto en el tiempo, y donde el estado de cada célula cambia a medida que avanza el tiempo de acuerdo con un conjunto de reglas, normalmente una función matemática. También es conocido por el descubrimiento de los números surrealistas.

Nacido y criado en Liverpool, a los 11 años Conway aspiraba a convertirse en matemático. Pasó la primera mitad de su carrera en la Universidad de Cambridge antes de trasladarse al estado estadounidense de Nueva Jersey, donde ostentó el título de profesor emérito John von Neumann en la Universidad de Princeton durante el resto de su carrera, retirándose en 2013. El 11 de abril de 2020, a los 82 años, falleció por complicaciones de la COVID-19.

Fuentes:

https://en.wikipedia.org/wiki/John_Horton_Conway

https://en.wikipedia.org/wiki/Cellular_automaton

René Descartes

René Descartes fue un filósofo y matemático francés, nacido el 31 de marzo de 1596 en Touraine, Francia. Descartes ha sido acreditado como el "Padre de la Filosofía Moderna" y el "Padre de la Geometría Analítica", que es la rama entre el álgebra y la geometría. Antes de la época de Descartes, los temas de álgebra y geometría se habían desarrollado en vías paralelas, hasta que desarrolló un método para unirlas. Esta importante contribución permitió a Descartes, junto con Newton y Leibniz, proporcionar los fundamentos del cálculo moderno. El sistema de coordenadas utilizado hoy en día en la geometría analítica se llama sistema de coordenadas cartesiano en su honor.

La geometría analítica de Descartes fue diseñada para estudiar los atributos matemáticos de las líneas y curvas representándolos a través de ecuaciones. Una de las contribuciones más importantes de Descartes fueron sus escritos filosóficos. Descartes, que estaba convencido de que la ciencia y las matemáticas podían utilizarse para explicar todo en la naturaleza, fue el primero en describir el universo físico en términos de movimiento y materia, viendo el universo como una máquina gigante diseñada matemáticamente.

René Descartes escribió tres textos importantes: (1) Discurso del método para conducir correctamente la razón y buscar la verdad en las ciencias, (2) Meditaciones sobre la filosofía primera y (3) Principios de filosofía.

Descartes siempre había sido un individuo frágil, a menudo pasaba la mayor parte de sus mañanas en la cama, donde pensaba la mayor parte de sus pensamientos, recién salido de sueños en los que a menudo tenía sus revelaciones. En sus últimos años, Descartes tuvo que trasladarse a Suecia para dar clases particulares de filosofía a la reina Cristina. Desafortunadamente, la Reina era una madrugadora que quería sus lecciones a las 5:00 de la mañana. Este horario no ayudó a la frágil salud de Descartes. Contrajo una neumonía, de la que murió el 11 de febrero de 1650 a la edad de 54 años.

La famosa preposición de Descartes: Cogito ergo sum - "Pienso, luego existo".

Fuentes:

Burton, D.M. La historia de las matemáticas: una introducción, 5ª ed.; McGraw-Hill: Nueva York, 2003.

http://plato.stanford.edu/entries/descartes/

http://www.iep.utm.edu/descarte/

Musser, Gary. Hamburguesa, Guillermo. Peterson, Blake. Matemáticas para profesores de primaria: un enfoque contemporáneo, 6ª ed.; Wiley.

https://en.wikipedia.org/wiki/Ren%C3%A9_Descartes

Euclides de Alejandría

Euclides fue un matemático griego, a menudo referido como el "Padre de la Geometría", nacido alrededor del año 325 a. C. Poco se sabe sobre la vida de Euclides, ya que solo hay un puñado de referencias a él. La fecha y el lugar del nacimiento de Euclides y la fecha y las circunstancias de su muerte se desconocen y sólo se estiman aproximadamente en proximidad con las figuras contemporáneas mencionadas en las referencias. Las pocas referencias históricas a Euclides fueron escritas siglos después de su vida, por Proclo y Pappus de Alejandría. Se sabe muy poco de la vida de Euclides, excepto que enseñó en Alejandría. En su libro Elementos, Euclides dedujo los principios de lo que ahora se llama geometría euclidiana. Euclides murió en el año 265 a.C. en Alejandría, Egipto.

Fuentes:

Musser, Gary. Hamburguesa, Guillermo. Peterson, Blake. Matemáticas para profesores de primaria: un enfoque contemporáneo, 6ª ed.; Wiley.

Burton, D.M. La historia de las matemáticas: una introducción, 5ª ed.; McGraw-Hill: Nueva York, 2003.

http://www.businessinsider.com/important-mathematicians-modern-world-2012-7?op=1

https://en.wikipedia.org/wiki/Euclid

Leonhard Euler

Leonard Euler fue un matemático y físico suizo pionero, nacido el 15 de abril de 1707 en Basilea, Suiza. Hizo notables contribuciones a los campos del cálculo infinitesimal y la teoría de grafos. Euler también introdujo gran parte de la terminología y notación matemática moderna, particularmente para el análisis matemático, como la noción de funciones matemáticas. Por ejemplo, el uso moderno del símbolo π se debe a Euler.

En geometría, es mejor conocido por la línea de Euler de un triángulo y la fórmula F + V = E + 2. En esta fórmula, Euler relaciona el número de caras (F), vértices (V) y aristas (E) de un poliedro en un espacio tridimensional.

Al principio de su carrera, Euler perdió la vista en su ojo derecho, probablemente debido al exceso de trabajo. Publicó más de 500 libros y artículos a lo largo de su vida, y se ha calculado que sus publicaciones durante su vida laboral tuvieron una media de 800 páginas al año. A partir de 1771 quedó totalmente ciego, pero sus descubrimientos matemáticos continuaron. Trabajaba mentalmente y luego dictaba a los asistentes, a menudo usando una gran pizarra en la que escribía las fórmulas para ellos.

Euler también derivó la base del logaritmo natural con e, también conocido como número de Euler, como una constante matemática aproximadamente igual a 2.71828. e es el límite de (1 + 1/n)ⁿ cuando n se aproxima a infinito.

Euler murió en 1783 a la edad de 76 años, permaneciendo activo hasta el final.

Fuentes:

Musser, Gary. Hamburguesa, Guillermo. Peterson, Blake. Matemáticas para profesores de primaria: un enfoque contemporáneo, 6ª ed.; Wiley.

Leonard Euler fue un matemático y físico suizo pionero, nacido el 15 de abril de 1707 en Basilea, Suiza. Hizo notables contribuciones a los campos del cálculo infinitesimal y la teoría de grafos. Euler también introdujo gran parte de la terminología y notación matemática moderna, particularmente para el análisis matemático, como la noción de funciones matemáticas. Por ejemplo, el uso moderno del símbolo π se debe a Euler.

En geometría, es mejor conocido por la línea de Euler de un triángulo y la fórmula F + V = E + 2. En esta fórmula, Euler relaciona el número de caras (F), vértices (V) y aristas (E) de un poliedro en un espacio tridimensional.

Al principio de su carrera, Euler perdió la vista en su ojo derecho, probablemente debido al exceso de trabajo. Publicó más de 500 libros y artículos a lo largo de su vida, y se ha calculado que sus publicaciones durante su vida laboral tuvieron una media de 800 páginas al año. A partir de 1771 quedó totalmente ciego, pero sus descubrimientos matemáticos continuaron. Trabajaba mentalmente y luego dictaba a los asistentes, a menudo usando una gran pizarra en la que escribía las fórmulas para ellos.

Euler también derivó la base del logaritmo natural con e, también conocido como número de Euler, como una constante matemática aproximadamente igual a 2.71828. e es el límite de (1 + 1/n)ⁿ cuando n se aproxima a infinito.

Euler murió en 1783 a la edad de 76 años, permaneciendo activo hasta el final.

Fuentes:

Musser, Gary. Hamburguesa, Guillermo. Peterson, Blake. Matemáticas para profesores de primaria: un enfoque contemporáneo, 6ª ed.; Wiley.

http://www.businessinsider.com/important-mathematicians-modern-world-2012-7?op=1

Pierre de Fermat

Pierre de Fermat, nacido el 17 de agosto de 1607, fue un abogado francés y un matemático aficionado que contribuyó con trabajos que finalmente condujeron al cálculo infinitesimal, incluida su técnica de adcualidad. Fermat y René Descartes fueron los dos principales matemáticos de principios del siglo XVII. Es mejor conocido por el último teorema de Fermat, que dice que "no hay tres enteros positivos a, b y c que puedan satisfacer la ecuación aⁿ + bⁿ = cⁿ para cualquier valor entero de n mayor que dos".

Fermat escribió su último teorema en el margen de un libro. Afirmó que no tenía espacio para escribir una demostración del teorema. La prueba no se pudo encontrar durante más de 350 años, ya que otros matemáticos no pudieron deducirla. Andrew Wiles lo intentó y no lo consiguió, pero más tarde lo consiguió junto a Richard Taylor.

Fuentes:

Musser, Gary. Hamburguesa, Guillermo. Peterson, Blake. Matemáticas para profesores de primaria: un enfoque contemporáneo, 6ª ed.; Wiley.

http://en.wikipedia.org/wiki/Pierre_de_Fermat

José Fourier

Joseph Fourier, nacido el 21 de marzo de 1768, fue un matemático y físico francés. Quedó huérfano a la edad de nueve años y aceptó una cátedra militar de matemáticas después de ser educado, contribuyendo con muchos trabajos de matemáticas al Instituto Egipcio. Napoleón Bonaparte nombró a Fourier prefecto (gobernador) del departamento de Isère en Grenoble, donde supervisó los proyectos de construcción después de retomar su puesto académico como profesor en la école Polytechnique. Es mejor conocido por descubrir las series de Fourier y sus aplicaciones a varios problemas en los temas de transferencia de calor y vibraciones. La transformada de Fourier y la Ley de Fourier también llevan su nombre en su honor. También se le atribuye el descubrimiento del efecto invernadero.

Fuentes:

http://scienceworld.wolfram.com/biography/Fourier.html

http://en.wikipedia.org/wiki/Joseph_Fourier

Galileo Galilei

Galileo Galilei nació el 15 de febrero de 1564 en Pisa, Italia. Es conocido por ser el primer científico moderno. Su padre quería que estudiara medicina, por lo que Galileo se matriculó en la Universidad de Pisa para hacerlo, pero abandonó los estudios poco después para dedicarse a su pasión, las matemáticas y la mecánica. Entre sus muchas contribuciones a las matemáticas, ideó y mejoró una brújula geométrica y militar. También entendía muy bien la parábola. A Galileo le ofrecieron una cátedra de matemáticas en la Universidad de Padua, que aceptó con gratitud y trabajó como catedrático durante dieciocho años.

Galileo fue considerado sospechoso de herejía, ya que creía que el Sol permanece inmóvil en el centro del universo, mientras que la Tierra no permanece inmóvil ni está en el centro del universo. Esta creencia contrastaba con las Sagradas Escrituras. Fue condenado a prisión formal, y luego se le conmutó la pena por arresto domiciliario por el resto de su vida, sin que se le permitiera publicar ninguna de sus obras a partir de entonces. Murió el 8 de enero de 1642, tras sufrir fiebre, palpitaciones y otros malestares. Deseaba ser enterrado junto a su padre, pero la Iglesia le denegó este deseo debido al delito del que se le acusaba.

Fuentes:

http://math.berkeley.edu/~robin/Galileo/life.html

http://en.wikipedia.org/wiki/Galileo_Galilei

Carl Friedrich Gauss

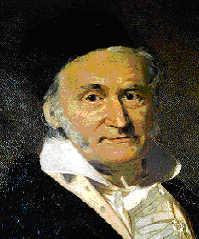
Carl Gauss fue un matemático y físico alemán nacido el 30 de abril de 1777 en Braunschweig, Sacro Imperio Romano Germánico. A menudo conocido como el Princeps mathematicorum (en latín, "El Príncipe de los Matemáticos"), Gauss tuvo una notable influencia en muchos campos de las matemáticas, incluyendo la teoría de números, el álgebra, la estadística, el análisis y la geometría diferencial. Se refirió a las matemáticas como "la reina de las ciencias".

Hay varias historias sobre Gauss a una edad muy temprana. Según uno de ellos, sus dones se hicieron evidentes cuando a la edad de tres años, mentalmente y sin fallar en sus cálculos, corrigió un error que su padre había cometido en el papel mientras calculaba las finanzas. Otra famosa historia cuenta que en la escuela primaria, después de que el joven Gauss se portara mal, su maestro, J.G. Büttner, le dio la tarea de agregar una lista de números enteros del 1 al 100, en progresión aritmética. Al parecer, el joven Gauss dio la respuesta correcta en cuestión de segundos, ante el asombro de su profesor y de su ayudante Martin Bartels. El método de Gauss se basaba en la adición por pares de términos de extremos opuestos de la lista, lo que daba sumas intermedias idénticas. Por ejemplo: 1 + 100 = 101, 2 + 99 = 101, 3 + 98 = 101, y así sucesivamente, para una suma total de 50 x 101 = 5050.

A la edad de 18 años, Gauss ideó un método para construir un polígono regular de 17 lados, usando solo una brújula y una regla. Sorprendentemente, luego derivó una regla general que predijo qué polígonos regulares son construibles de manera similar. En 1807 se convirtió en el director del observatorio astronómico de Göttingen, Alemania, donde sirvió hasta su muerte. Gauss murió el 25 de febrero de 1855.

Fuentes:

Musser, Gary. Hamburguesa, Guillermo. Peterson, Blake. Matemáticas para profesores de primaria: un enfoque contemporáneo, 6ª ed.; Wiley.

http://en.wikipedia.org/wiki/Carl_Friedrich_Gauss#Anecdotes

Kurt Gödel

Kurt Friedrich Gödel, nacido el 28 de abril de 1906, fue un lógico, matemático y filósofo austríaco. Considerado junto a Aristóteles y Frege como uno de los lógicos más importantes que se conocen, tuvo un impacto significativo en el pensamiento científico y filosófico del siglo XX al publicar sus dos teoremas de incompletitud cuando tenía solo 25 años, solo un año después de terminar su doctorado en la Universidad de Viena. Gödel desarrolló una técnica llamada numeración de Gödel para demostrar el primer teorema, que codifica expresiones formales como números naturales. También aclaró las relaciones entre la lógica clásica, intuicionista y modal.

Cuando Gödel envejeció, sufrió períodos de inestabilidad mental y enfermedad. Tenía una paranoia obsesiva de ser envenenado, lo que lo llevó a comer solo la comida que su esposa le servía. Cuando estuvo hospitalizado durante 6 meses y no pudo cuidarlo, Gödel se negó a comer y murió de hambre por eso.

Fuentes:

http://www-history.mcs.st-and.ac.uk/Biographies/Godel.html

http://en.wikipedia.org/wiki/Kurt_Godel

Hipatia de Alejandría

Hipatia de Alejandría, nacida en el año 350 d. C., fue la primera mujer que realizó una contribución sustancial al desarrollo de las matemáticas que aún se conocen. Hipatia era hija del matemático y filósofo Teón de Alejandría y es bastante seguro que estudió matemáticas bajo la guía e instrucción de su padre. En la universidad de Alejandría, fue una famosa profesora de matemáticas y filosofía, pero se desconoce si realmente ocupó un puesto docente. Hipatia llegó a simbolizar el conocimiento y la ciencia que los primeros cristianos identificaban con el paganismo. Sin embargo, entre los alumnos a los que enseñó en Alejandría había muchos cristianos prominentes. Uno de los más famosos es Sinesio de Cirene, que más tarde se convertiría en obispo de Tolemaida. Hipatia se convirtió en víctima de los prejuicios de su tiempo. Hubo brotes periódicos de violencia, y durante uno de estos incidentes Hipatia fue asesinada por una turba de fanáticos cristianos.

Fuentes:

http://www-history.mcs.st-and.ac.uk/Biographies/Hypatia.html

Musser, Gary. Hamburguesa, Guillermo. Peterson, Blake. Matemáticas para profesores de primaria: un enfoque contemporáneo, 6ª ed.; Wiley.

Katherine Johnson

Katherine Johnson fue una notable matemática nacida el 26 de agosto de 1918 en White Sulfur Springs, Virginia Occidental. Desde muy joven fue inteligente y curiosa. A la edad de 13 años, Johnson asistió a la escuela secundaria y luego se graduó con los más altos honores del State College a la edad de 18 años. En 1939, fue elegida por el presidente del estado para ser una de las tres primeras estudiantes negras en asistir a las escuelas de posgrado de la Universidad de Virginia Occidental. Estudió matemáticas, pero se fue poco después para formar una familia.

En 1952, Johnson se enteró de los puestos vacantes en la sección de Computación del Área Oeste en el laboratorio Langley del Comité Asesor Nacional de Aeronáutica (NACA). Apenas dos semanas después de asumir el cargo, fue asignada a un proyecto en la Rama de Cargas de Maniobra de la División de Investigación de Vuelo. Pasó los siguientes cuatro años analizando datos de pruebas de vuelo y trabajó en la investigación de un accidente aéreo causado por la turbulencia de la estela.

Johnson continuaría haciendo numerosas contribuciones significativas a las misiones espaciales. Hizo análisis de trayectoria para la misión Freedom 7 de Alan Shepard en mayo de 1961. En particular, realizó cálculos para la misión Apolo 11 de 1969, que envió a los tres primeros hombres a la Luna. Johnson fue autor o coautor de 26 informes y se retiró en 1986. En 2015, a los 97 años, el presidente Barack Obama le otorgó la Medalla Presidencial de la Libertad y en 2016, la NASA nombró un edificio en su honor. Katherine Johnson murió el 24 de febrero de 2020, pero su legado nunca será olvidado.

Fuentes:

https://www.nasa.gov/content/katherine-johnson-biography

https://www.britannica.com/biography/Katherine-Johnson-mathematician

Pierre-Simon Laplace

Pierre-Simon Laplace fue un matemático y astrónomo francés que nació el 23 de marzo de 1749 y murió el 5 de marzo de 1827, sin el cual la astronomía matemática y la estadística no estarían ni cerca de estar tan avanzadas como lo están hoy. A menudo se le llama el Newton de Francia. Escribió un resumen de cinco volúmenes de su obra llamado Mécanique Céleste desde 1799 hasta 1825.

Fue enviado a la Universidad de Caen por su padre para leer teología cuando tuvo la edad suficiente. No se graduó en teología, sino que se fue a París cuando dos entusiastas profesores de matemáticas lo animaron a seguir sus pasos. Impresionando a d'Alembert por ser capaz de resolver rápidamente problemas matemáticos difíciles, se le aseguró un puesto en la école Militaire. Asegurado con dinero, comenzó entonces su investigación.

Tiene muchos nombres en su honor: la ecuación de Laplace, la transformada de Laplace y el operador diferencial laplaciano, por nombrar algunos. También fue uno de los primeros científicos en sugerir que los agujeros negros existen. Ascendió a conde en 1806 y fue nombrado marqués en 1817, estando casado y teniendo hijos.

Fuentes:

http://www-history.mcs.st-and.ac.uk/Biographies/Laplace.html

http://en.wikipedia.org/wiki/Pierre-Simon_Laplace

Gottfried Leibniz

Gottfried Leibniz fue un matemático y filósofo alemán, nacido el 1 de julio de 1646. Ocupa un lugar destacado en la historia de las matemáticas y la filosofía. Era hijo de Friedrich Leibniz, profesor de filosofía moral en Leipzig. La madre de Leibniz era Catharina Schmuck, hija de un abogado y tercera esposa de Friedrich Leibniz. Sin embargo, Friedrich Leibniz murió cuando Leibniz tenía solo seis años y fue criado por su madre.

A la edad de siete años, Leibniz ingresó en la Escuela Nicolai de Leipzig. Aunque le enseñaron latín en la escuela, Leibniz había aprendido por sí mismo latín mucho más avanzado y algo de griego a la edad de 12 años, impulsado por su interés en leer los libros de su padre. A medida que avanzaba en la escuela, le enseñaron la lógica y la teoría de Aristóteles para categorizar el conocimiento. Leibniz claramente no estaba satisfecho con el sistema de Aristóteles y comenzó a desarrollar sus propias ideas sobre cómo mejorarlo. Más tarde en su vida, Leibniz recuerda que en ese momento estaba tratando de encontrar un orden a las verdades lógicas que, aunque no lo sabía en ese momento, eran las ideas detrás de las rigurosas demostraciones matemáticas. Además de sus tareas escolares, Leibniz estudió los libros de su padre. En particular, leyó libros de metafísica y libros de teología de escritores católicos y protestantes. Leibniz desarrolló el cálculo infinitesimal independientemente de Isaac Newton, y se convirtió en uno de los inventores más prolíficos en el campo de las calculadoras mecánicas. Leibniz también es conocido por refinar el sistema numérico binario, que es la base de prácticamente todas las computadoras digitales. Murió el 14 de noviembre de 1716.

Fuentes:

http://www.businessinsider.com/important-mathematicians-modern-world-2012-7?op=1

http://www-history.mcs.st-andrews.ac.uk/Biographies/Leibniz.html

Liu Hui

Liu Hui fue un matemático chino que vivió en el estado de Cao Wei durante el período de los Tres Reinos (220-280) de China. En 263, escribió un libro con soluciones a problemas presentados en el famoso libro chino de matemáticas, "Los Nueve Capítulos sobre el Arte Matemático". En este libro, fue posiblemente el primer matemático en descubrir, comprender y utilizar los números negativos, sin duda antes que el matemático indio Brahmagupta. En sus comentarios a los Nueve Capítulos, presentó: Un algoritmo para el cálculo de π (pi), la eliminación gaussiana, el principio de Cavalieri para encontrar el volumen de un cilindro y la intersección de dos cilindros perpendiculares.

Fuentes:

https://lifethroughamathematicianseyes.wordpress.com/2015/01/17/the-sea-island-mathematical-manual/

Ada Lovelace

Ada Lovelace, nacida el 10 de diciembre de 1815, fue una matemática y escritora inglesa. Trabajó en la Máquina Analítica de Charles Babbage (una de las primeras computadoras mecánicas de propósito general). Una de sus Notas sobre la máquina analítica fue el primer algoritmo destinado a ser procesado por una computadora: ¡fue la primera programadora de computadoras del mundo! También es conocida como la primera persona que tuvo una visión de las computadoras que iba más allá de los cálculos aritméticos. Ada se interesó por primera vez en las matemáticas cuando creyó que le evitarían volverse "loca" como su padre, aunque cuando murió en 1852, pidió ser enterrada junto a él de todos modos.

Fuentes:

http://inventors.about.com/od/lstartinventors/p/Ada_Lovelace.htm

https://en.wikipedia.org/wiki/Ada_Lovelace

Sir Isaac Newton

Sir Isaac Newton fue un físico y matemático inglés nacido el 4 de enero de 1643 en Woolsthorpe, Lincolnshire. Ha sido ampliamente considerado como uno de los científicos más influyentes de todos los tiempos y como una figura clave en la revolución científica. Newton formuló las leyes del movimiento y la gravitación, construyó el primer telescopio reflector práctico, formuló una ley empírica de enfriamiento y estudió la velocidad de la luz. También hizo contribuciones a la óptica y comparte crédito con Gottfried Leibniz por la invención del cálculo infinitesimal.

Con mucho, la historia más famosa de Newton es cuando desarrolló la ley de la gravedad. El joven Isaac Newton se interesó por primera vez en la fuerza de la gravedad un día mientras estaba sentado en contemplación bajo un manzano y de repente fue golpeado en la cabeza por una manzana que caía. El incidente dejó a Newton con un dolor de cráneo y una idea notable: ¿qué pasaría si la gravedad, la fuerza que arrancaba las manzanas de los árboles, llegara realmente tan alto como la luna? A partir de aquí, hubo un pequeño salto al concepto de que la gravedad de la Tierra era responsable de mantener a la Luna en órbita y que la gravedad del Sol era responsable de mantener a los planetas en órbita.

En 1687 Newton publicó su libro Philosophiæ Naturalis Principa Mathematica "Principios matemáticos de la filosofía natural", donde sentó las bases de la mayor parte de la mecánica clásica y donde reveló al público su ley de la gravitación universal. Newton murió el 20 de marzo de 1727.

Fuentes:

Burton, D.M. La historia de las matemáticas: una introducción, 5ª ed.; McGraw-Hill: Nueva York, 2003.

http://www.newton.ac.uk/newtlife.html

http://www.bbc.co.uk/history/historic_figures/newton_isaac.shtml

http://www.dctech.com/eureka/short-stories/newton.php

http://en.wikipedia.org/wiki/Isaac_Newton

Emmy Noether

Emmy Noether, nacida en 1882, fue una matemática alemana conocida por sus increíbles contribuciones al álgebra abstracta y la física teórica. Fue descrita como la mujer más importante en matemáticas, ya que transformó las teorías de álgebras, anillos y campos.

Inicialmente iba a enseñar inglés y francés ya que estaba cualificada, pero estudió matemáticas donde su padre matemático enseñaba en la Universidad de Erlangen. En 1915, se unió al departamento de matemáticas de la Universidad de Göttingen. Noether se mudó a los Estados Unidos para trabajar en el Bryn Mawr College en Pensilvania cuando fue despedida de su puesto universitario por ser judía. Murió en 1935, cuatro días después de ser operada de un quiste ovárico.

Fuentes:

Musser, Gary. Hamburguesa, Guillermo. Peterson, Blake. Matemáticas para profesores de primaria: un enfoque contemporáneo, 6ª ed.; Wiley.

https://en.wikipedia.org/wiki/Emmy_Noether

Blaise Pascal

Blaise Pascal nació el 19 de junio de 1623 en Clermont-Ferrand, Francia. Pascal fue un matemático, físico, inventor, escritor y filósofo cristiano francés. Fue un niño prodigio que fue educado por su padre, un recaudador de impuestos, en Rouen. Los primeros trabajos de Pascal se centraron en las ciencias naturales aplicadas, donde realizó importantes contribuciones al estudio de los fluidos.

En 1642, a la edad de 18 años, inspirado por la idea de facilitar el trabajo de su padre de calcular impuestos, Pascal inventó la pascalina, que es una de las primeras calculadoras. La pascalina era una calculadora de rueda numérica con ocho esferas móviles, cada una de las cuales representaba un dígito numérico, como unos, decenas y centenas. La calculadora de pascalina era competente en realizar operaciones simples como la suma, la resta, la multiplicación y la división.

Pascal continuó influyendo en las matemáticas a lo largo de su vida. En 1653, su Traité du triangle arithmétique-Tratado sobre el triángulo aritmético se utilizó como una presentación eficiente para los coeficientes binomiales, y ahora se conoce como el triángulo de Pascal. Inicialmente, Pascal leyó sobre este triángulo en un libro chino. Lo estudió rigurosamente, y se le atribuye el honor de que este triángulo esté en su nombre.

Pascal luchó contra el insomnio y un doloroso trastorno digestivo llamado dispepsia desde que era adolescente y, a lo largo de los años, el trabajo constante de Pascal afectó su ya frágil salud.

Pascal murió de un tumor estomacal maligno el 19 de agosto de 1662. Para entonces, el tumor se había extendido a su cerebro. Tenía 39 años en el momento de su muerte.

Fuentes:

http://www-history.mcs.st-andrews.ac.uk/Mathematicians/Pascal.html

Conway, John. Guy, Richard. El libro de los números. Libros de Copérnico.

http://en.wikipedia.org/wiki/Blaise_Pascal

Platón

Platón nació en el seno de una familia acomodada y fue alumno del gran filósofo Sócrates. Nació en Atenas, Grecia, en el año 428 a.C., y es considerado uno de los filósofos griegos más importantes de la historia. Platón fundó la Academia de Atenas, una institución dedicada a la investigación y la enseñanza de la filosofía y las ciencias. De hecho, el cartel sobre la entrada de la Academia decía "Que nadie que ignore la geometría entre aquí". Allí, los estudiantes se centraron en preguntas importantes como "¿Qué es el yo?" y "¿Cuál es la naturaleza humana?". Aristóteles no solo fue el primer alumno de Platón, sino también uno de sus mejores. Sus trabajos sobre filosofía, política y matemáticas fueron muy influyentes y sentaron las bases del enfoque sistemático de Euclides hacia las matemáticas.

Platón estudió el estatus ontológico (categorías del ser) de los objetos matemáticos. Es más conocido por su identificación de los llamados sólidos platónicos: el tetraedro simétrico y tridimensional, el cubo, el octaedro, el dodecaedro y el icosaedro.

Fuentes:

Burton, D.M. La historia de las matemáticas: una introducción, 5ª ed.; McGraw-Hill: Nueva York, 2003.

http://www.ourcivilisation.com/smartboard/shop/warnerr/plato.htm

http://www.storyofmathematics.com/greek_plato.html

Pitágoras de Samos

Pitágoras fue un matemático griego nacido entre los años 580 y 569 a.C. en la isla egea de Samos. Nuestro conocimiento de la vida de Pitágoras es escaso, y poco se puede decir con certeza. La información conocida hasta la fecha sobre Pitágoras se ha filtrado a partir de los primeros escritores que compitieron entre sí en la invención de fábulas sobre sus viajes, poderes milagrosos y enseñanzas. Pitágoras fundó una escuela en el sur de Italia; Esta escuela, considerada una academia de filosofía, matemáticas y ciencias naturales, se convirtió en una hermandad estrechamente entrelazada con ritos y observancias secretas. La escuela trató de regular estrictamente la dieta y el modo de vida de sus miembros, e imponer un método común de educación. Los estudiantes de esta escuela se concentraban en cuatro materias de estudio: aritmética, geometría, música y astronomía. Cuando Pitágoras tenía unos 60 años, se casó con una de sus alumnas, Theano. Fue una matemática notablemente hábil que inspiró a Pitágoras durante los últimos años de su vida, y también contribuyó a transmitir su sistema de enseñanza después de su muerte. Mucho después de la muerte de Pitágoras en el año 500 a.C., la hermandad continuó existiendo durante al menos dos siglos más. Los pitagóricos tenían extrañas iniciaciones, ritos y prohibiciones. Por ejemplo, se negaban a comer frijoles, beber vino y recoger cualquier cosa que hubiera caído, o avivar el fuego con una plancha. Insistían, además de estos curiosos tabúes, en una vida de virtud, especialmente de amistad. La estrella de cinco puntas, o pentagrama, se utilizaba como signo por el cual los miembros de la hermandad podían reconocerse entre sí.

Pitágoras es bien conocido por su contribución en el área de la geometría, y se le ha acreditado el Teorema de Pitágoras dentro de la geometría. Este teorema establece que en un triángulo rectángulo el área del cuadrado en la hipotenusa (el lado más largo de un triángulo rectángulo) es igual a la suma de las áreas de los cuadrados de los otros dos lados, es decir, c² = a² + b².

Fuentes:

Burton, D.M. La historia de las matemáticas: una introducción, 5ª ed.; McGraw-Hill: Nueva York, 2003.

Musser, Gary. Hamburguesa, Guillermo. Peterson, Blake. Matemáticas para profesores de primaria: un enfoque contemporáneo, 6ª ed.; Wiley.

http://www-groups.dcs.st-and.ac.uk/history/Biographies/Pythagoras.html

http://en.wikipedia.org/wiki/Pythagoras

Alan Turing

Alan Turing, nacido el 23 de junio de 1912, fue un matemático, lógico, criptoanalista y científico informático británico. Dio definiciones de los conceptos de algoritmo y computación con su máquina de Turing, que es esencialmente un modelo de computadora. También fue responsable de descodificar mensajes alemanes durante la Segunda Guerra Mundial. Después de la Segunda Guerra Mundial, diseñó el ACE en el Laboratorio Nacional de Física, que es una computadora con programa almacenado. Luego ayudó a desarrollar las computadoras de Manchester en la Universidad de Manchester, lo que finalmente lo llevó a fascinarse por la biología matemática, escribiendo varios artículos sobre este tema. Su homosexualidad lo llevó a ser procesado en el Reino Unido en 1952. Aceptó que le inyectaran hormonas femeninas en lugar de ir a la cárcel. Murió el 7 de junio de 1954 debido a un envenenamiento por cianuro. Hasta la fecha, se desconoce si fue un suicidio o un accidente. Sin embargo, lo encontraron muerto con una manzana a medio comer a su lado, y era un gran fan de Blancanieves y los siete enanitos... no hace falta decir más.

Fuentes:

http://www.alanturing.net/

http://en.wikipedia.org/wiki/Alan_Turing

Zu Chongzhi

Zu Chongzhi (429-500 d.C.), nombre de cortesía Wenyuan, fue un matemático, astrónomo, escritor y político chino durante las dinastías Liu Song y Qi del Sur.

Uno de sus logros más famosos es derivar dos aproximaciones de pi, (3.1415926535897932...) que se mantuvo como la aproximación más precisa para π durante más de novecientos años. Su mejor aproximación estuvo entre 3.1415926 y 3.1415927, con 355/113 (密率, relación cercana) y 22/7 (約率, relación aproximada) siendo las otras aproximaciones notables. Obtuvo el resultado aproximando un círculo con un polígono de 24.576 (= 213 × 3) lados. Esta fue una hazaña impresionante para la época, especialmente teniendo en cuenta que el dispositivo de conteo de varillas que utilizó para registrar los resultados intermedios era simplemente una pila de palos de madera dispuestos en ciertos patrones.

Fuentes:

https://en.wikipedia.org/wiki/Zu_Chongzhi